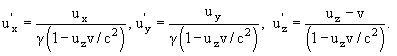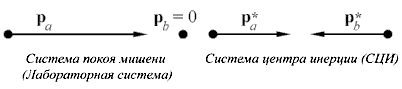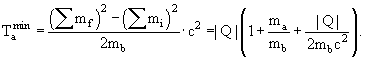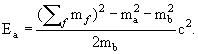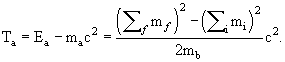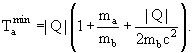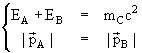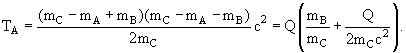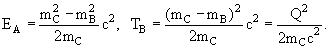Семинар 1. Введение. Физика микромира

• Теория относительности, изменившая существующие в классической физике представления о пространстве и времени.
• Квантовая теория, изменившая представление о структуре материи. Явление радиоактивности, открытие электрона, сложная структура атома, протон-нейтронная структура атомного ядра, открытие фундаментальных частиц и взаимодействий привели к современному представлению об окружающем мире.
• Открытия в области физики частиц, коренным образом повлиявшие на понимание процессов, происходящих во Вселенной.

1.1.     Масштабы явлений в физике

1.2.     Упругое рассеяние α-частиц. Формула Резерфорда

1.3.     Сечение реакции

1.4.     Размер ядра

1.5.     Радиоактивность

1.6.     Преобразования Лоренца

1.7.     Эффект Доплера

1.8.     Системы отсчета

1.9.     Основные формулы релятивистской физики

1.10.   Система единиц Гаусса

1.11.   Энергия и порог реакции

1.12.   Энергии частиц в двухчастичном распаде

           Задачи

1.1. Масштабы явлений в физике

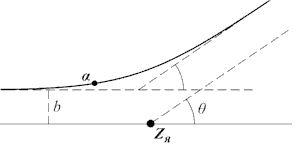
1.2. Упругое рассеяние α-частиц. Формула Резерфорда

    Классическая физика основана на ряде блестящих экспериментов, среди которых особое место занимают эксперименты Г. Кавендиша и Ш. Кулона. С помощью крутильных весов ими были установлены законы гравитационного и электрического взаимодействий макроскопических тел. Однако метод эксперимента, который использовался Кавендишем и Кулоном, не может использоваться в микрофизике из-за малых размеров исследуемых объектов.
    Новый метод изучения микроскопических систем, был предложен Э. Резерфордом. Он первым разработал и применил метод исследования с помощью рассеяния пробной «частицы-снаряда» на исследуемом объекте. В своем первом эксперименте Резерфорд использовал рассеяние α-частиц на атомах для того, чтобы изучить атомную структуру. Выяснив, что вероятность рассеяния α-частиц на атоме, как функция угла рассеяния θ, подчиняется формуле Резерфорда для рассеяния ее на точечном кулоновском центре

вероятность рассеяния ~ ,

(1.1)

где Z_α, Z_я – заряды (в единицах элементарного заряда) α-частицы и ядра-мишени, Т – кинетическая энергия α-частицы, он установил, что в атоме имеется ядро размером менее 5·10^–12 см, сосредотачивающее в себе почти всю массу атома.

Рис. 1.1 Рассеяние α-частицы на ядре мишени с зарядом Zя. Угол рассеяния θ зависит от прицельного параметра b: tg(θ/2) = ZαZяe2/(2bT).

1.3. Сечение реакции

    Для характеристики вероятности процессов в микромире пользуются понятиями полного эффективного сечения σ и дифференциального эффективного сечения dσ/dΩ. Дифференциальное сечение используется для описания вероятности процесса взаимодействия частиц. Если мишень содержит N_М ядер и вся находится в пучке падающих частиц плотностью
j (j - число частиц, падающих в единицу времени на единицу поперечной площади мишени), то число dN(0)/dΩ частиц, рассеиваемых мишенью в единицу времени на угол θ в пределах телесного угла dΩ, определяется соотношением:

(1.2)

Полное число частиц, рассеиваемых мишенью в единицу времени под всеми углами, определяется соотношением

(1.3)

σ − полное эффективное сечение, N_М = nSd − характеристика мишени (n − число ядер мишени в единице объёма, S − облучаемая поперечная площадь мишени, d − толщина мишени в направлении падающего пучка частиц). Полное сечение измеряется в барнах (1 барн = 10^–24см²).

1.4. Размер ядра

    Наиболее распространенный метод исследования атомных ядер – это рассеяние на ядрах различных частиц и ядер, ускоренных до высоких энергий. Точные данные по размерам атомных ядер были получены из экспериментов по рассеянию электронов. Радиусы ядер R растут с увеличением массового числа А и хорошо описываются соотношением

Численный коэффициент в (1.4) зависит от методики определения радиуса ядра и меняется в пределах 1.1÷1.4. Здесь и далее будет использоваться значение 1.3.

1.5. Радиоактивность

    Радиоактивность – свойство атомных ядер самопроизвольно (спонтанно) изменять свой состав (заряд Z, массовое число A) в результате испускания частиц или ядерных фрагментов. К явлению радиоактивности относится также испускание атомным ядром гамма-квантов, но при этом ни заряд Z, ни массовое число A не изменяются.

Рис. 1.2. Зависимость активности от времени (слева). Данная зависимость в логарифмическом масштабе отображается прямой, тангенс угла наклона которой равен постоянной распада λ. Справа приведена кривая активации (наведенной радиоактивности) в зависимости от времени. Рост числа радиоактивных ядер практически прекращается при достижении активации насыщения за время t ≈ 5T_1/2

    Процесс радиоактивного распада, как и все процессы в микромире, – это случайный (статистический) процесс. Атомные ядра одного сорта распадаются за разное время. Однако среднее время жизни τ ядер, вычисленное по наблюдению большого числа распадов, оказывается не зависящим от способа получения этих ядер и от внешних условий. Среднее время жизни τ ядра характеризует скорость их распада. Постоянная распада λ:

Физический смысл λ – это вероятность распада радиоактивного ядра в единицу времени.
    Закон радиоактивного распада показывает, как со временем изменяется в среднем число радиоактивных ядер в образце. Если в момент времени t имеется большое число N радиоактивных ядер, то к моменту t + dt распад испытают в среднем λNdt ядер. Поэтому изменение их числа dN определяется соотношением

Знак минус означает, что общее число радиоактивных ядер (частиц) уменьшается в процессе распада. Интегрируя соотношение (1.6), получим закон радиоактивного распада:

где N₀ − число радиоактивных ядер в начальный момент t = 0. Закон радиоактивного распада относится к статистическим средним и справедлив лишь при достаточно большом числе распадающихся ядер.
    Среднее время жизни τ ядра вычисляется по формуле

.

(1.8)

    Часто для характеристики скорости радиоактивного распада атомных ядер используют величину, называемую периодом полураспада – T_1/2. Период полураспада – это время, за которое число радиоактивных ядер уменьшается вдвое:  N₀/2 = N₀, откуда

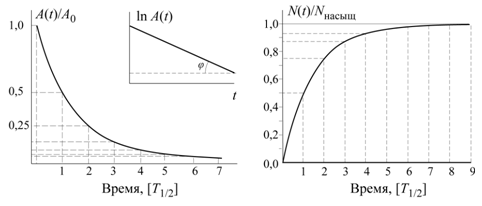
    Активность образца А – число распадов в единицу времени, является производной от N по времени, взятой с обратным знаком:

Активность образца уменьшается со временем по тому же экспоненциаль­ному закону, что и число нестабильных ядер. Активность измеряют в беккерелях или в кюри.

    Энергия распадающейся системы в соответствии с принципом неопределенностей Гейзенберга, не может быть точно определена. Всякое распадающееся состояние, имеющее среднее время жизни τ, описывается волновой функцией ψ(t), квадрат модуля которой убывает со временем по экспоненциальному закону радиоактивного распада

|ψ(t)|² = |ψ(0)|²e^-t/τ.

Ядро в любом состоянии с τ ≠ ∞ имеет энергетическую неопределённость ΔE ≈ Г, которая связана с τ соотношением неопределённостей Г·τ ≈ ћ , где Г – ширина уровня на половине высоты.
    Подавляющее число частиц также являются нестабильными и распадаются по тем же законам радиоактивного распада, как и атомные ядра. Традиционно радиоактивность атомных ядер описывают, используя период полураспада T_1/2, а распады частиц описывают, использую среднее время жизни τ

1.6. Преобразования Лоренца

    Основные положения специальной теории относительности изучались в разделе «Механика» общего курса физики. Здесь лишь напомним основные соотношения релятивистской физики.

Рис. 1.3. Штрихованная система S' движется относительно системы S со скоростью вдоль оси z.

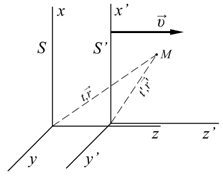
    Рассмотрим материальную точку с массой покоя m. Ее координаты в инерциальной системе отсчета S определяются как (t,) = (t,x,y,z), а скорость v = ||. Координаты той же точки в другой инерциальной системе отсчета S' (t',x',y',z'), движущейся относительно S вдоль оси z с постоянной скоростью , связаны с координатами в системе S преобразованиями Лоренца. В случае, если координатные оси систем z и z' сонаправлены с вектором и в начальный момент времени t = t' = 0 начала координат обеих систем совпадали, то преобразования Лоренца даются выражениями:

где β = v/c  (0 < β < 1), а  γ = 1/(1 – β²)^1/2 – лоренц-фактор.

Скорость частицы ' в системе S' связана со скоростью в системе S соотношением:

(1.12)

Обратные преобразования Лоренца получаются взаимной заменой координат r_i → r_i', v_i  → v_i' и учетом изменения направления скорости v → -v:

При малых скоростях преобразования Лоренца совпадают с выражениями для нерелятивистских преобразований Галилея:

Относительность пространственных расстояний (Сокращение Лоренца-Фитцджеральда):

Относительность промежутков времени между событиями  (релятивистское замедление времени):

Относительность одновременности событий. Если в системе S для событий A и B t_A = t_B и x_A ≠ x_B, то в системе S'

    В общем случае преобразования Лоренца записываются в терминах
4-векторов a = (a⁰,) = (a⁰,a¹,a²,a³). При относительном движении систем S и S', как на рис. 1.2, 4-вектор a преобразуется следующим образом:

Таким образом, квадрат 4-вектора также является инвариантом. Например, квадрат 4-вектора координаты

(X)2 = (ct,)2 = c2t2 − ()2 = τ2

(1.18)

определяет "собственное" время частицы (т.е. время в ее системе отсчета). 4-вектор скорости
u = γ(c,) вводится таким образом, чтобы (u)² = c². 4-импульс, определяется как произведение массы на скорость

P = mu = mγ(c,) = (E/c,).

(1.19)

Так как u² = c², то (P)² = m²c² = (E/c)² − ()², или

Следовательно,

E = γmc2, = γm, = c2/E.

(1.21)

Преобразования Лоренца для 4-импульса (1.17):

Скалярное произведение 4-импульсов является инвариантом по определению. Вместо произведения 4-импульсов двух частиц, например P₁P₂, обычно используют квадрат инвариантной массы двух частиц (s-инвариант):

(1.23)

или квадрат переданного импульса (t-инвариант)

1.7. Эффект Доплера

    Если в системе S (рис. 1.2) в направлении оси z испущен фотон энергии E₀ = p₀c, то его энергия E, длина волны λ и частота ν в системе отсчета S' (наблюдатель удаляется от источника света) составит

E = γ(E₀ − βp₀c) = γE₀(1 − β),

(1.24)

Параметр смещения z в этом случае z = (λ − λ₀)/λ₀ = (ν₀ − )/ν > 0, что соответствует красному смещению λ > λ₀, ν < ν₀. Если скорость системы S' направлена в противоположную сторону (наблюдатель приближается к источнику света), то знаки изменяются на противоположные:

(1.25)

В данном случае наблюдается синее смещение: λ < λ₀. Поскольку в общем случае преобразование Лоренца записывается как E = γ(E₀ − ()/c², то, в отличие от классической физики, в релятивистском случае наблюдается поперечный эффект Доплера: v/v₀ = γ.
    Из формул, соответствующих синему смещению, можно получить классическую формулировку эффекта Доплера, используя разложение в ряд:

Тогда для относительного изменения частоты излучения: Δν/ν₀ = β = v/c, что соответствует классической формулировке эффекта Доплера (без учета среды):

ν = ν₀(1 + ν/ν_звук).

1.8. Системы отсчета

    Рассмотрим двухчастичный процесс a + b → c + d. 4-х импульсы сталкивающихся частиц
P_a = (E_a/c,_a) и P_b = (E_b/c,_b) соответственно.
    При описании взаимодействий частиц и атомных ядер, как и в классической физике, обычно используются две системы отсчета: система покоя мишени и система центра инерции (рис. 1.4).

Рис. 1.4. Определение некоторых систем отсчета

1. Система покоя мишени – система, в которой частица b (мишень) покоится, p_b = 0, E_b =  m_bc². Обычно под лабораторной системой (ЛС) отсчета подразумевается система покоя мишени. В данной системе s-инвариант:

(1.26)

Энергия налетающей частицы, выраженная через s-инвариант:

(1.27)

2. Система центра инерции (СЦИ) – система, в которой ^*_a = ^*_b = 0. Величины в СЦИ в дальнейшем будут отмечаться звездочкой. В СЦИ . s-инвариант в СЦИ:

(1.28)

В экспериментах физики высоких энергий часто используется система встречных пучков – система, в которой частицы равной массы и равных по абсолютной величине импульсов сталкиваются под углом π − θ. При θ = 0 система встречных пучков совпадает с СЦИ.

1.9. Основные формулы релятивистской физики

    Универсальность законов сохранения приводит к необходимости установить для релятивистской кинематики такие уравнения, которые удовлетворяли бы к законам сохранения энергии и импульса и были инвариантны относительно преобразований Лоренца:

1. E = (m²c⁴ + p²c²)^1/2 = γmc² = mc² + T,
   E – полная энергия частицы, m – масса частицы,
   с – скорость света в вакууме,
   = γm – релятивистский импульс частицы,
   β = v/c, γ = (1 – β²)^-1/2 – Лоренц-фактор, – скорость частицы,
   T = mc²(γ – 1) – релятивистская кинетическая энергия частицы.
2. p²c² = T(2mc² + T).
3. τ = γτ₀ – релятивистское замедление времени,
   τ₀ – время жизни частицы в состоянии покоя,
   τ – времени жизни частицы, движущейся со скоростью .
4. l = l₀/γ,
5. E² – p²c² = inv = m²c⁴,
   E – полная энергия частицы или системы частиц,
   p – импульс частицы или суммарный импульс системы частиц.
6. Энергия налетающих частиц Е в ускорителе с неподвижной мишенью, эквивалентном коллайдеру с пучками частиц массы m и энергии E*:

   (1.29)

7. Порог реакции. Если на неподвижной мишени b под действием налетающих частиц a происходит реакция a + b → c + d +... и энергия реакции (изменение суммарной массы частиц) Q = (∑m_i – ∑m_f)c² < 0, то минимальная кинетическая энергия частицы а, необходимая для осуществления такой реакции

   (1.30)

1.10. Система единиц Гаусса

    При решении задач будет использоваться система единиц Гаусса, в которой основными единицами являются сантиметр, грамм и секунда. В данной системе диэлектрическая и магнитная проницаемости являются безразмерными величинами, причём для вакуума они приняты равными единице. В качестве единицы измерения энергии используется внесистемная единица 1 эВ (электрон-Вольт) – энергия, приобретаемая электроном при прохождении потенциала в 1 Вольт.

1.11. Энергия и порог реакции

Пороговая энергия реакции – это дополнительная кинетическая энергия, необходимая для осуществления эндотермической реакции (Q < 0). Данное значение энергии соответствует предельному случаю, когда продукты реакции образуются с нулевыми импульсами в СЦИ и s-инвариант в конечном состоянии равен квадрату суммы масс конечных продуктов: . В начальном состоянии в СЦИ . Следовательно, необходимая суммарная энергия сталкивающихся частиц должна быть .
    Пороговая кинетическая энергия в СЦИ:

    В лабораторной системе отсчета частица-мишень покоится: |_b| = 0, E_b = m_bc². Соответственно, s-инвариант в лабораторной системе в начальном состоянии равен:

Приравнивая s в начальном и конечном состояниях, получаем:

(1.32)

(1.33)

Раскладывая разность квадратов и выделяя Q, получим (1.31):

(1.34)

    Значение пороговой энергии реакции в лабораторной системе всегда больше соответствующего значения в системе центра инерции. Их разность определяет ту часть энергии, которая идет на движение центра инерции в лабораторной системе.

1.12. Энергии частиц в двухчастичном распаде

Учитывая, что (pc)² = E² − (mc²)² и подставляя выражение E_B через E_A во второе уравнение, получим:

E²_A − (m_Ac²)² = (m_Сc² −  E_A)² − (m_Bc²)².

Отсюда для частицы A:

(1.35)

Выражения для частицы B получаются перестановкой соответствующих индексов.
    Полезно выписать выражения для энергий продуктов распада в некоторых частных случаях:
а) распад на частицы равной массы m_A = m_B.

(1.36)

б) образование безмассовой частицы m_A = 0.

(1.37)

в) нерелятивистский случай: Q << m_Cc², m_C ≈ m_A + m_B

(1.38)

Задачи

1.1. Альфа-частица (Z_α = 2) с кинетической энергией T = 5 МэВ испытывает лобовое столкновение с ядром золота (Z_я = 79). Рассчитать расстояние максимального сближения α-частицы с ядром золота.

1.2. Протон с кинетической энергией Т = 2 МэВ налетает на неподвижное ядро ¹⁹⁷Au. Определить дифференциальное сечение рассеяния dσ/dΩ на угол θ = 60° . Как изменится величина дифференциального сечения рассеяния, если в качестве рассеивающего ядра выбрать ²⁷Al?

1.3. Частица массы m_a налетает на покоящуюся частицу массы m_b. В результате реакции в конечном состоянии образуется n частиц с массами m'₁,…m'_n. Определить энергию и порог реакции.

    Обозначим суммарную массу взаимодействующих частиц m_a + m_b = ∑_im_i  (индекс i соответствует начальному состоянию (initial)),  суммарную массу образовавшихся частиц
m'₁ + m'₂ + ...+ m'_n = ∑_f m_f  (индекс f обозначает конечное состояние (final)). Энергия реакции Q соответствует изменению суммарной массы частиц:

    Пороговая энергия реакции – это дополнительная кинетическая энергия, необходимая для осуществления эндотермической реакции (Q < 0). Данное значение энергии соответствует предельному случаю, когда продукты реакции в СЦИ образуются с нулевыми импульсами и s-инвариант в конечном состоянии равен квадрату суммы масс конечных продуктов:
s = (∑_f P_f )/c² = (∑_fm_f ). В начальном состоянии в СЦИ s = (∑_i P*_i )/c² = (E*_a + E*_b)²/c⁴. Следовательно, необходимая суммарная энергия сталкивающихся частиц должна быть E*_a + E*_b = ∑_fm_f c².
    Пороговая кинетическая энергия в СЦИ:

T*_a +T*_b = ∑_fm_f c² − ∑_im_ic² = |Q|.

    В лабораторной системе отсчета частица-мишень покоится: |_b| = 0, E_b = m_bc². Соответственно, s-инвариант в лабораторной системе в начальном состоянии равен:

s = (P_a + P_b)/c² = (E_a/c² + E_b/c²) − (_a/c − _b/c)² = m_a² + m_b2 − 2E_am_b/c².

Приравнивая s в начальном и конечном состояниях, получаем:

(1.32)

(1.33)

Раскладывая разность квадратов и выделяя Q, получим (1.30):

(1.30)

    Значение пороговой энергии реакции в лабораторной системе всегда больше соответствующего значения в системе центра инерции. Их разность определяет ту часть энергии, которая идет на движение центра инерции в лабораторной системе.

1.4. Получим выражение для энергий и импульсов продуктов распада C → A + B через массы частиц в релятивистском случае в СЦИ.
    СЦИ связана с распадающейся частицей С, ее энергия в данной системе E_С = m_Сc², продукты распада разлетаются под углом 180°. Законы сохранения энергии и импульса:

Учитывая, что (pc)² = E² − (mc²)² и подставляя выражение E_B через E_A во второе уравнение, получим:

E²_A − (m_Ac²)² = (m_Сc² −  E_A)² − (m_Bc²)².

Отсюда для частицы A:

(1.35)

Выражения для частицы B получаются перестановкой соответствующих индексов.
    Полезно выписать выражения для энергий продуктов распада в некоторых частных случаях:
а) распад на частицы равной массы m_A = m_B.

(1.36)

б) образование безмассовой частицы m_A = 0.

(1.37)

в) нерелятивистский случай: Q << m_Cc², m_C ≈ m_A + m_B

(1.38)

1.5. Рассчитать кинетические энергии α-частицы и ядра ²²²Rn, образующихся при распаде
²²⁶Ra → ²²²Rn + α.
(m_Rn = 206764.10 МэВ, m_Ra = 210496.35 МэВ, m_α = 3727.38 МэВ.)
Ответ: Q_α = 4.87 МэВ, T_α = 4.78 МэВ, T_Rn = 0.086 МэВ

1.6. Рассчитать дифференциальное сечение рассеяния α-частицы с кинетической энергией 10 МэВ
1) на ядре кальция ⁴⁰Ca на угол 60°,
2) на ядре меди ⁶³Cu на угол 90°,
3) на ядре молибдена ⁹⁶Mo на угол 120°,
4) на ядре серебра ⁷⁹Ag на угол 180°.
Ответ: 1) 0.33 барн/стер, 2) 0.17 б/стер, 3) 0.16 б/стер, 4) 0.11 б/стер

1.7. Рассчитать отношение сечений рассеяния α-частиц с кинетической энергиями 10 МэВ на ядре ¹⁹⁷Au под углами 6° и 180°.
Ответ: W = 13.3·10⁴

1.8. Рассчитать расстояния максимального сближения R
1) α-частицы с кинетической энергией 5 МэВ с ядром ¹⁹⁷Au и ⁷Li,
2) α-частицы с кинетической энергией 10 МэВ с ядром ⁴⁰Ca,
3) протона с кинетической энергией 7 МэВ с ядром ¹⁹⁷Au,
4) α-частицы с кинетической энергией 5 МэВ с ядром ²⁰⁸Pb.
Ответ: 1) R = 1.7 Фм, 2) R = 5.8 Фм, 3) R = 16.2 Фм, 4) R = 47.2 Фм

1.9.Пучок α-частиц с энергией T_α = 5 МэВ падает перпендикулярно на фольгу из серебра толщиной 1 мг/см². α-частицы, рассеянные под углом 60°, регистрируются детектором площадью 1 см², расположенном на расстоянии 20 см от мишени. Какая доля от полного числа рассеянных α-частиц ΔN/N будет зарегистрирована детектором?
Ответ: ∆N(60º)/N = 4·10^–10

1.10. В ходе эксперимента медная фольга (Z = 29, M_mol = 63.55 г/моль) толщиной 2 мг/см² облучается пучком α-частиц с с кинетической энергией Т_α = 5 МэВ и интенсивностью 10⁵ частиц в секунду. Сколько α-частиц в минуту ∆N будет регистрировать детектор площадью 1 см², расположенный на расстоянии 10 см от мишени под следующими углами к направлению падающего пучка: 1) 30°, 2) 90°, 3) 120°?
Ответ: 1) ∆N(30º) ≈ 44 част., 2) ∆N(90º) ≈ 0.8 част., 3) ∆N(120º) ≈ 0.4 част.

1.11. Почему из экспериментов по упругому рассеянию α-частиц следовало, что в атоме расположено положительно заряженное атомное ядро размером < 5·10^–12 см? Почему полученные результаты нельзя было объяснить на основании модели Томсона?

1.12. Во сколько раз число распадов ядер радиоактивного изотопа йода ¹³¹I в течение первых суток больше числа распадов в течение вторых суток? Период полураспада изотопа  T_1/2(¹³¹I) = 193 часа.

1.13. Пучок π^–-мезонов движется со скоростью v = 0.9c. Среднее время жизни π^–-мезонов составляет τ = 2.6·10^–8 с. Какое расстояние в среднем они пройдут до своего распада?
Ответ: L_π = 16 м

1.14. На каком расстоянии интенсивность пучка мюонов с кинетической энергией T = 0.5 ГэВ, движущихся в вакууме, уменьшается до половины первоначального значения?
m_μ = 105.66 МэВ, τ_μ = 2.197·10^-6 сек.
Ответ: L  = 2.6 км

1.15. Полная энергия электрона составляет 2.5 МэВ. Определите его импульс и скорость в лабораторной системе отсчета.
Ответ: p = 2.45 МэВ/c, v = 0.989c

1.16. Электрон и протон ускоряются разностью потенциалов 10⁷ В. Рассчитайте фактор γ, скорость, импульс и полную энергию каждой частицы.
Ответ: 1) E ≈ pc = 10.5 МэВ, γ = 20.57, v = 0.999c; 2) E = 948.27 МэВ, pc = 137.35 МэВ, γ = 1.01, v = 0.147c

1.17. Какую энергию надо затратить, чтобы электрон достиг скорости а) 0.5 c, б) 0.9 c, в) 0.99 c.
Какая энергия необходима, чтобы протон достиг тех же скоростей?
Ответ: а) T_e = 0.08 МэВ, T_p = 145.2 МэВ; б) T_e = 0.66 МэВ, T_p = 1.2 ГэВ;
в) T_e = 3.11 МэВ, T_p = 5.7  ГэВ.

1.18. Какую энергию надо затратить, чтобы увеличить скорость протона а) от 0.20 c до 0.21 c,
б) от 0.80 c до 0.81 c, в) от 0.90 c до 0.91 c, г) от 0.98 c до 0.99 c.
Ответ: а) T_p = 2.05 МэВ, б) T_p = 36.2 МэВ, в) T_p = 110.5 МэВ, г) T_p = 1 936 МэВ

1.19. Полная энергия частицы в два раза больше ее энергии покоя. Рассчитайте отношение v/c для этой частицы и определите ее импульс.

1.20. Определите массу частицы если известно, что ее импульс равен 500 МэВ/c,
а энергия – 1746 МэВ.

1.21. Рассчитайте скорость уменьшения массы Солнца, если известно, что плотность лучистой энергии Солнца на Земле в среднем равна 1.37·10³ Вт/м².

1.22. Энергия связи электрона в атоме водорода составляет 13.6 эВ. Насколько масса атома водорода меньше суммы масс электрона и протона?

1.23. Энергия связи дейтрона (система, состоящая из протона и нейтрона) составляет 2.224 МэВ. Насколько масса ядра дейтрона меньше суммы масс составляющих его нуклонов?

1.24. Энергия, выделяющаяся при делении одного ядра ²³⁵U, составляет ~200 МэВ. Какое количество массы ядра урана превращается в энергию?

1.25. Какой должна быть относительная скорость двух наблюдателей, чтобы измеряемые ими интервалы времени различались на 5 %?
Ответ: υ = 0.33с

1.26. На какое время разойдутся показания часов земного наблюдателя и наблюдателя на спутнике Земли с периодом обращения 90 мин через 5 лет?
Ответ: ∆t = 0.05 с

1.27. Используя разложение в ряд, получите следующие формулы для приближенного вычисления релятивистских поправок в случае
v << c: ; ; .

1.28. Исходя из релятивистского соотношения между энергией и импульсом, покажите, что в нерелятивистском пределе выполняется соотношение для кинетической энергии T = mv²/2.

1.29. Длина волны, излучаемая атомом водорода, составляет λ₀ = 6560 Å. Измерение длины волны этого же излучения из удаляющейся галактики составляет λ₁ = 14580 Å. Определите скорость, с которой галактика удаляется от Земли.
Ответ: υ = 2·10⁸ м/с

1.30. Галактика удаляется от земного наблюдателя со скоростью 1.9·10⁷ м/с. Определите относительную величину красного смещения (λ₁ − λ₀)/λ₀ для света этой галактики.
Ответ: z = 0.065 ≈ β

1.31. Измерение гравитационного потенциала ∆φ при удалении на бесконечность с расстояния R от центра сферического не вращающегося тела массы M составляет При этом величина красного смещения света определяется соотношением . Оцените величину красного смещения линии водорода в гравитационном поле Солнца. Оцените величину синего смещения этой линии в гравитационном поле Земли.

1.32. Видимый свет от близкой звезды смещен в фиолетовую часть спектра на 5 %. С какой лучевой скоростью движется звезда?
Ответ: β = 0.05c, v = 1.5·10⁷ м/с

1.33. С какой скоростью должен двигаться автомобиль, чтобы красный свет светофора выглядел зеленым? Сравните результат с космическими скоростями.

1.34. Определить порог реакции α + α → ⁷Li + p. Определить долю кинетической энергии налетающей частицы, идущую на движение центра инерции. m_α = 3727.38 МэВ, m_p = 938.27 МэВ,
m_Li = 6533.83 МэВ.

1.35. Рассчитать порог реакции ¹⁴N + α → ¹⁷O + p в двух случаях:

• налетающей частицей является ядро азота ¹⁴N,
• налетающей частицей является α-частица.

Объяснить полученный результат.

1.36. 1) В коллайдере LHC энергия пучков протонов составляет E*_p = 7 ТэВ. Определите энергию столкновения √s в системе центра инерции. Какая энергия протонного пучка E_p потребовалась бы для достижения данной энергии в ускорителе с неподвижной мишенью? Сравните результат с энергией протонов космических лучей.
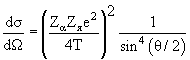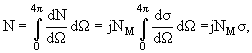
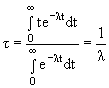2) В условии задачи 1) рассмотрите столкновение пучков электронов и позитронов с энергиями
E*_e = 500 ГэВ (проект ILC).
3) В условии задачи 1) рассмотрите столкновение пучков протонов с энергиями E*_p = 1 ТэВ (коллайдер TEVATRON).
4) В условии задачи 1) рассмотрите столкновение пучков электронов с энергиями E*_e =  100 ГэВ (коллайдер LEP)
Ответ: 1) E_p = 10⁸ ГэВ, 2) E_e = 10⁹ ГэВ, 3) E_p = 2·10⁶ ГэВ, 4) E_e = 4·10⁷ ГэВ

26.10.2016