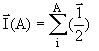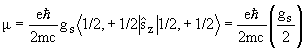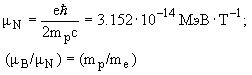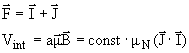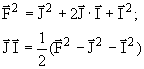2.5. Изоспин нуклонов и ядер

    Как основное, так и возбужденные состояния ядер - помимо рассмотренных на предыдущих семинарах энергии, спина и четности- характеризуются квантовыми числами, которые называются изоспином и проекцией изоспина.( В литературе эти квантовые числа обозначаются обычно либо символами T и T_z, либо I и I_z ).
    Введение этих квантовых чисел связано с тем фактом, что ядерные силы инвариантны относительно замены протонов на нейтроны. Это особенно ярко проявляется в спектрах т.н.”зеркальных” ядер, т.е. ядер-изобар, у которых число протонов одного равно числу нейтронов другого. (См., например, спектры ядер ¹³C и ¹³N). Для всех известных пар таких ядер имеет место подобие спектров низших возбужденных состояний: спины и четности низших состояний одинаковы, а энергии возбуждения близки.
    С точки зрения теории изоспина, нейтрон и протон являются одной и той же частицей - нуклоном с изоспином I = 1/2 - в двух разных состояниях, различающихся проекцией изоспина на выделенную ось (I_z = I₃) в пространстве изоспина. Таких проекций для момента I = 1/2 может быть только две: I_z = +1/2 (протон) и I_z = -1/2 (нейтрон). (Квантовая теория изоспина построена по аналогии с теорией спина. Однако пространство изоспина не совпадает с обычным координатным пространством.)
    Система Z протонов и N нейтронов - ядро - имеет проекцию изоспина

              Изоспин системы нуклонов является векторной суммой изоспинов составляющих:

    Ядерные (т.е.сильные) взаимодействия не зависят от проекции изоспина, или, точнее, сильные взаимодействия инвариантны относительно вращений в изоспиновом пространстве.
   Однако от величины изоспина ядерные силы зависят! Низшим по энергии состояниям системы нуклонов, т.е. основным состоянием ядра, является состояние с низшим возможным значением изоспина, которое равно

    Возбужденные состояния ядер могут иметь более высокие значения изоспина, но с той же проекцией.
Таким образом, характеристиками уровней данного ядра являются энергия, спин состояния, четность состояния и изоспин. Обычно три последних квантовых числа указываются как J^P, I

Ядро ⁴⁸Ca имеет 20 протонов и 28 нейтронов. Следовательно, проекция изоспина I_z этого ядра равна
I_z = (20 - 28) / 2 = - 4. Изоспин основного состояния I = |I_z | = 4.
Частицы или системы частиц, имеющие одинаковый изоспин и разные проекции изоспина, составляют изоспиновые мультиплеты (дублеты, триплеты, и т.д.). Особенностью членов такого мультиплета является то, что они одинаковым образом участвуют в сильном взаимодействии. Простейший пример дублета - нейтрон и протон. Состояния зеркальных ядер ¹³C и ¹³N являются другим примером (см. Спектры ядер.) 

2.6. Электромагнитные моменты нуклонов и ядер.

Электромагнитные моменты определяют потенциал взаимодействия ядра или частиц с внешними электрическими и магнитными полями:

Здесь Ze - заряд ядра, D - электрический дипольный момент ядра, Q -квадрупольный момент ядра, - магнитный дипольный момент. Более высокие по тензорной размерности члены потенциала взаимодействия (2.18) дают пренебрежимо малый вклад во взаимодействие.
   Электрический дипольный момент ядер в основном состоянии равен нулю (с точностью до малых членов, связанных со слабыми взаимодействиями в ядрах). Равенство нулю момента D_i является следствием четности квадрата волновой функции основного состояния ядра:

Квадрат волновой функции основного состояния ядра является четной функцией координат, z - нечетная функция. Интеграл по трехмерному пространству от произведения четной и нечетной функций всегда равен 0.
    Квадрат ψ-функции имеет положительную четность в случае, если сама ψ-функция имеет определенную четность(+ или -). Это справедливо для вкладов в ψ-функцию от сильных и электромагнитных взаимодействий, сохраняющих четность. Малые добавки в ψ-функцию от слабых ( не сохраняющих четность) взаимодействий могут дать отклонение от нуля для дипольных моментов ядер и частиц. Роль этих вкладов представляет большой интерес для современной физики, поэтому попытки измерить дипольный момент нейтрона не прекращаются.
   Квадрупольный электрический момент ядра в системе координат, связанной с ядром (внутренний квадрупольный момент)

Поскольку среднее значение физической величины в квантовой механике, по определению,

,

внутренний квадрупольный момент, с точностью до констант, есть разность среднего значения величины 2z² и среднего значения суммы квадратов x² и y². Поэтому для сферических ядер Q = 0, для вытянутых относительно внутренней оси вращения z Q > 0 , а для сплюснутых Q < 0.

    Магнитный дипольный момент частицы является оператором в пространстве волновых функций частиц и связан с операторами орбитального и спинового моментов соотношением

 Здесь m - масса частицы, e/2mc - магнетон.(В магнетоне Бора для электронов m = m_e , в ядерном магнетоне m = m_p)
Гиромагнитные отношения для электрона, протона и нейтрона приведены в таблице

    В системе координат, связанной с частицей, орбитальное движение отсутствует. Значение магнитного момента определяется как диагональный матричный элемент оператора (2.21) в состоянии с максимальным значением проекции момента на ось z. Действие оператора проекции спина дает

Таким образом, для всех указанных частиц значение магнитного дипольного момента в магнетонах равно половине гиромагнитного отношения g_s. Принято указывать значения магнитных моментов нуклонов и ядер в ядерных магнетонах

Наблюдаемое значение магнитного момента ядра ( в ядерных магнетонах) пропорционально значению спина ядра, Коэффициент пропорциональности называется ядерным гиромагнитным отношением:

Одним из методов измерения величины ядерного спина и магнитного момента ядра является исследование сверхтонкого расщепления линий атома.

Полный момент системы электронная оболочка-ядро складывается из момента электронной оболочки I и спина ядра J. Поскольку величина магнитного поля, создаваемого электронами в области ядра, пропорциональна I, а магнитный момент ядра свяан с J (2.24) , потенциал взаимодействия является функцией скалярного произведения этих векторов:

Этот потенциал взаимодействия, входящий в полный гамильтониан атома, ответственен за тот экспериментальный факт, что состояния с разными значениями скалярного произведения векторов I и J имеют разные сдвиги в энергиях атомных уровней. Поскольку величина сдвига зависит от ядерного магнетона , она мала по сравнению с величиной тонкого расщепления атомных уровней, которые вызваны взаимодействием магнитного момента электронной оболочки с внешним магнитным полем. Поэтому расщепление атомных уровней, возникающее благодаря взаимодействию магнитного момента ядра с магнитным полем атома, называется сверхтонким. Число состояний сверхтонкого расщепления равно числу разных значений скалярного произведения векторов. Определим эту величину через квадраты квантовых векторов F, J, I:

Квадраты векторов F, J, I являются собственными операторами волновой функции атома, представляющей собой произведение волновых функций ядра и электронной оболочки ψ_a = ψ_N·ψ_e

Таким образом, число уровней сверхтонкого расщепления равно числу разных значений вектора F, который может принимать следующие значения 

Число разных значений вектора F равно 2К + 1, где К - наименьший из векторов J, I. Поскольку для калия число уровней сверхтонкого расщепления 4, эта величина не соответствует случаю, когда момент электронной оболочки 5/2 меньше спина ядра (тогда число уровней было бы равно 6). Поэтому число уровней сверхтонкого расщепления равно 4 = 2J + 1 и спин ядра J = 3/2.