Векторный и аксиально-векторный слабые токи в
унитарной симметрии и кварковой модели
4.1 Общие сведения о слабом
взаимодействии
Рассмотрим теперь применение модели
унитарной симметрии и кварковой модели к
описанию процессов слабого взаимодействия
элементарных частиц.
Несколько слов о слабом
взаимодействии. Как известно, мюоны,нейтроны, 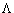 -гипероны распадаются
по слабому взаимодействию. Мы здесь упомянули
мюон, поскольку лептоны (на сегодняшний день) -
точечные, т.е. бесструктурные частицы, и
константы связи их с квантами различных полей
выступают так сказать в чистом виде, их не
затемняет структура частицы, как это происходит
у адронов. Распад мюона на электрон и два
нейтрино характеризуется константой Ферми GF ~ 10-5mp-2.
Распад нейтрона на протон, электрон и
антинейтрино характеризуется практически той же
константой связи. В то же время слабый распад -гипероны распадаются
по слабому взаимодействию. Мы здесь упомянули
мюон, поскольку лептоны (на сегодняшний день) -
точечные, т.е. бесструктурные частицы, и
константы связи их с квантами различных полей
выступают так сказать в чистом виде, их не
затемняет структура частицы, как это происходит
у адронов. Распад мюона на электрон и два
нейтрино характеризуется константой Ферми GF ~ 10-5mp-2.
Распад нейтрона на протон, электрон и
антинейтрино характеризуется практически той же
константой связи. В то же время слабый распад 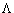 -гиперона на протон,
электрон и антинейтрино характеризуется
значительно меньшей константой связи. То же
различие характерно для констант распадов
нестранного пиона и странного каона на лептоны.
Значит ли это, что слабые взаимодействия, в
отличие от электромагнитного, неуниверсальны?
Может быть и так. А можно спасти универсальность?
Оказывается, можно, и это было сделано
Кабиббо в 1964 году
введением угла Кабиббо -гиперона на протон,
электрон и антинейтрино характеризуется
значительно меньшей константой связи. То же
различие характерно для констант распадов
нестранного пиона и странного каона на лептоны.
Значит ли это, что слабые взаимодействия, в
отличие от электромагнитного, неуниверсальны?
Может быть и так. А можно спасти универсальность?
Оказывается, можно, и это было сделано
Кабиббо в 1964 году
введением угла Кабиббо  C.
Достаточно предположить, что слабые
взаимодействия без нарушения странности
задаются не константой Ферми GF, а
константой GFcos C.
Достаточно предположить, что слабые
взаимодействия без нарушения странности
задаются не константой Ферми GF, а
константой GFcos  C,
а слабые взаимодействия с нарушением странности
задаются константой GFsin C,
а слабые взаимодействия с нарушением странности
задаются константой GFsin  C. Эта гипотеза
блестяще подтвердилась при анализе
многочисленных слабых распадов мезонов и
барионов и с сохранением, и с нарушением
странности. Значение угла Кабиббо ~ 13o. C. Эта гипотеза
блестяще подтвердилась при анализе
многочисленных слабых распадов мезонов и
барионов и с сохранением, и с нарушением
странности. Значение угла Кабиббо ~ 13o.
А как описать слабые взаимодействия
элементарных частиц?
Мы знаем, что электромагнитное
взаимодействие можно задать лагранжианом
взаимодействия вида ток x поле
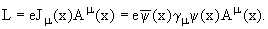
|
(4.1) |
При этом, скажем, рассеяние электрона или мюона
на электроне происходит не менее, чем во втором
порядке по е. Эффективно можно записать
рассеяние в виде ток x ток
где q2 - квадрат переданного импульса.
Оказалось, что рассматриваемые слабые распады
описываются также эффективным лагранжианом вида
ток × ток, но это
для них 1-й порядок по фермиевской константе
связи:
LW = 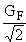 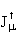  + Hermitian Conjugation.
+ Hermitian Conjugation. |
(4.3) |
При этом ток должен иметь вид
По внутренним квантовым числам ток,
описывающий 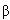 -распад
нейтрона, аналогичен -распад
нейтрона, аналогичен  --мезону,
а ток, описывающий β-распад
Λ-гиперона,
аналогичен K--мезону. Обратим внимание на
то, что слабые токи заряжены. С 1956 года
установлено, что слабые токи не сохраняют
четность. Это - одно из фундаментальных свойств
слабого взаимодействия. Структура Oμ для заряженных слабых
токов установлена из анализа многочисленных
угловых распределений и оказалась линейной
комбинацией вектора и аксиального вектора, Oμ=
γμ(1 + γ5),
что часто именуется (V-A)-вариантом теории Ферми.
При этом константы связи у адронов при --мезону,
а ток, описывающий β-распад
Λ-гиперона,
аналогичен K--мезону. Обратим внимание на
то, что слабые токи заряжены. С 1956 года
установлено, что слабые токи не сохраняют
четность. Это - одно из фундаментальных свойств
слабого взаимодействия. Структура Oμ для заряженных слабых
токов установлена из анализа многочисленных
угловых распределений и оказалась линейной
комбинацией вектора и аксиального вектора, Oμ=
γμ(1 + γ5),
что часто именуется (V-A)-вариантом теории Ферми.
При этом константы связи у адронов при  5, вообще
говоря, перенормируются (получают
дополнительный множитель, который хорошо бы
уметь рассчитывать теоретически). 5, вообще
говоря, перенормируются (получают
дополнительный множитель, который хорошо бы
уметь рассчитывать теоретически).
Размерная константа Ферми, как
показывает сравнение с электромагнитным
процессом во втором порядке по е, может быть
отражением существования очень тяжелого
W-бозона, который излучается лептонами и адронами
подобно фотону. Тогда наблюдаемые процессы
распада мюона, протона, гиперонов - процессы 2-го
порядка по константе связи gW, а GF~gW2/(q2 + MW2),
причем величиной q2 можно уверенно
пренебречь.
И тогда элементарный акт
взаимодействия со слабым полем можно записать не
через произведение ток × ток, а
просто моделируя электромагнитное
взаимодействие:
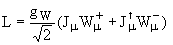 . .
|