|
| a + b → c + X. | (5.1) |
Чтобы не загромождать формулы, под 4-импульсом (или компонентами его, то есть
энергией и 3-импульсом) регистрируемой частицы будем понимать (Ec,pc), опуская
индекс c . В случае обращения к системе центра масс реакции, как всегда,
соответствующие неинвариантные величины будем помечать символом *.
Кинематическую область возможных значений импульса регистрируемой частицы
можно легко определить, пользуясь формулами для "круга импульсов" (если речь идет о системе центра масс) или
"эллипса
импульсов" (если речь идет о любой другой системе отсчета, например,
лабораторной), рассмотренными ранее. В частности, продольный импульс
регистрируемой частицы может лежать в пределах
|
|
(5.2) |
где
|
|
(5.3) |
здесь mX,min − минимальное допустимое значение эффективной массы системы X,
равное сумме масс входящих в нее частиц (имеется в виду, допустимое законами
сохранения квантовых чисел для рассматриваемой реакции). Если графически
представить круг импульсов, то
![]() принадлежит хорде круга, проведенной
перпендикулярно его вертикальному диаметру на расстоянии
принадлежит хорде круга, проведенной
перпендикулярно его вертикальному диаметру на расстоянии
![]() от горизонтального
диаметра, а границы изменения
от горизонтального
диаметра, а границы изменения
![]() определяются крайними точками этой хорды. В
лабораторной системе, где круг импульсов превращается в эллипс импульсов,
величина
определяются крайними точками этой хорды. В
лабораторной системе, где круг импульсов превращается в эллипс импульсов,
величина
![]() принадлежит хорде эллипса, проведенной перпендикулярно его малой
полуоси на расстоянии
принадлежит хорде эллипса, проведенной перпендикулярно его малой
полуоси на расстоянии
![]() от большой оси, а границы изменения
от большой оси, а границы изменения
![]() определяются
крайними точками этой хорды (см. рис. 5.1, эллипс импульсов для реакции p(p,π)X).
Т. о. экстремальные (максимальное и минимальное) возможные значения
определяются
крайними точками этой хорды (см. рис. 5.1, эллипс импульсов для реакции p(p,π)X).
Т. о. экстремальные (максимальное и минимальное) возможные значения
![]() для
реакции (5.1) определяются крайними точками большой оси этого эллипса (см.
пример на рис. 5.1, точки A, B и C для соответствующих процессов).
для
реакции (5.1) определяются крайними точками большой оси этого эллипса (см.
пример на рис. 5.1, точки A, B и C для соответствующих процессов).
Вспомнив о партонной картине взаимодействия адронов, можно заподозрить, что
инвариантная безразмерная переменная
|
xF =
|
(5.4) |
может быть хорошей переменной для анализа данных инклюзивных измерений реакций типа (5.1). Опыт показал, что так оно и есть. Переменная (5.4) называется фейнмановской скейлинговой переменной.
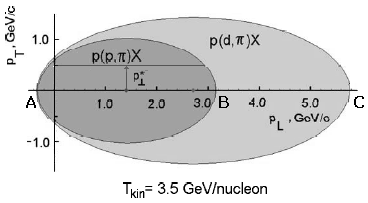
Рис. 5.1. Эллипс импульсов пиона в лабораторной системе для реакций p(p,π)X и p(d, π)X, обсужденный в Части II. Область внутри меньшего эллипса разрешена для пиона, рожденного в реакции p(p, π)X (оба нуклона - свободные). Граница большего эллипса соответствует реакции p(d,π)X, когда дейтрон рассматривается как "материальная точка", а эффективная масса системы X минимально возможная (после учета всех законов сохранения и правил отбора по квантовым числам). Область импульсов вне большего эллипса − абсолютно запрещена для пиона вследствие законов сохранения энергии и импульса. Между внешним и внутренним эллипсами − "кумулятивная" область, недоступная для реакции p(p,π)X вследствие тех же законов сохранения энергии и импульса.
Ясно, что при анализе дифференциальных распределений, проинтегрированных по
поперечному импульсу, под
![]() max следует понимать экстремальное значение
продольного импульса (например, соответствующее точке В на рис. 5.1). Кроме того,
в партонной картине Фейнмана считается, что поперечный импульс партонов невелик,
то есть их импульсное распределение в адроне "прижато" к оси абсцисс рис. 5.1,
что дает некоторое дополнительное оправдание такому рецепту определения
max следует понимать экстремальное значение
продольного импульса (например, соответствующее точке В на рис. 5.1). Кроме того,
в партонной картине Фейнмана считается, что поперечный импульс партонов невелик,
то есть их импульсное распределение в адроне "прижато" к оси абсцисс рис. 5.1,
что дает некоторое дополнительное оправдание такому рецепту определения
![]() max.
max.
В литературе часто употребляют и другое определение хF, а именно:
|
= 2 |
(5.5) |
практически совпадающее с (5.4), когда s намного больше значений всех масс,
входящих в определение (5.2), равно как и значений поперечного импульса
![]() . Определение (5.4) представляется более точным при конечных энергиях или при
работе вблизи кинематических границ рассматриваемого процесса (но все же при невысоких
. Определение (5.4) представляется более точным при конечных энергиях или при
работе вблизи кинематических границ рассматриваемого процесса (но все же при невысоких
![]() , если для
максимального значения продольного импульса принимается его экстремальная
величина).
, если для
максимального значения продольного импульса принимается его экстремальная
величина).
5.2 Быстрота и псевдобыстрота
Можно убедиться, что определенная в Части I безразмерная переменная, называемая быстротой, может быть выражена через энергии и импульсы регистрируемой частицы так:
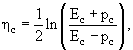 |
(5.6) |
а продольная быстрота как
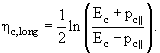 |
(5.7) |
Переменные, соответствующие динамике на световом фронте, в импульсном пространстве можно выразить через через импульсы и энергии в с.ц.м.:
|
|
(5.8) |
откуда видно, что
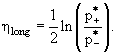 |
(5.9) |
Таким образом, существенными кинематическими переменными для анализа реакций
типа (5.1), являются пары (![]() ,xF) или (
,xF) или (![]() ,ηlong). Однако значения пределов
изменения одной из переменных в указанных парах зависят от значений другой
переменной. Это интуитивно ясно из рассмотрения рис. 5.1; подробнее это
обсуждено в книге [4]. Там же детально рассмотрена еще одна, часто употребляемая
при высоких энергиях переменная, а именно − псевдобыстрота. Ее практическая
ценность в том, что измерять псевдобыстроту проще, чем быстроту: не нужно
измерять величины импульсов, равно как и нет особой необходимости
идентифицировать частицы, чтобы правильно вычислять их энергии. Дело в том, что
для измерения псевдобыстроты достаточно измерить угол θ вылета частицы. При этом
псевдобыстрота почти везде достаточно близка к продольной быстроте.
,ηlong). Однако значения пределов
изменения одной из переменных в указанных парах зависят от значений другой
переменной. Это интуитивно ясно из рассмотрения рис. 5.1; подробнее это
обсуждено в книге [4]. Там же детально рассмотрена еще одна, часто употребляемая
при высоких энергиях переменная, а именно − псевдобыстрота. Ее практическая
ценность в том, что измерять псевдобыстроту проще, чем быстроту: не нужно
измерять величины импульсов, равно как и нет особой необходимости
идентифицировать частицы, чтобы правильно вычислять их энергии. Дело в том, что
для измерения псевдобыстроты достаточно измерить угол θ вылета частицы. При этом
псевдобыстрота почти везде достаточно близка к продольной быстроте.
Вначале заметим, что
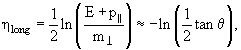
|
|
(5.10) |
(величина
![]() называется
"поперечной массой"), если выполнены условия:
называется
"поперечной массой"), если выполнены условия:
- угол вылета много меньше 1 но не слишком мал:
| m/p < θ <<1; | (5.11) |
- поперечный импульс много меньше продольного:
|
|
(5.12) |
- импульсы велики по сравнению с массами:
|
p ≥
|
(5.13) |
Если несколько ослабить первое условие, то есть допустить, что
| m/p < θ <1, | (5.14) |
то можно увидеть, что
|
|
(5.15) |
Последнее приближенное равенств в этой формуле используется как определение псевдобыстроты, позволяющее ограничиться измерениями углов вылета частиц в лабораторной системе:
|
|
(5.16) |
Следует заметить, что в разных работах по изучению процессов множественного
рождения частиц в инклюзивной постановке экспериментов при высоких энергиях
нередко используются слегка разные определения псевдобыстроты (см. например
[4]). Поэтому небесполезно внимательно следить за тем, какое именно определение
псевдобыстроты используется в той или иной работе, хотя все такие определения
отталкиваются от углов вылета регистрируемой частицы.
Безусловно, необходимо помнить о различии между псевдобыстротой и настоящей
быстротой.
Наконец, нельзя не сказать и о том, что (уступая давлению жаргона) продольную
быстроту иногда также называют просто быстротой (см. примеры в [4]).
Рисунок 5.1 помогает понять, почему переменная псевдобыстроты в свое время
стала популярной. Действительно, партонная картина неупругого взаимодействия
подразумевает, что при высоких энергиях средние поперечные импульсы вторичных
частиц почти не растут с ростом начальной энергии (или растут достаточно
медленно). Иными словами, область внутри разрешенного кинематикой эллипса
"заселяется" частицами неравномерно: они концентрируются вблизи оси абсцисс в
довольно узкой полосе. С ростом энергии эллипс расширяется, но частицы остаются
почти в той же полосе: распределение по поперечному импульсу при фиксированной
быстроте почти не меняется, и когда поперечный импульс частицы много меньше ее
полного импульса, распределение по продольному импульсу становится (приближенно)
распределением по углу вылета частицы. Это означает, что характер распределения
событий внутри эллипса не зависит (или слабо зависит) от его абсолютных размеров:
важно лишь относительное расстояние точки, изображающей событие, от центра
эллипса (круга в с.ц.м.).
5.3 Связь быстроты и переменной хF.
В определениях (5.4) фейнмановской переменной и продольной быстроты (5.7) фигурирует один и тот же продольный импульс регистрируемой частицы с. Отсюда следует, что эти переменные связаны между собой. Эту связь нетрудно установить:
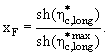 |
(5.17) |
Можно убедиться, что вблизи | xF | ~ 0 продольная быстрота тоже мала: |![]() | ~ 0, но в этой, т. н.
"центральной" области, данный конечный фиксированный
интервал ∆xF с ростом энергии столкновения (√s) отображается на растущий с √s интервал быстроты (см. например, [4]). Иными словами, быстрота
"растягивает" центральную область по сравнению с | xF |.
| ~ 0, но в этой, т. н.
"центральной" области, данный конечный фиксированный
интервал ∆xF с ростом энергии столкновения (√s) отображается на растущий с √s интервал быстроты (см. например, [4]). Иными словами, быстрота
"растягивает" центральную область по сравнению с | xF |.
Вблизи кинематических границ можно переписать связь xF с быстротой в другой
форме. В самом деле, рассмотрим выражения для них в системе центра масс вблизи
границы xF ≈ 1 и
![]() ≈
≈
![]() .
.
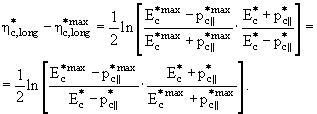 |
(5.18) |
Поскольку сами эти переменные обычно применяются в области высоких энергий и,
как правило, при анализе неупругих процессов с довольно высокой
множественностью, можно считать
![]() >> mc. Это вполне оправдано вблизи
кинематических пределов. Приняв это приближение, из (5.18) имеем
>> mc. Это вполне оправдано вблизи
кинематических пределов. Приняв это приближение, из (5.18) имеем
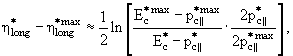 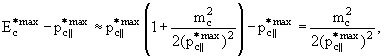 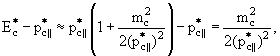 |
(5.19) |
поскольку вблизи границы | xF | ≈ 1 перпендикулярный импульс
![]() много меньше
продольного
много меньше
продольного
![]() .
.
В результате, приходим к формуле
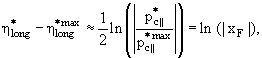 |
(5.20) |
которую удобнее выписать в окончательной форме [4]
|
xF ≈ exp ( xF ≈ exp (| |
(5.21) |