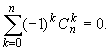(x + a)n = xn + |
(2.27) |
(x + a)n = xn + |
(2.27) |
называется формулой бинома Ньютона.
Применив символ 
для обозначения суммы и вспомнив, что 
=
=
1, формулу (2.27) можно записать в виде
|
(2.28) |
Для доказательства (2.28)
рассмотрим произведение n биномов
(x + a1)(x + a2)...(x + an). |
(2.29) |
Открыв скобки, получим
(x + a1)(x + a2)...(x + an)
= xn + (a1 + a2 +... + an)xn-1 + |
(2.30) |
Коэффициент при xn-1 является суммой
всевозможных сочетаний из элементов a1a2...an
по одному элементу, поэтому число слагаемых
равно 
. Коэффициент у xn-2
является суммой произведений элементов
всевозможных сочетаний из тех же элементов a1a2...an
по два элемента, а следовательно, число слагаемых
равно 
. Вообще,
коэффициент xk, является суммой
произведений элементов всевозможных сочетаний
из элементов a1a2...an
по k элементов, и поэтому число таких
слагаемых равно 
.
Если a1 = a2 =... = an = a,
то из формулы (2.30) следует, что
(x + a)n = xn + axn-1 + a2xn-2 + ... +
an-1xn + an,
т. е. формула (2.27) доказана. 
Замечание. Положив в формуле (2.28) x = a = 1, получим
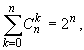
а положив x = 1, a = -1, получим
