4.6*. Счетность рациональных чисел. Несчетность
действительных чисел
Сравнение множеств осуществляется с
помощью понятия взаимно однозначного
соответствия.
Определение 5. Два множества,
между элементами которых можно установить
взаимно однозначное соответствие (биекцию),
называются равномощными.
Замечание. Нетрудно убедиться, что
если множество X равномощно множеству Y,
а множество Y равномощно Z, то и
множество X равномощно множеству Z.
Множество X называется конечным,
если существует такое натуральное число n
(называемое числом элементов множества X),
что между элементами множества X и
элементами множества {1, 2, ..., n -1, n}
можно установить взаимно однозначное
соответствие.
Очевидно, два конечных
множества равномощны тогда и только тогда, когда
они содержат одинаковое число элементов.
Пустое множество по определению считается
конечным. Множества, не являющиеся конечными,
называются бесконечными.
Приведем примеры равномощных
бесконечных множеств.
Примеры.
1. Множество четных натуральных чисел
равномощно множеству всех натуральных чисел.
Действительно, соответствие n 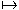 2n, 1, 2, ..., является
биекцией множества натуральных чисел N и множества всех четных
натуральных чисел.
2n, 1, 2, ..., является
биекцией множества натуральных чисел N и множества всех четных
натуральных чисел.
2. Множество всех целых чисел
равномощно множеству натуральных чисел. В самом
деле, соответствие
2n 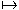 n,
n = 1, 2, ...,
n,
n = 1, 2, ...,
2n + 1 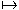 -n,
n = 0, 1, 2, ...,
-n,
n = 0, 1, 2, ...,
является биекцией множества натуральных чисел N и множества целых чисел Z.
3. Любые два конечных интервала
(соответственно отрезка) числовой прямой
равномощны. Если заданы два интервала (a,b)
и (c,d), то отображение
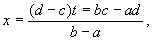 a
< t < b,
a
< t < b,
является биекцией интервалов (a,b) и (c,d)
(соответственно отрезков [a,b] и [c,d]).
4. Множество всех действительных чисел R равномощно любому конечному
интервалу числовой оси. В силу замечания после
определения 5 и примера 3 достаточно
показать, что множество действительных чисел
равномощно хотя бы одному интервалу, поэтому
достаточно заметить, что функция 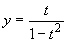 устанавливает взаимно
однозначное соответствие между точками
интервала (-1,1) и точками всей числовой оси.
устанавливает взаимно
однозначное соответствие между точками
интервала (-1,1) и точками всей числовой оси.
Примеры 1, 2 и 4 показывают, что в
случае бесконечных множеств собственное
подмножество бесконечного множества может
оказаться равномощным всему множеству.
5. Пусть задано некоторое
множество X. Всякое отображение множества
натуральных чисел N в
множество X, т. е. отображение вида f: N 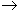 X,
называется последовательностью элементов
множества X. Элемент f(n), n
X,
называется последовательностью элементов
множества X. Элемент f(n), n  N,
обозначается через xn и называется n-м
членом последовательности f: N
N,
обозначается через xn и называется n-м
членом последовательности f: N 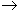 X,
число n - его номером, и сам элемент f(n)
X,
число n - его номером, и сам элемент f(n)
 X - значением
этого члена.
X - значением
этого члена.
Последовательность f: N 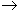 X
обозначается также {xn} или xn,
n = 1, 2, ...
X
обозначается также {xn} или xn,
n = 1, 2, ...
Отметим, что член
последовательности задается его значением и
номером. Если n > m, то член
последовательности xn называется
членом, следующим за членом xm.
Множество членов последовательности равномощно
с множеством натуральных чисел, так как каждому
натуральному числу соответствует член
последовательности и разным натуральным числам
соответствуют разные члены последовательности,
отличающиеся друг от друга по крайней мере
номерами. Таким образом, множество членов
последовательности всегда бесконечно, в то время
как множество значений членов
последовательности, т. е. множество значений
функции f: N 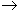 X (иначе говоря,
подмножество множества X, на которое
посредством отображения f отображается
множество N
натуральных чисел), может оказаться конечным
множеством, в частности состоять из одного
элемента. В последнем случае, т. е. тогда, когда
у последовательности все значения ее элементов
совпадают, она называется стационарной.
X (иначе говоря,
подмножество множества X, на которое
посредством отображения f отображается
множество N
натуральных чисел), может оказаться конечным
множеством, в частности состоять из одного
элемента. В последнем случае, т. е. тогда, когда
у последовательности все значения ее элементов
совпадают, она называется стационарной.
Определение 6. Множество,
равномощное множеству натуральных чисел,
называется счетным.
Из рассмотренных выше примеров 1, 2 и 5
следует, что множества всех четных чисел, всех
целых чисел и всех членов любой
последовательности являются счетными.
Пусть X - счетное множество,
т. е. существует взаимно однозначное
отображение (биекция) множества натуральных
чисел N на
множество X. Элемент множества X,
соответствующий при этом отображении числу n,
обозначим, как и в случае последовательности, xn
и будем называть число n его номером. Поэтому
можно сказать, что множество является счетным,
если его элементы можно перенумеровать
натуральными числами. Отличие определения
счетного множества от последовательности
состоит в том, что в случае последовательности
рассматриваемое отображение множества
натуральных чисел не обязано быть биекцией: не
исключается случай, когда разным натуральным
числам окажется поставленным в соответствие
один и тот же элемент. Отсюда следует, что
множество значений членов последовательности
либо конечно, либо счетно, т. е., как говорят, не
более чем счетно.
Лемма1. Любое бесконечное множество
содержит бесконечное счетное подмножество.
 Пусть X -
бесконечное множество; тогда оно во всяком
случае непусто, т. е. в нем существует по
крайней мере один элемент, обозначим его через x1.
Поскольку множество X бесконечно, то
множество X \ {x1} также
непусто, т. е. содержит по крайней мере один
элемент, обозначим его x2. Продолжая
этот процесс, на n-м шаге получим элемент xn.
Поскольку X - бесконечное множество, то
множество X \ {x1, x2, ..., xn}
непусто, т. е. содержит по крайней мере один
элемент, обозначим его xn+1 и т. д.
Множество {x1, x2, ..., xn,
...} - искомое счетное подмножество множества X.
Пусть X -
бесконечное множество; тогда оно во всяком
случае непусто, т. е. в нем существует по
крайней мере один элемент, обозначим его через x1.
Поскольку множество X бесконечно, то
множество X \ {x1} также
непусто, т. е. содержит по крайней мере один
элемент, обозначим его x2. Продолжая
этот процесс, на n-м шаге получим элемент xn.
Поскольку X - бесконечное множество, то
множество X \ {x1, x2, ..., xn}
непусто, т. е. содержит по крайней мере один
элемент, обозначим его xn+1 и т. д.
Множество {x1, x2, ..., xn,
...} - искомое счетное подмножество множества X. 
Лемма 2. Любое бесконечное
подмножество счетного множества счетно.
 Пусть X -
счетное множество: X = {x1, x2, ..., xn,
...} и Y
Пусть X -
счетное множество: X = {x1, x2, ..., xn,
...} и Y 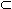 X.
Обозначим через y1 элемент из Y,
имеющий наименьший номер в X, через y2 -
элемент множества Y, имеющий следующий
ближайший номер, и т. д. Поскольку каждый
элемент множества Y является некоторым
элементом xn множества X и,
следовательно, имеет номер n, то через
конечное число шагов (не больше, чем n) он
получает некоторый номер m и в множестве Y,
т. е. будет обозначен ym, причем,
поскольку множество Y бесконечно, этот
процесс может быть продолжен неограниченно.
Таким образом, все элементы множества Y
окажутся перенумерованными, что и означает
счетность этого множества.
X.
Обозначим через y1 элемент из Y,
имеющий наименьший номер в X, через y2 -
элемент множества Y, имеющий следующий
ближайший номер, и т. д. Поскольку каждый
элемент множества Y является некоторым
элементом xn множества X и,
следовательно, имеет номер n, то через
конечное число шагов (не больше, чем n) он
получает некоторый номер m и в множестве Y,
т. е. будет обозначен ym, причем,
поскольку множество Y бесконечно, этот
процесс может быть продолжен неограниченно.
Таким образом, все элементы множества Y
окажутся перенумерованными, что и означает
счетность этого множества. 
Теорема. Множество всех
рациональных чисел счетно.
 Расположим все
рациональные числа в таблицу, содержащую
бесконечное число строк и столбцов, следующим
образом (см. таблицу):
Расположим все
рациональные числа в таблицу, содержащую
бесконечное число строк и столбцов, следующим
образом (см. таблицу):

Здесь в n-ю строчку помещены
рациональные числа, записываемые несократимыми
рациональными дробями со знаменателем n и
упорядоченные по возрастанию их абсолютных
величин, причем непосредственно за каждым
положительным числом следует ему
противоположное. Очевидно, что каждое
рациональное число находится на каком-то месте в
этой таблице.
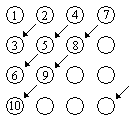
Занумеруем теперь элементы
получившейся таблицы согласно следующей схеме, в
которой в кружочках стоят номера
соответствующих элементов, а стрелки указывают
направление нумерации. В результате все
рациональные числа оказываются занумерованными,
т. е. множество Q
рациональных чисел счетно. 
Возникает естественный вопрос,
существуют ли несчетные множества, т. е.
бесконечные множества, не являющиеся счетными, a
если существуют, то интересно построить пример
несчетного множества.
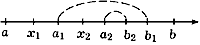
Рис. 48
|
Лемма 3. Любой отрезок множества
действительных чисел состоит из несчетного
множества точек.
 Допустим противное: пусть
точки некоторого отрезка [a,b], a
Допустим противное: пусть
точки некоторого отрезка [a,b], a  R,
b
R,
b  R, a < b, можно
занумеровать: [a,b] = {x1,x2...,xn,...}.
Выберем акой-либо отрезок [a1,b1]
лежащий на [a,b] и не содержащий точки x1
(рис. 48):
R, a < b, можно
занумеровать: [a,b] = {x1,x2...,xn,...}.
Выберем акой-либо отрезок [a1,b1]
лежащий на [a,b] и не содержащий точки x1
(рис. 48):
x1 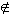 [a1,b1]
[a1,b1] 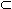 [a,b].
[a,b].
Далее выберем отрезок [a2,b2],
лежащий на [a1,b1] и не
содержащий точки x2, и т. д. Таким
образом, если выбран отрезок [an,bn],
то выберем отрезок [an+1,bn+1],
лежащий на [an,bn] и не
содержащий точки xn+1. Продолжая этот
процесс, получим систему вложенных отрезков [an,bn],
n = 1, 2, ..., такую, что
xn 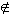 [an,bn], n
= 1, 2, ... [an,bn], n
= 1, 2, ... |
(4.28) |
Следовательно, ни одна точка xn
не принадлежит пересечению 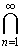 [an,bn], но согласно
принципу вложенных отрезков (см. п. 4.5, теорема 3) существует
точка, обозначим ее
[an,bn], но согласно
принципу вложенных отрезков (см. п. 4.5, теорема 3) существует
точка, обозначим ее 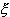 , принадлежащая всем отрезкам [an,bn]:
, принадлежащая всем отрезкам [an,bn]:
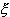  [an,bn],
n = 1, 2, ..., [an,bn],
n = 1, 2, ..., |
(4.29) |
а поэтому и отрезку [a,b], ибо [an,bn]
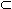 [a,b] при всех
n = 1, 2, ... А так как все точки отрезка
[a,b] по предположению перенумерованы, то
точка
[a,b] при всех
n = 1, 2, ... А так как все точки отрезка
[a,b] по предположению перенумерованы, то
точка 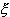 также
должна иметь какой-то номер, т. е. существует
такое натуральное число n0, что
также
должна иметь какой-то номер, т. е. существует
такое натуральное число n0, что 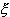 =
=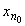 , и тогда согласно (4.29)
получим
, и тогда согласно (4.29)
получим
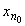  [an,bn],
n = 1, 2, ... [an,bn],
n = 1, 2, ... |
(4.29) |
В частности, 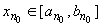 , а это
противоречит условию (4.28).
, а это
противоречит условию (4.28). 
Теорема 6 (Кантор).
Множество всех действительных чисел несчетно.
 Если бы множество всех
действительных чисел было счетным, то было бы
счетным, согласно лемме 2, и любое его
подмножество, в частности, любой отрезок, что
противоречит лемме 3.
Если бы множество всех
действительных чисел было счетным, то было бы
счетным, согласно лемме 2, и любое его
подмножество, в частности, любой отрезок, что
противоречит лемме 3. 
Принцип вложенных отрезков
Оглавление Определение
предела числовой последовательности