4.5. Принцип вложенных отрезков

    Определение 3. Система числовых отрезков

называется системой вложенных отрезков, если

т. е. если (рис. 47)

[a₁,b₁] [a₂,b₂] ... [a_n,b_n] ...

    Теорема 3. Всякая система вложенных числовых отрезков имеет непустое пересечение.
Пусть задана система вложенных отрезков (4.22). Обозначим через A множество всех левых концов a_n отрезков этой системы, а через B - множество их правых концов b_n. Из неравенств (4.23) следует, что для любых номеров m и n выполняется неравенство a_m < b_n. Поэтому по свойству непрерывности действительных чисел (п. 2.1, свойство V) существует такое число , что для всех номеров m и n выполняется неравенство

a_m <  < b_n,

в частности, неравенство a_n <  < b_n, n = 1, 2, ... Это и означает, что точка принадлежит всем отрезкам [a_n,b_n]. 
    Укажем условие, при котором пересечение системы вложенных отрезков состоит из единственной точки.

    Определение 4. Длины b_n - a_n отрезков [a_n,b_n], a_n R, b_n R, a_n < b_n, n = 1, 2, ..., называются стремящимися к нулю, если для любого числа > 0 существует такой номер , что для всех номеров n > выполняется неравенство

    Теорема 4. Для всякой системы вложенных отрезков [a_n,b_n], n = 1, 2, ..., длины которых стремятся к нулю, существует единственная точка , принадлежащая всем отрезкам данной системы; при этом

Если точки и принадлежат всем отрезкам рассматриваемой системы, т. е.

  [a_n,b_n], [a_n,b_n],    n = 1, 2, ...,.

то ясно, что для всех номеров n выполняются неравенства

| - | < b_n - a_n,

а следовательно, в силу условия (4.24) для любого > 0 справедливо неравенство

    Поскольку > 0 - произвольное число, то это возможно только тогда, когда = (если бы , то, например, при = | - | неравенство (4.26) было бы противоречиво). Это означает, что существует единственное число , принадлежащее всем отрезкам [a_n,b_n]:

a_n <  < b_n,   n = 1, 2, ...

Из этих неравенств видно, что число ограничивает сверху числа a_n и снизу числа b_n, поэтому если
= sup { a_n}, = inf {b_n}, то в силу определения верхней и нижней граней будут выполняться неравенства

Таким образом, числа , и принадлежат всем отрезкам [a_n,b_n], а следовательно, по доказанному выше они равны, т. е. выполняется условие (4.25). 
    Замечание 1. Для интервалов и полуинтервалов множества действительных чисел аналог принципа вложенных отрезков не имеет места. Например,

.

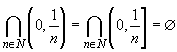Замечание 2. Для множества одних только рациональных чисел принцип вложенных отрезков несправедлив. При этом под отрезком в множестве рациональных чисел понимается пересечение обычного отрезка, концы которого являются рациональными числами, с множеством рациональных чисел:

[a,b] Q  = {x Q: a < x < b}, a Q,   b Q,

Например, пусть числа a_n и b_n представляют собой десятичные приближения числа с недостатком и с избытком и имеют по n десятичных знаков после запятой,   n = 1, 2, ...,  тогда

 [a,b] Q   =

так как  [a,b] = {} и  - иррациональное число: Q.

Принцип Архимеда  Оглавление Счетность рациональных чисел