Пусть aj
Рассмотрим одно преобразование
конечных сумм вида ![]() ajbj
, принадлежащее Абелю
и часто весьма полезное при исследовании
сходимости рядов.
ajbj
, принадлежащее Абелю
и часто весьма полезное при исследовании
сходимости рядов.
Пусть aj ![]() C, bj
C, bj
![]() C,
Bj = b1 + ... + bj, j = 1,
2, ..., n и, следовательно, B1 = b1,
bj = Bj - Bj-1,
j = 2, 3, ..., n. Тогда
C,
Bj = b1 + ... + bj, j = 1,
2, ..., n и, следовательно, B1 = b1,
bj = Bj - Bj-1,
j = 2, 3, ..., n. Тогда
a1b1 + a2b2
+ ... + anbn = a1B1
+ a2(B2 - B1)+ ... + an(Bn
- Bn-1) =
= (a1 - a2)B1 + (a2
- a3)B2 + ... +(an-1 - an)Bn-1
+ anBn,
или, используя знак суммирования,
|
(30.72) |
Это равенство называется преобразованием
Абеля суммы ![]() ajbj
. Если его переписать в виде
ajbj
. Если его переписать в виде
![]() aj(Bj - Bj-1)
= anBn - a1B1 -
aj(Bj - Bj-1)
= anBn - a1B1 - ![]() (aj+1
- aj)Bj,
(aj+1
- aj)Bj,
то видно, что его можно рассматривать как
дискретный аналог интегрирования по частям.
В дальнейшем числа aj будут
действительными, а bj, вообще говоря,
комплексными.
Лемма 3 (Абель). Если для всех
j = 1, 2, ..., n - 1 выполняются
неравенства
aj < aj+1 или aj > aj+1, |
(30.73) |
и для всех j = 1, 2, ..., n - неравенства
|b1 + b2 + ... + bj| < B, |
(30.74) |
то
|
(30.75) |
![]() Имеем
Имеем
![]()
![]() ajbj
ajbj![]()
![]()
![]() |aj - aj+1||Bj|
+ |an||Bn|
|aj - aj+1||Bj|
+ |an||Bn| ![]() B
B![]()
![]() |aj
- aj+1| + |an|
|aj
- aj+1| + |an|![]()
![]() B
B![]()
![]()
![]() aj
- aj+1
aj
- aj+1![]() + |an|
+ |an|![]() =
=
= B(|a1 - an| + |an|)
< B(|a1| + 2|an|).
Мы воспользовались здесь очевидным равенством
![]() |aj - aj+1|
= |(a1 - a2) + (a2
- a3) + ... +(an-1 - an)| = |a1
- an|.
|aj - aj+1|
= |(a1 - a2) + (a2
- a3) + ... +(an-1 - an)| = |a1
- an|. ![]()
Теорема 16 (признак Дирихле). Если последовательность {an} монотонная и
|
(30.76) |
а последовательность частичных сумм ряда ![]() bn ограничена,
то ряд
bn ограничена,
то ряд
|
(30.77) |
сходится.
![]() Из
ограниченности последовательности частичных
сумм Bn =
Из
ограниченности последовательности частичных
сумм Bn = ![]() bk, n = 1, 2, ..., ряда
bk, n = 1, 2, ..., ряда ![]() bn следует, что
существует такое число B > 0, что для
всех n = 1, 2, ... выполняются неравенства |Bn| < B
и, следовательно, для всех n = 2, 3, ... и
всех p = 0, 1, ... - неравенства
bn следует, что
существует такое число B > 0, что для
всех n = 1, 2, ... выполняются неравенства |Bn| < B
и, следовательно, для всех n = 2, 3, ... и
всех p = 0, 1, ... - неравенства
|
(30.78) |
Зафиксируем произвольно ![]() > 0. В силу
условия (30.76) существует такой номер n0,
что для всех n > n0
имеет место неравенство
> 0. В силу
условия (30.76) существует такой номер n0,
что для всех n > n0
имеет место неравенство
|an| < |
(30.79) |
Поэтому для всех n > n0 и всех p = 0, 1, 2, ... будем иметь
![]()
![]() an+kbn+k
an+kbn+k![]()
![]() 2B(|an| + 2|an+p|)
2B(|an| + 2|an+p|)
![]() 2B(
2B(![]() + 2
+ 2![]() ) =
) = ![]() ,
,
т. е. ряд (30.77) удовлетворяет критерию Коши
сходимости рядов и, следовательно, сходится. ![]()
Теорема 17 (признак Абеля). Если последовательность {an} ограничена и монотонна, а ряд
|
(30.80) |
сходится, то сходится и ряд
|
(30.81) |
![]() Из
ограниченности и монотонности
последовательности {an} следует
существование конечного предела
Из
ограниченности и монотонности
последовательности {an} следует
существование конечного предела ![]() an = a, и потому
последовательность {an - a}
монотонная и стремится к нулю. Из сходимости же
ряда (30.80) следует, что последовательность {Bn}
его частичных сумм Bn =
an = a, и потому
последовательность {an - a}
монотонная и стремится к нулю. Из сходимости же
ряда (30.80) следует, что последовательность {Bn}
его частичных сумм Bn = ![]() bk ограниченная.
Теперь имеем
bk ограниченная.
Теперь имеем
![]() anbn
=
anbn
= ![]() [(an - a)
+ a]bn =
[(an - a)
+ a]bn = ![]() (an -
a)bn + a
(an -
a)bn + a![]() bn.
bn.
Второй ряд в правой части равенства
сходится по условию теоремы, а первый - в силу
признака Дирихле. Поэтому сходится и ряд, стоящий
в левой части равенства, т. е. ряд (30.81). ![]()
Примеры.
1. Ряд
|
(30.82) |
сходится. Действительно, последовательность an = 1/n, n = 1, 2, ..., монотонно убывая, стремится к нулю, а
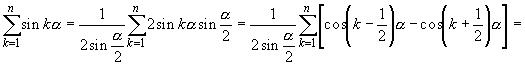
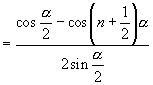 ,
, ![]()
![]() 2m
2m![]() , m = 0, +1, ...
, m = 0, +1, ...
Поэтому
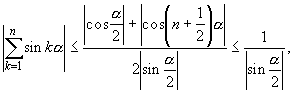
т. е. при ![]()
![]() 2m
2m![]() , m = 0,
+1, ... , все рассматриваемые суммы ограничены.
Отсюда в силу признака Дирихле следует, что при
, m = 0,
+1, ... , все рассматриваемые суммы ограничены.
Отсюда в силу признака Дирихле следует, что при ![]()
![]() 2m
2m![]() , m = 0, +1, ...,
ряд (30.82) сходится. Он сходится, очевидно, и при
, m = 0, +1, ...,
ряд (30.82) сходится. Он сходится, очевидно, и при ![]() = 2m
= 2m![]() , m = 0,
+1, ..., так как в этом случае все члены его
обращаются в нуль.
, m = 0,
+1, ..., так как в этом случае все члены его
обращаются в нуль.
Итак, ряд (30.82) сходится при всех ![]()
![]() R.
R.
2. Ряд
|
(30.83) |
сходится по признаку Абеля, ибо сходится
ряд (30.82), а последовательность {cos ![]() /n} ограниченна и монотонна.
/n} ограниченна и монотонна.
Условно сходящиеся ряды Оглавление Исследование сходимости рядов методом выделения главной части ряда