32.5. Формула Стирлинга

    Разложение функции ln (1 + x) в степенной ряд дает возможность легко получить асимптотическую формулу для факториала n! при n. Эта формула называется  формулой Стирлинга; она имеет вид

т. е. отношение n! к выражению, стоящему в правой части этой формулы, стремится к 1 при n.
    Действительно, если |x| < 1, то

ln = ln (1 + x) - ln (1 - x) =  (-1)ⁿ⁺¹xⁿ/n - (xⁿ/n) = 2xx²ⁿ/(2k + 1).

    Положив x = 1/(2n + 1), n = 1, 2, ... получим

ln (1 + 1/n) = =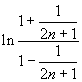
= 1 + + + ... > = ,

откуда

(n + 1/2)ln (n + 1/2) > 1.

Пропотенцировав и заметив, что функция ln x возрастает, а 1 = ln e, получим

Положим

Поскольку, согласно неравенству (32.77),

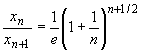>1,

то последовательность {x_n} убывает. Кроме того, она ограничена снизу: x_n > 0. Следовательно, она имеет конечный предел. Обозначим его a:

Покажем, что a0. Так как

 + + ... <  + + ... = = ,

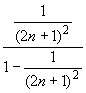то

(n + 1/2)ln (n + 1/2) < 1 +

и, следовательно,

(1 + 1/n)^n+1/2 < e^{1+1/(12n(n+1))}.

Поэтому

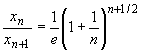< e^{1+1/(12n(n+1))} = .

т. е.

Последовательность y_n = x_ne^-1/(12n), n = 1, 2, ..., будучи произведением двух последовательностей {x_n} и {e^-1/(12n)}, имеющих предел, также имеет предел, причем

y_n = x_ne^-1/(12n)  a.

    Неравенство (32.80) означает, что последовательность {y_n} возрастает, поэтому y_n, а так как y_n > 0, то доказано, что a > 0.
    Из равенства (32.79) следует, что

где _n = 0. Подставив (32.81) в (32.78), получим

    Для того чтобы найти значение числа a, вспомним, что по формуле Валлиса (см. (26.9) в п. 26.2)

    Из формулы (32.82) следует, что

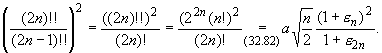
Подставив это выражение в формулу Валлиса (32.83), получим

откуда a = . Следовательно,

n! = (1 + _n),     

т. е. формула Стирлинга (32.76) доказана. 

Разложение элементарных функций в ряд Тейлора  Оглавление