1.Разложение в ряд функции f(x)
= ex. Поскольку f (n)(x)
= ex, то для любого фиксированного a > 0,
для всех x ![]() (-a,a)
и всех n = 1, 2, ... выполняется неравенство
(-a,a)
и всех n = 1, 2, ... выполняется неравенство
0 < f (n)(x) < ea.
Таким образом, на интервале (-a,a) для функции ex выполнены условия теоремы 7 (x0 = 0) и, следовательно, функция ex раскладывается в ряд Тейлора на любом конечном интервале, а потому и на всей числовой оси. Заметив, что в данном случае f (n)(0) = 1, получим (см. (32.47))
ex= |
(32.50) |
Напомним, что в п. 31.1
было установлено, что ряд ![]() zn/n!
абсолютно сходится на всей комплексной
плоскости (впрочем, это независимо от
предыдущего следует согласно первой теореме
Абеля и из доказанной здесь сходимости
ряда (32.50) на всей действительной числовой оси).
В силу формулы (32.50) для действительных z = x
его сумма равна ex. В случае существенно
комплексных z его сумму по аналогии
обозначают ez. Таким образом, формула
zn/n!
абсолютно сходится на всей комплексной
плоскости (впрочем, это независимо от
предыдущего следует согласно первой теореме
Абеля и из доказанной здесь сходимости
ряда (32.50) на всей действительной числовой оси).
В силу формулы (32.50) для действительных z = x
его сумма равна ex. В случае существенно
комплексных z его сумму по аналогии
обозначают ez. Таким образом, формула
ez= |
(32.51) |
для существенно комплексных чисел z
является определением функции ez.
Так определенная функция ez, z
![]() C,
не только совпадает для действительных z = x
с известной показательной функцией ex,
но и сохраняет в комплексной области ряд свойств
показательной функции действительного
аргумента. Например,
C,
не только совпадает для действительных z = x
с известной показательной функцией ex,
но и сохраняет в комплексной области ряд свойств
показательной функции действительного
аргумента. Например,
|
(32.52) |
Действительно, ряды, полученные из (32.51) при z = z1 и z = z2, абсолютно сходятся, поэтому их можно почленно перемножить; так как получившийся при этом ряд также абсолютно сходится, то его члены можно располагать в произвольном порядке. Соберем все члены, содержащие произведения степеней z1 и z2 с одинаковой суммой показателей, равной n, расположим эти группы по возрастанию n, а затем умножим и разделим их на 1/n!:
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]() =
=
= ![]()
![]()
![]()
![]() =
=![]()
![]() =
= ![]() .
.
2. Разложение в ряды sh x и ch x. Заменив в формуле (32.50) x на -x (это означает просто изменение обозначения), получим
e-x = |
(32.53) |
Сложив и вычтя равенства (32.50) и (32.53), а затем деля их на 2, получим
ch x = (ex + e-x)/2
= |
(32.54) |
sh x = (ex - e-x)/2
= |
(32.55) |
В правых частях этих формул в силу
единственности разложений функций в степенные
ряды стоят ряды Тейлора соответственно функций
ch x и sh x.
Поскольку функция ez
определена для всех комплексных значений
аргумента z, то на существенно комплексные
значения аргумента можно распространить и
гиперболические функции ch x и sh x, положив
ch z ![]() (ez + e-z)/2,
sh z
(ez + e-z)/2,
sh z ![]() (ez
- e-z)/2, z
(ez
- e-z)/2, z ![]() C.
C.
Определенные таким образом функции
ch z и sh z для комплексных z раскладываются
в степенные ряды (32.54) и (32.55) (в которых
вместо x надо написать z), сходящиеся на
всей комплексной плоскости.
3. Разложение в ряды sin x и cos x.
Формула Эйлера.
Если f (n)(x) =
sin x, то f (n)(x) = sin (x +
n![]() /2), n = 1, 2, ... (см. п. 11.1), поэтому | f (n)(x)| < 1
для всех действительных x. Согласно
теореме 7 отсюда следует, что функция sin x
раскладывается в степенной ряд на всей
действительной числовой оси. Вспомнив формулу
Тейлора для синуса (см. п. 14.2), получим для него
ряд Тейлора
/2), n = 1, 2, ... (см. п. 11.1), поэтому | f (n)(x)| < 1
для всех действительных x. Согласно
теореме 7 отсюда следует, что функция sin x
раскладывается в степенной ряд на всей
действительной числовой оси. Вспомнив формулу
Тейлора для синуса (см. п. 14.2), получим для него
ряд Тейлора
sin x = |
(32.56) |
Рассуждая аналогично для cos x и вспоминая его формулу Тейлора, получим
cos x = |
(32.57) |
В силу первой теоремы Абеля ряды, стоящие в правых частях формул (32.56) и (32.57), сходятся на всей комплексной плоскости. Это позволяет распространить синус и косинус на комплексные значения аргумента, положив для любого комплексного z
sin z = |
(32.58) |
cos z = |
(32.59) |
В комплексной области легко установить связь между показательной и тригонометрическими функциями. Заменив z в ряде (32.51) сначала на iz, а затем на -iz, получим
eiz = |
(32.60) |
Заметив, что i2k = (-1)k и, следовательно, i2k+1 = (-1)ki, k = 0, 1, 2, ..., из (32.60) получим
(eiz + e-iz)/2 =![]() (-1)k
(-1)k![]() , (eiz - e-iz)/2i
=
, (eiz - e-iz)/2i
=![]() (-1)k
(-1)k![]() ,
,
Сравнив эти формулы с (32.58) и (32.59), видим, что
cos z = (eiz + e-iz)/2,
sin z = (eiz - e-iz)/2i,
z |
(32.61) |
В силу определения ch z и sh z для комплексных значений переменной z (см. выше) формулы (32.61) можно записать в виде
ch iz = cos z, sh iz = isin z.
Таким образом, в комплексной области cos z
может быть получен из функции ch z с
помощью замены переменной z = i![]() , а функция sin z - из
sh z той же заменой и делением на i:
, а функция sin z - из
sh z той же заменой и делением на i:
ch z = ch i![]() = cos
= cos![]() , sh z = sh i
, sh z = sh i![]() = isin
= isin![]() .
.
Из формул (32.61) непосредственно следует также формула
cos z + isin z = eiz. |
(32.62) |
Формулы (32.61) и (32.62) называются формулами
Эйлера. Они, конечно, справедливы и для
действительных значений z.
Если в формуле (32.62) z = ![]() - действительное
число, то
- действительное
число, то
cos |
(32.63) |
Отсюда следует, что модуль комплексного числа
вида ![]() ,
, ![]()
![]() R, равен 1:
R, равен 1:
![]() = (cos2
= (cos2 ![]() + isin2
+ isin2 ![]() )1/2 = 1.
)1/2 = 1.
Из формулы (32.63) следует также, что
комплексное число z с модулем r и
аргументом ![]() , т. е.
, т. е.
z = r(cos ![]() + isin
+ isin ![]() ), можно записать в виде
), можно записать в виде
z = ![]() .
.
Положив здесь r = 1, ![]() =
= ![]() и, следовательно, z = -1,
получим
и, следовательно, z = -1,
получим
![]() = -1
= -1
- удивительную формулу, открытую Эйлером,
устанавливающую связь между числами -1, ![]() , i и e. Удивительную
потому, что эти числа были открыты математиками
при изучении весьма далеких друг от друга задач:
число -1 появилось тогда, когда было понято, что
при введении отрицательных чисел операция
вычитания приобретает смысл для любой
упорядоченной пары натуральных чисел (кроме
того, отрицательные числа оказались удобными при
сравнении температур тел с температурой
замерзания воды, при измерении высот и низин на
земле относительно уровня моря и т. п.); число
, i и e. Удивительную
потому, что эти числа были открыты математиками
при изучении весьма далеких друг от друга задач:
число -1 появилось тогда, когда было понято, что
при введении отрицательных чисел операция
вычитания приобретает смысл для любой
упорядоченной пары натуральных чисел (кроме
того, отрицательные числа оказались удобными при
сравнении температур тел с температурой
замерзания воды, при измерении высот и низин на
земле относительно уровня моря и т. п.); число ![]() является отношением длины
окружности к диаметру, мнимая единица i дает
возможность решать любое квадратное уравнение с
действительными коэффициентами, а число e
представляет собой такое основание
показательной функции, при котором с ней
совпадает ее производная. Поэтому не
удивительно, что в городе Кингстоне в Канаде на
фасаде главного здания Королевского
университета можно увидеть огромную формулу
Эйлера:
является отношением длины
окружности к диаметру, мнимая единица i дает
возможность решать любое квадратное уравнение с
действительными коэффициентами, а число e
представляет собой такое основание
показательной функции, при котором с ней
совпадает ее производная. Поэтому не
удивительно, что в городе Кингстоне в Канаде на
фасаде главного здания Королевского
университета можно увидеть огромную формулу
Эйлера: ![]() = -1.
= -1.
Из формулы (32.63) следует неожиданное, на
первый взгляд, свойство функции ez -
она оказывается периодической на комплексной
плоскости и ее период равен 2![]() i.
Действительно, так как
i.
Действительно, так как
![]()
![]() cos 2
cos 2![]() + isin 2
+ isin 2![]() = 1.
= 1.
то для любого z имеем
![]() = ez
= ez![]()
![]() = ez.
= ez.
Отсюда следует, что обратная к функции ez функция, обозначаемая ln z и определяемая равенством
eln z = z,
является в комплексной области многозначной функцией. Имея для комплексного переменного понятие экспоненциальной функции ez и логарифмической функции ln z, можно для любых комплексных чисел z и w определить степень
wz
по формуле
wz = ezln w.
Упражнение. Доказать, что все
значения ii являются действительными
числами.
Из того, что функция ez имеет
период 2![]() i, вытекает, что
функции cos z и sin z остаются
периодическими с периодом 2
i, вытекает, что
функции cos z и sin z остаются
периодическими с периодом 2![]() и
для комплексных значений аргумента:
и
для комплексных значений аргумента:
cos (z + 2![]() )
)![]() (
(![]() +
+ ![]() )/2 = (eiz + e-iz)/2 =
cos z, z
)/2 = (eiz + e-iz)/2 =
cos z, z ![]() C.
C.
Аналогично sin (z + 2![]() ) =
sin z, z
) =
sin z, z ![]() C.
C.
Замечание. Понятие функции
комплексной переменной бывает полезно
использовать и при изучении функций
действительного аргумента, принимающих только
действительные значения. Покажем это на примере
вычисления интеграла ![]() .
Применив формулу Эйлера
.
Применив формулу Эйлера
![]() ,
,
получим
![]() =
= ![]()
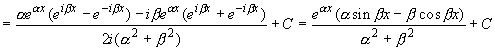
(ср. с вычислением этого интеграла в п. 22.4).
4. Разложение в ряд ln(1 + x).
Согласно формуле Тейлора
ln(1 + x) = x - x2/2 + x3/3 - ... +(-1)n+1xn/n + rn(x), x > -1.
Запишем остаточный член rn(x) этой формулы в виде Лагранжа. Так как
(ln (1 + x))(n+1) = (-1)nn!/(1+x)(n+1),
то
rn(x) = 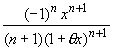 , 0 <
, 0 < ![]() <1
<1
(![]() , как всегда, зависит от x
и от n).
, как всегда, зависит от x
и от n).
Если 0 < x < 1,
то 0 < 1/(1 + ![]() x) <
1. Поэтому |rn(x)| < 1/(n + 1}
и, следовательно,
x) <
1. Поэтому |rn(x)| < 1/(n + 1}
и, следовательно,
|
(32.64) |
Если же -1 < x < 0, то запишем остаточный член rn(x) в виде Коши:
rn(x) = 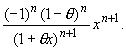
Здесь x = -|x| и поэтому
0 < ![]() =
= ![]() <1,
<1,
ибо в числителе дроби ![]() из 1 вычитается большее число, чем в знаменателе:
из 1 вычитается большее число, чем в знаменателе: ![]() |x| <
|x| < ![]() . Кроме того,
. Кроме того,
![]()
ибо ![]() |x| < |x|.
Поэтому при x
|x| < |x|.
Поэтому при x ![]() (-1,0) имеем
(-1,0) имеем
|rn(x)| = 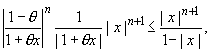
и так как |x| < 1, то и здесь
|
(32.65) |
Из (32.64) и (32.65) следует, что для всех x ![]() (-1,1] справедливо
разложение
(-1,1] справедливо
разложение
ln (1 + x) = |
(32.66) |
При x = -1 этот ряд расходится, так как его члены только знаком минус отличаются от членов гармонического ряда, который, как мы знаем, расходится. Расходится ряд, стоящий в правой части формулы (32.66), и при всех x, больших по абсолютной величине единицы, так как в этом случае последовательность его членов не стремится к нулю; более того,
![]() (-1)n+1xn/n
=
(-1)n+1xn/n
= ![]() ,
|x| >1.
,
|x| >1.
Если воспользоваться второй теоремой Абеля (п. 32.1), отмеченной звездочкой, как необязательной при сокращенной программе, то разложение функции ln (1 + x) в степенной ряд можно получить косвенным, но более коротким путем. Рассмотрим следующий ряд, представляющий собой сумму членов бесконечно убывающей геометрической прогрессии:
1/(1 + x) = 1 - x + x2 - x3 + ... + (-1)nxn + ..., |x| < 1. |
(32.67) |
Ряд в правой части равенства
сходится равномерно на любом отрезке [-q,q],
0 < q < 1. Это следует, например, из признака
Вейерштрасса, ибо при |x| < q
выполняются, очевидно, неравенства |(-1)nxn| < qn,
n = 0, 1, 2, ...$, а числовой ряд ![]() qn сходится.
qn сходится.
Из равномерной сходимости ряда (32.67)
вытекает, что его можно почленно интегрировать
от 0 до x ![]() (-1,1) (теорема 8 из п. 31.4). Выполнив
это интегрирование, получим
(-1,1) (теорема 8 из п. 31.4). Выполнив
это интегрирование, получим
ln (1 + x) = x - x2/2 + x3/3 - x4/4 +... + (-1)nxn+1/(n + 1) + ...,
или, записав правую часть с помощью знака суммирования,
ln (1 + x) = ![]() (-1)n+1xn/n.
(-1)n+1xn/n.
При этом, согласно указанной теореме, ряд в
правой части этого равенства сходится на
интервале (-1,1), а по признаку Лейбница
(теорема 9 из п. 30.5) он сходится и в точке x = 1.
Следовательно, согласно второй теореме Абеля (теорема 3* из п. 32.1), сумма
ряда ln (1 + x) = ![]() (-1)n+1xn/n
непрерывна на отрезке [0,1]. Но так как функция
ln (1 + x) также непрерывна на этом
отрезке, а на интервале (-1,1) совпадает с суммой
рассматриваемого ряда, то, устремив x к 1,
получим, что функция ln (1 + x) и сумма
ряда
(-1)n+1xn/n
непрерывна на отрезке [0,1]. Но так как функция
ln (1 + x) также непрерывна на этом
отрезке, а на интервале (-1,1) совпадает с суммой
рассматриваемого ряда, то, устремив x к 1,
получим, что функция ln (1 + x) и сумма
ряда ![]() (-1)n+1xn/n
совпадают и при x = 1. Таким образом, мы
снова пришли к разложению функции ln (1 + x)
в степенной ряд на промежутке (-1,1] (см. (32.66)).
(-1)n+1xn/n
совпадают и при x = 1. Таким образом, мы
снова пришли к разложению функции ln (1 + x)
в степенной ряд на промежутке (-1,1] (см. (32.66)).
5. Разложение в степенной ряд степени
бинома ![]() . Формула
Тейлора для функции
. Формула
Тейлора для функции ![]() имеет вид
имеет вид
|
(32.68) |
Соответствующий ряд, называемый биномиальным рядом с показателем , имеет имеет вид
1 + |
(32.69) |
Если ![]() является
натуральным числом, то этот ряд содержит лишь
конечное число членов, не равных 0, и превращается
в известную формулу бинома Ньютона
является
натуральным числом, то этот ряд содержит лишь
конечное число членов, не равных 0, и превращается
в известную формулу бинома Ньютона
![]() =
= ![]()
![]() xn.
xn.
Будем предполагать, что ![]() не является натуральным числом и что x
не является натуральным числом и что x![]() 0, тогда все члены ряда
(32.69) не равны 0. Исследуем его абсолютную
сходимость с помощью признака Даламбера. Положив
0, тогда все члены ряда
(32.69) не равны 0. Исследуем его абсолютную
сходимость с помощью признака Даламбера. Положив
un = |![]() (
(![]() - 1)...(
- 1)...(![]() - n
+ 1)xn/n!|.
- n
+ 1)xn/n!|.
получим
![]() un+1/un
=
un+1/un
= ![]() |
|![]() - n||x|/(n
+ 1) = |x|.
- n||x|/(n
+ 1) = |x|.
Следовательно, ряд (32.69) абсолютно сходится при |x| < 1
и, поскольку этот ряд степенной, расходится при |x| > 1.
Докажем, что суммой ряда (32.69) на интервале (-1,1)
является функция ![]() . Для
этого исследуем остаточный член rn(x)
в формуле Тейлора (32.68), записав его в виде Коши.
Поскольку
. Для
этого исследуем остаточный член rn(x)
в формуле Тейлора (32.68), записав его в виде Коши.
Поскольку
[![]() ](n + 1)
=
](n + 1)
= ![]() (
(![]() -
1)...(
-
1)...(![]() - n)
- n)![]() ,
,
то
rn(x) = ![]() (
(![]() - 1)...(
- 1)...(![]() - n)
- n)![]() (1 -
(1 - ![]() )nxn+1/n!,
0 <
)nxn+1/n!,
0 < ![]() <1.
<1.
Положим
an(x) = (![]() - 1)[(
- 1)[(![]() - 1) - 1]...[(
- 1) - 1]...[(![]() - 1) - n + 1])xn/n!,
- 1) - n + 1])xn/n!,
bn(x) = ![]() x
x![]() ; cn(x)
= [(1 -
; cn(x)
= [(1 - ![]() )/(1 +
)/(1 + ![]() x)]n;
x)]n;
тогда
rn(x) = an(x)bn(x)cn(x), n = 1, 2, ... |
(32.70) |
Сомножитель an(x) является членом
биномиального ряда с показателем ![]() - 1, и так как выше было показано, что любой
биномиальный ряд сходится на интервале (-1,1), то
- 1, и так как выше было показано, что любой
биномиальный ряд сходится на интервале (-1,1), то
|
(32.71) |
Далее, из неравенств
1 - |x| < 1 - ![]() |x| < 1+
|x| < 1+![]() x < 1 +
x < 1 + ![]() |x| < 1 + |x|,
|x| < 1 + |x|,
где -1 < x <1, следует, что значения bn(x)
заключены между числами |![]() x|(1
-
x|(1
- ![]() и |
и |![]() x|(1 +
x|(1 + ![]() , не
зависящими от n, т. е. последовательность {bn(x)}
ограничена при каждом x
, не
зависящими от n, т. е. последовательность {bn(x)}
ограничена при каждом x ![]() (-1,1).
(-1,1).
Что же касается последовательности {cn(x)},
то она ограничена равномерно на всем интервале
(-1,1):
cn(x) = [(1 - ![]() )/(1 +
)/(1 + ![]() x)]n <
[(1 -
x)]n <
[(1 - ![]() )/(1 -
)/(1 - ![]() |x|)]n < 1.
|x|)]n < 1.
а это означает, что на интервале (-1,1) имеет место разложение
|
(32.72) |
Сходимость ряда, стоящего в правой части
равенства, в точках x = -1 и x = 1
требует дополнительного исследования. Можно
показать, что в точке x = 1 при ![]() > -1 биномиальный ряд
сходится, а при
> -1 биномиальный ряд
сходится, а при ![]() < -1
расходится. В точке x = -1 при
< -1
расходится. В точке x = -1 при ![]() > 0 он абсолютно
сходится, а при
> 0 он абсолютно
сходится, а при ![]() < 0
расходится. При этом, согласно второй теореме
Абеля, всякий раз, когда биномиальный ряд (32.69)
сходится, его сумма равна
< 0
расходится. При этом, согласно второй теореме
Абеля, всякий раз, когда биномиальный ряд (32.69)
сходится, его сумма равна ![]() .
.
Иногда для получения разложения
функции в степенной ряд вместо оценки
остаточного члена в формуле Тейлора проще
воспользоваться каким-либо уже известным
разложением и из него с помощью общих теорем о
функциональных рядах получить искомое
разложение. Поясним сказанное на нижеследующем
примере.
6. Разложение arctg x. Найдем
производную arctg x и разложим ее в
степенной ряд по формуле для суммы бесконечно
убывающей геометрической прогрессии:
(arctg x)' = 1/(1 + x2)
= |
(32.73) |
Ряд, стоящий в правой части равенства, имеет радиус сходимости R = 1, и поэтому его можно почленно интегрировать на интервале (-1,1)
arctg x = |
(32.74) |
Радиус сходимости получившегося
ряда также равен 1 (см. теорему 3). Таким
образом, функция arctg x оказалась
разложенной в степенной ряд с радиусом
сходимости, равным единице. На первый взгляд это
представляется несколько неожиданным, так как
arctg x является бесконечно
дифференцируемой на всей числовой оси функцией.
Это связано с тем, что производная функции arctg x
заведомо не может быть разложена в степенной
ряд с радиусом сходимости больше единицы, так как
функция 1/(1 + x2) обращается в
бесконечность при z = + i.
Важно отметить, что разложение (32.74)
справедливо и на концах x = +1
интервала сходимости (-1, 1). Действительно, при x = +1
ряд, стоящий в правой части равенства (32.74),
сходится в силу признака Лейбница, а тогда его
сумма $s(x)$, согласно следствию из второй теоремы
Абеля (теорема 3* в
п. 32.1), непрерывна на отрезке [-1,1]. Таким
образом, две непрерывные на отрезке [-1, 1] функции
arctg x и s(x) совпадают в силу
равенства (32.74) на интервале (-1, 1), а тогда они
совпадают при x = +1, т. е. и при
этих значениях x функция arctg x является
суммой ряда, стоящего в правой части
равенства (32.74):
arctg x = |
(32.75) |
При подстановке в разложение функции
в ряд какого-либо фиксированного значения
переменной получается формула для суммы
соответствующего числового ряда. Так, подставив
в ряд (32.75) x = 1 и заметив, что arctg 1 = ![]() /4, получим
/4, получим
![]() /4 =
/4 =![]() (-1)n/(2n + 1).
(-1)n/(2n + 1).
7. Разложение arcsin x. Заметив, что
(arcsin x)' = (1 - x2)-1/2,
разложим (arcsin x)' в ряд по формуле разложения степени бинома (см. 32.72)
(arcsin x)' = (1 - x2)-1/2
= 1 + ![]()
![]() x2n.
x2n.
Радиус сходимости получившегося ряда, как для всякого биномиального ряда, равен единице. Интегрируя получившийся ряд от нуля до x, |x| < 1, получим
arcsin x =![]()
![]() = x +
= x + ![]()
![]()
Разложение функций в степенные ряды. Различные способы записи остаточного члена формулы Тейлора Оглавление Формула Стирлинга