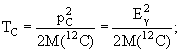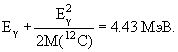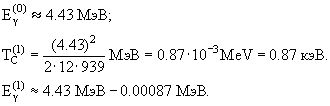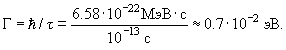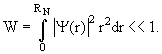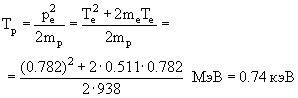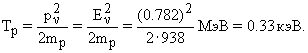Тема 3. Законы сохранения1. Законы сохранения в распадах и реакциях Структура и
свойства частиц и атомных ядер исследуются уже около ста лет в
распадах и реакциях.
Реакция − превращение двух взаимодействующих между собой частиц или ядер в два или более продуктов реакции:
Как распады, так и реакции подчиняются ряду законов сохранения, среди которых должны быть упомянуты, во-первых, следующие законы:
В дальнейшем будут обсуждаться
и другие законы сохранения, действующие в распадах и реакциях.
Перечисленные выше законы являются важнейшими и, что особенно
существенно, выполняются во всех типах взаимодействий (возможно,
что закон сохранения барионного заряда не обладает такой
универсальностью, как законы сохранения 1 − 4, однако пока не
обнаружено его нарушения).
2. Распады Спонтанный
распад любого объекта физики микромира (ядра или частицы) возможен в
том случае, если масса покоя продуктов распада меньше массы первичной
частицы. Примеры спонтанных распадов:
В распадах (левая
колонка) в конечном состоянии – две частицы. В распадах (правая
колонка) – три.
Интегрирование (3.5) с учетом начальных условий дает для связи числа частиц в момент времени t с числом этих же частиц в начальный момент времени t = 0:
Периодом полураспада называется время, за которое число частиц (или ядер) уменьшится вдвое:
В таблицах частиц обычно указывают среднее время жизни τ, в таблицах ядер – периоды полураспада Т1/2. 3. Кинематика распадов
Разность масс
первичной частицы и продуктов распада распределяется среди продуктов
распада в виде их кинетических энергий. MX = MA + TA + MB
+ TB; Сумма кинетических энергий продуктов определяется разностью масс TA + TB = Q = MX − MA − MB, а отношение кинетических энергий TA/TB = MB/MA. Отсюда получаем для кинетических энергий продуктов распада
Таким образом, в случае двух
частиц в конечном состоянии кинетические энергии продуктовопределены однозначно. Это утверждение не зависит от того, релятивистские или
нерелятивистские скорости имеют продукты распада. Для релятивистского
случая формулы для кинетических энергий выглядят несколько сложнее,
чем (3.8), но решение уравнений для энергии и импульса двух частиц
опять-таки является единственным. Если в конечном состоянии возникает
три (или более) продуктов, решение уравнений для законов сохранения
энергии и импульса не приводит к однозначному результату. Это
означает, что только в случае распада
на две частицы спектры продуктов распада − дискретные. Применим полученные формулы (3.8) к α-распаду радия – 226Ra. Тогда величина Q = M(226Ra) − M(222Rn) − M(4He) = Δ(226Ra) − Δ(222Rn) − Δ(4He) = 4.87 МэВ.
По определению (3.9) Δ(12С) = 0. Кинетические энергии ядер радона и гелия (α-частицы), возникших в результате α-распада, равны
Суммарная
кинетическая энергия, выделившаяся в результате α-распада,
меньше 5 МэВ и составляет около 0.5% от массы покоя нуклона. Соотношение
выделившейся в результате распада кинетической энергии и энергий
покоя частиц или ядер − критерий
допустимости применения нерелятивистского приближения.
В случае α-распадов
ядер малость кинетических энергий по сравнению с энергиями покоя
позволяет ограничиться нерелятивистским приближением.
Q = Δ(222Rn) – Δ(218Po) – Δ(4He)
5.59 МэВ Возникающее
в этом распаде ядро 218Po также распадается с излучением α-частиц
(период его полураспада Т1/2 = 3.1 мин): 218Po →
214Pb + 4He.
Продукт этого распада 214Pb
"перегружен" нейтронами (стабильными являются изотопы
свинца 206Pb, 207Pb, 208Pb).
Поэтому ядро 214Pb
распадается (Т1/2 = 27 минут) по каналу β-распада.
Период полураспада 238U на несколько порядков величины больше, чем периоды полураспадов всех остальных членов радиоактивного семейства. Для всех членов семейства, например i-го, (за исключением первого − 238U и последнего − стабильного изотопа 206Pb), изменение числа ядер связано с ростом числа ядер за счет распада предыдущего члена "цепочки", т.е. (i-1)-го элемента, и распадом ядер данного i-го элемента:
За время, прошедшее после образования элементов, установилось т.н. "вековое" равновесие, когда прибыль и убыль ядер данного нестабильного элемента в цепи распадов компенсируют друг друга. При этом активности (т.е. числа распадов в 1 секунду) всех членов радиоактивного семейства выравниваются:
Суммарная активность
радиоактивного препарата, т.е. число распадов в секунду, которое этот
препарат испытывает, определяется не только числом распадов в единицу
времени первичного ядра, но и активностями всех получаемых в
результате распадов продуктов. Часто эти продукты распадов вносят в
суммарную активность значительно больший вклад, чем первичный распад.
Наиболее вероятный (99.98%) распад π+-мезона происходит на две частицы: π+ → μ+ + νμ. Масса π+-мезона равна 139.6 МэВ, масса мюона μ равна 105.7 МэВ. Точное значение массы мюонного нейтрино νμ неизвестно, но установлено, что она меньше 10 кэВ. Из наблюдения нейтринных осцилляций следует, что все типы нейтрино имеют ненулевую массу покоя. Так как разность масс π+-мезона и продуктов его распада равна 33.8 МэВ, для нейтрино необходимо использовать релятивистские формулы связи энергии и импульса. В дальнейшем расчете малой массой покоя нейтрино можно пренебречь и считать нейтрино ультрарелятивистской частицей. Законы сохранения энергии и импульса в распаде π+-мезона: mπ = mμ + Tμ + Eν,
0 =
Кинетическая энергия мюонного нейтрино π+-распада равна Eν ≈ Tν = (mπ − mμ) − Tμ = 29.7 МэВ.
Законы сохранения системе покоя возбужденного ядра имеют вид: M(12С*) = M(12С) + TC
+ Eγ; pC = pγ = Eγ.
Поскольку второй член (энергия отдачи) в последнем уравнении на несколько порядков меньше первого, вместо решения квадратного уравнения удобно применить метод последовательных приближений:
Поправка к энергии γ-кванта равна энергии отдачи ядра и она меньше третьей значащей цифры
в полученном результате для энергии испущенного ядром
электромагнитного кванта. Однако
этот сдвиг в энергии вылетевшего γ-кванта
относительно энергии уровня ядра оказывается препятствием для
резонансного поглощении ядерных γ-квантов
невозбужденными ядрами. Оценим ширину Г
первого возбужденного состояния ядра
12С.
(это соотношение является одной из
формулировок соотношения неопределенностей для энергии и времени).
Мы получили, что ширина возбужденного уровня ядра
на несколько порядков меньше сдвига энергии уровня, возникающего
вследствие отдачи ядра (задача 3.5).
Резонансного поглощения происходить не может! 4. Трехчастичные распады
Примерами трехчастичных распадов являются β-распады.
n → p + e- +
β-распады испытывают и сами лептоны, например, мюон (среднее время жизни мюона τ = 2.2·10–6сек): μ- → e- +
В атомных
ядрах как нейтроны, так и протоны находятся в связанном состоянии.
Спонтанные превращения связанных в ядре нуклонов друг в друга
возможны и определяются соотношением масс начального ядра и продуктов
распада.
Рассмотрим закон сохранения энергии для этих
процессов. Напомним, что в таблицах для масс (или избытков масс)
приведены массы нейтральных атомов, к которым и следует привести
уравнения для законов сохранения. В дальнейших выкладках массы
нейтральных атомов не помечены индексами, а для масс ядер введен
индекс N (nucleus).
Для β+-распада получим аналогичным образом из уравнения для масс ядер уравнение для масс нейтральных атомов:
Для е-захвата:
Сравнение двух последних уравнений показывает, что для двух ядер-изобар е-захват имеет менее «жесткие» энергетические условия, чем β+-распад (в обоих случаях происходит превращение одного из протонов ядра в нейтрон). Однако поскольку е-захват представляет собой захват ядром электрона с атомной оболочки, вероятность этого процесса пропорциональная вероятности W «пребывания электрона внутри ядра», т.е.
Вероятность захвата К-электрона
во много раз выше, чем электронов с других атомных оболочек, т.к. для К-электронов
величина интеграла в (3.16) больше, чем для электронов других
оболочек.
3H → 3He + e- +
Закон сохранения импульса этого процесса
0 =
Электрон имеет максимальный импульс и максимальную энергию, если pe = pN + pν = [2M(3He)·TN]1/2 + Eν. Здесь использован тот факт,
что для кинетической энергии ядра применимо нерелятивистское
приближение, а нейтрино (точнее − антинейтрино) –
ультрарелятивистская частица. Импульс конечного ядра не превышает
суммы модулей импульсов лептонов (электрона и антинейтрино).
Поскольку масса ядра более чем на три порядка величины превышает
массу электрона, кинетическая энергия ядра примерно на три порядка
меньше суммы кинетических энергий лептонов. Te + Eν = 0.019 МэВ = 19 кэВ. Электрон
уносит максимальную кинетическую энергию, если энергия антинейтрино,
излучаемого вместе с ним, близка к 0. Максимальная энергия, которую
может унести антинейтрино этого распада, равна максимальной энергии
электрона. Антинейтрино уносит максимальную энергию в случае, когда
кинетическая энергия электрона близка к 0.
Разность масс покоя начального и конечного
состояний в распаде n -→ p + e- +
-
В случае, когда максимальную энергию уносит антинейтрино, кинетическая энергия протона
В рассмотренных примерах β-распадов разность масс покоя начального и конечного состояний практически полностью уносилась двумя лептонами. Это является следствием большой, сравнительно с лептонами, массы конечного ядра (в последнем примере – протона).
Сумма энергии нейтрино и энергии отдачи ядра лития равны Eν + TLi = (7Be) – (7Li) = (15.768 – 14.907) МэВ = 0.861 МэВ. Энергией связи электрона на атомной орбите в данном расчете можно пренебречь. Импульсы нейтрино и ядра лития равны и противоположны, поэтому
Действуя методом последовательных приближений, получим
Таким образом, спектры энергий продуктов е-захвата имеют дискретный характер. |
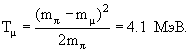
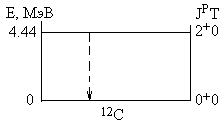 Примером двухчастичного
распада является также излучение γ-кванта при переходе
возбужденного ядра 12С* на низший
энергетический уровень: 12С* → 12Сgr.state
+ γ.
Примером двухчастичного
распада является также излучение γ-кванта при переходе
возбужденного ядра 12С* на низший
энергетический уровень: 12С* → 12Сgr.state
+ γ.