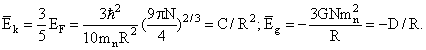Модель Ферми-газа

    В модели Ферми-газа (ФГМ) нуклоны в ядре рассматриваются как нерелятивистские фермионы, движущиеся в потенциальной яме. Главным допущением модели является предположение, что линейные размеры ямы гораздо больше нуклонных длин волн:

(6.1)

    В качестве первого приближения рассмотрим решение уравнения Шредингера для частиц в бесконечно глубокой прямоугольной потенциальной яме. В этом случае решение у. Ш. удобно искать в виде произведения трех волновых функций:

() = (x)(y)(z)

(6.2)

Решение у. Ш. внутри ямы имеет простой вид:

. (x) = a sin kxx + b cos kxx, (x) = 0 b = 0,  (L) = 0 kxL =  nx.

(6.3)

Здесь n - целое число. Последние условия являются следствием “сшивания” волновой функции внутри и извне ямы. Полная энергия частицы в яме:

(6.4)

где N- целое число - соответствует числу заполненных состояний в яме, причем из (6.1) следует, что N >> 1.

Рис. 6.1.Уровни нуклонов в яме в ФГМ.

Рис. 6.2.

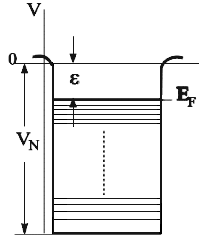
    Максимальная энергия частицы в яме называется энергией Ферми (см. рис.6.1):

.

(6.5)

Из уравнения (6.4) получим дифференциал числа состояний в яме:

dN = dnxdnydnz = L3dkxdkydkz /3 = L3K2dKd/3.

(6.6)

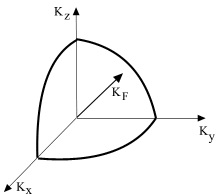
    Число состояний частицы с энергиями E < E_F равно интегралу от (6.6), причем лишь по положительным значениям волновых векторов (рис.6.2). Ограничение положительными значениями импульса уменьшит (6.6) в 8 раз. Чтобы получить число возможных состояний нуклона в потенциальной яме, нужно учесть две возможные проекции спина нуклона на ось и две проекции изоспина (т.е. протоны и нейтроны). Тогда число состояний должно равняться числу нуклонов А:

.

(6.7)

Объем ямы V равен объему ядра: V = (4/3)R³ = (4/3)r₀³A.
    Оценим нуклонную плотность ядра . Используя равенство (6.7), одновременно найдем связь импульса Ферми с экспериментально измеряемым параметром r₀:

.	(6.8)
;  .	(6.9)

    Получаем, что нуклонная плотность ядра (6.8) приблизительно постоянна.
    Нуклонная плотность ядер экспериментально определена в опытах по рассеянию электронов промежуточных энергий (Е > 100 МэВ) на ядрах. Дополнили эти эксперименты опыты по рассеянию протонов тех же энергий. Результатом этих опытов было представление о распределении плотности ядерной материи в виде распределения Ферми:

.

(6.10)

При этом получено, что

R r0A1/3,  r0 (1.2 - 1.3) Фм.

(6.11)

Нуклонная плотность ядер, согласно этим измерениям, близка к константе, для средних и тяжелых ядер почти на зависит от А и приближенно составляет ₀ 0.17 Фм^-3.
   Из (6.9) получим значение импульса Ферми:

KF (1.25 - 1.35) Фм-1(250 - 270) МэВ/c.

(6.12)

    Отсюда значение максимальной кинетической энергии частиц Ферми-газа (энергии Ферми) составляет E_F (35 - 38) МэВ. Следует подчеркнуть, что эта величина в ФГМ не зависит от числа нуклонов в ядре. Отсюда можно получить и приближенную величину глубины ядерной потенциальной ямы. Поскольку средняя энергия отделения нуклона от ядра составляет около 8 МэВ, глубина потенциальной ямы V₀ = E_F + (42 - 46) МэВ (cм. рис.6.1).
    Оценку этой же величины можно получить из других соображений, например из решения задачи о потенциале дейтрона. Таким образом, простая модель Ферми-газа приводит к разумным оценкам глубины потенциальной ядерной ямы.

Рис.6.3. Сечение неупругого рассеяния электронов на ядре 40Са.

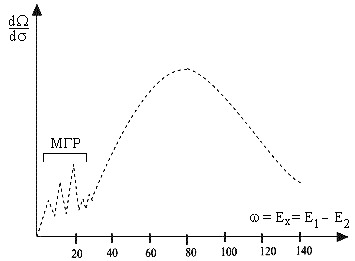
    Тот факт, что нуклоны ядра находятся в движении, особенно наглядным образом проявляется в реакциях квазиупругого рассеяния электронов. Сечение этого процесса представляет собой широкий максимум, расположенный выше по энергии, чем область возбуждения мультипольных гигантских резонансов в ядрах (см. рис.6.3). Если бы рассеяние электрона происходило на неподвижном нуклоне, максимум находился бы при переданной ядру энергии, связанной с переданным ядру импульсом q простым нерелятивистским соотношением = q²/M*, где = ₁ - ₂ - переданный импульс, M* - “эффективная” масса нуклона в ядре. Но вместо узкого пика при этой энергии на кривой сечения наблюдается широкий максимум. Его ширина обусловлена именно фермиевским движением нуклонов ядра. Рассеяние электрона происходит – в предельных случаях – как на нуклоне, движущемся навстречу электрону, так и параллельно импульсу электрона. Поэтому измерение ширин пиков квазиупругого рассеяния является способом независимого определения величины импульса Ферми. В табл.1 для нескольких ядер приведены значения импульсов Ферми, рассчитанные из данных по квазиупругому рассеянию электронов.

Таблица 6.1. Импульсы Ферми для некоторых ядер.

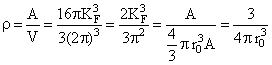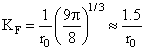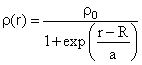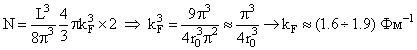Модель Ферми-газа в астрофизике

    Взрыв сверхновых звезд приводит к появлению либо нейтронных звезд, либо черных дыр. Судьба сверхновой зависит в первую очередь от массы. Фермиевская энергия электронов в звезде так велика, что во время взрыва в звезде происходит превращение протонов и электронов в пары нейтрон-нейтрино (обратный β-распад: p + e^- n + ν_e). Процесс обычного β-распада нейтронов запрещен принципом Паули для электронов (плотность вещества настолько велика, что все уровни энергии электронов заняты, включая те, которые могли бы быть заняты испускаемым в этом распаде электроном). “Выгорание” протонов приводит к исчезновению железного кора звезды и превращению ее в нейтронный Ферми-газ:

+ 25e^- 56n + 26ν_e.

    Число состояний в потенциальной яме N будет равно количеству нейтронов:

;
1 Фм^-1 = 200 МэВ (с200 МэВ·Фм = 1) k_F(320 - 380) МэВ/с;
E_F(50 - 70) МэВ.

    Гравитационному сжатию системы противостоит давление Ферми-газа. Если масса кора сверхновой больше удвоенной массы Солнца, гравитационные силы преодолевают давление Ферми-газа, и звезда превращается в черную дыру. При меньших массах идет превращение кора сверхновой в нейтронную звезду, в которой уравновешены силы гравитационного сжатия и давление нейтронного газа. Масса нейтронной звезды примерно M_nst 1.5M_Sun 3·10³⁰ кг, (рассчитано из данных по наблюдению доплеровского смещения), тогда N_n M_nst/m_n 1.8^.10⁵⁷ - число нейтронов в звезде.
    Для получения условия равновесия звезды необходимо оценить среднюю кинетическую энергию ферми-движения в звезде как функцию радиуса звезды.

.

В нейтронной звезде импульс Ферми , радиус звезды связан с числом нейтронов N:

Rr₀N^1/3; N = M_nst/m_n 1.5M_Sun/m_n = 1.8·10⁵⁷, отсюда R13 км.

    Оценку радиуса звезды можно получить также из условия равновесия, введя в него зависимости средней кинетической энергии фермиевского движения и средней гравитационной энергии сжатия от радиуса звезды:

Из условия равновесия получаем

(G = 6.7^.10^-39с.(ГэВ/c²)^-2.)