Глава 3.
Электромагнитные взаимодействия: природа и основные закономерности

    С использованием описанных выше экспериментальных методов к настоящему времени накоплен [1 – 4] огромный экспериментальный материал по фоторасщеплению атомных ядер: детально исследованы вероятности взаимодействия с ядрами фотонов различных энергий (сечения или функции возбуждения полных и парциальных реакций с вылетом различных частиц и/или их комбинаций), энергетические и угловые распределения продуктов реакций. Кроме того накоплена разнообразная информация о большом количестве других параметров электромагнитных взаимодействий – асимметрии, поляризации, и др.
    В настоящей работе рассмотрение будет посвящено, главным образом, основным параметрам гигантского дипольного резонанса (ГДР), проявляющегося, как было отмечено во Введении, не только в сечении реакции фотопоглощения, но и в сечениях всех парциальных реакций: после поглощения ядром фотона происходит распад образовавшейся в области ГДР ядерной системы с испусканием различных частиц – нейтронов, протонов, дейтронов, α-частиц и их комбинаций. Изучение каналов распада ГДР позволяет исследовать механизмы распада ядра в этой области энергий.
    Как показано в Главе 1, сечение фотопоглощения может быть измерено прямо, а может быть «собрано» из сечений отдельных парциальных каналов (соотношение (13) Главы 1). Поэтому сечения реакций для таких парциальных каналов распада ГДР также весьма важны для определения параметров ГДР.

3.1. Основные параметры гигантских дипольных резонансов

    Представление о том, как выглядит ГДР для разных ядер, дает Рис. 1. На нем приведены сечения реакции фотопоглощения (γ,abs)для ядер различного размера и формы (ядра могут быть сферическими и деформированными (Рис. 2).
    В легких сферических (Рис. 2, середина) ядрах (например, в ядре ¹²C) в сечении реакции наблюдается несколько хорошо выраженных резонансов, которые, тем не менее, не приводят к изменению формы единственного основного максимума.
    В средне-тяжелых деформированных (Рис. 2, слева и справа) ядрах (пример – ¹⁶⁵Ho) в сечении реакции наблюдаются 2 резонанса, степень проявления которых зависит от деформации ядра.
    В тяжелых сферических ядрах (пример – ²⁰⁸Pb) в сечеии наблюдается один резонанс с весьма слабо выраженными структурными особенностями.
    Из данных, приведенных на Рис. 1, видно, что при переходе от легких ядер к тяжелым ГДР смещается в область меньших энергий (от ~ 17.0МэВ для ¹²C к ~ 13.5 МэВ для ²⁰⁸Pb). При этом величина ГДР увеличивается соответственно от ~ 130 до ~ 700 мбн.
    Из представленной на Рис. 1 схемы ГДР ясно, что для описания ГДР необходимо несколько основных параметров:

• положение максимума сечения Е_max;
• величина сечения в максимуме (амплитуда) резонанса (max) σ_max;
• интегральное сечение σ^инт = ∫σ(E)dE – сечение, проинтегрированное по области ГДР;
• ширина Г максимума ГДР.

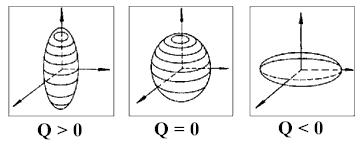
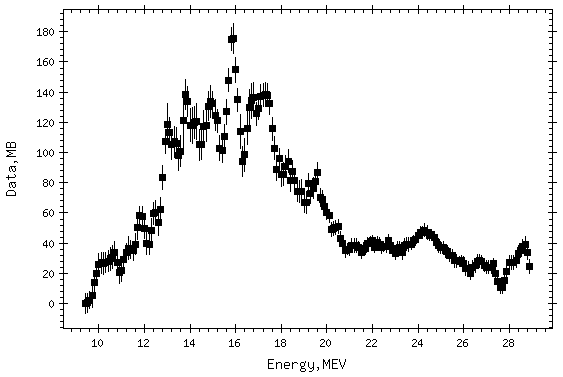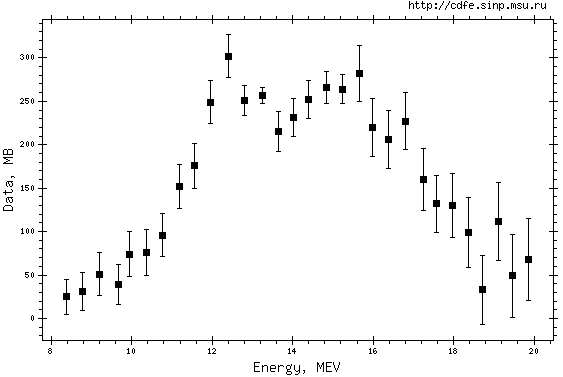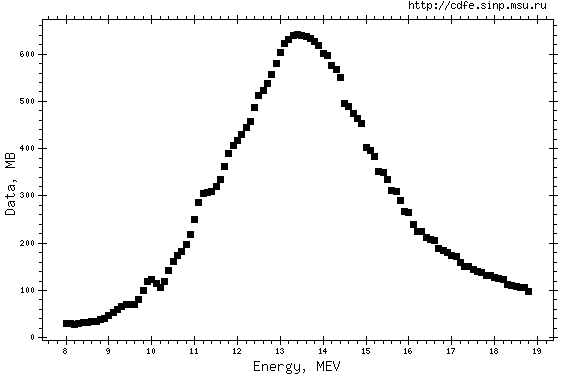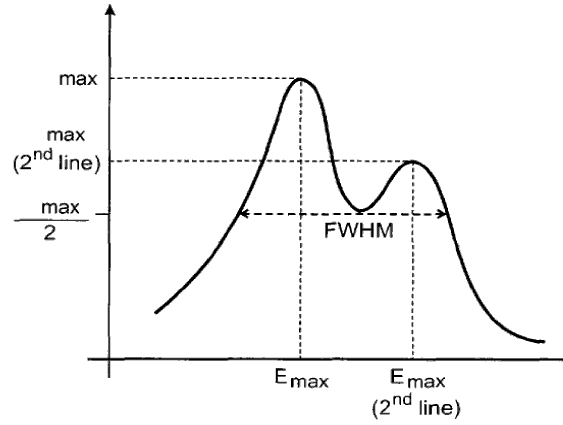Рис. 1. ГДР в сечениях реакции полного фотопоглощения (γ,abs)[2, 3] – сверху вниз: - легкое сферическое ядро 12С; - средне-тяжелое деформированное ядро 165Ho; - тяжелое сферическое ядро 208Pb; - схема ГДР (Еmax, max (σmax), Г = FWHM,…) для деформированного ядра.

3.1.1. Энергетическое положение ГДР в сферических недеформированных ядрах

    Энергетическое положение максимума ГДР Е_max для различных ядер может быть описано в рамках простых коллективных моделей, в которых предполагается, что гигантскому резонансу отвечает взаимное колебание всех протонов ядра относительно всех его нейтронов. Это описание основывалось на представлении о единой частоте колебаний нейтроной и протонной «жидкостей» при взаимодействии электрического дипольного излучения с ядром, как с целым ядерным объектом. В одних вариантах коллективной теории предполагалось, что сила, возвращающая сместившиеся жидкости к положению равновесия, пропорциональна градиенту плотности жидкостей, что приводило [5] к зависимости от массового числа А ядра Е_max ~ А^-1/3. При установлении точного количественного соотношения, которое было бы применимо ко всем ядрам, было установлено, что точность описания, как в области самых легких, так и самых тяжелых сферических ядер не очень высока:

     Наибольшее распространение получило усредненное соотношение(Рис. 3а)

    В других вариантах коллективной теории ядра предполагалось, что возвращающая сила пропорциональна площади поверхности ядра, что приводило к зависимости Е^макс ~ А^-1/6:

    Для наиболее точного описания положения ГДР было предложено следующее полуэмпирическое соотношение, объединяющее выражения (2) и (3)

    При переходе от легких ядер к тяжелым, ГДР смещается ((1)  (4)) из области энергий возбуждения ~ 15– 20 МэВ в область энергий ~ 13 – 14 МэВ (Рис. 1, 3).
    Такое положение максимума ГДР объясняет термин «дипольный» в его названии: в рассматриваемой энергетической области оказывается применимым так называемое длинноволновое приближение. Оно исходит из того, что длина волны фотона с энергией E_γ ~ 15 МэВ, близкой к энергии максимума ГДР (λ = 2πћc/E_γ ≈8·10^-12см), много больше размеров ядра
(R =1.2 A^1/3·10^-13см ≈ 7·10^-13см). Длинноволновое приближение означает, что вероятность поглощения ядром электрических дипольных фотонов должна во много раз превосходить вероятность поглощения фотонов другого типа.

ГДР в несферических деформированных ядрах.

    В несферических деформированных ядрах основной максимум ГДР расщепляется на два, расположенные при энергиях Е_max1 и Е_max2 (Рис. 1). Это получает простое объяснение в коллективных теориях: в таком ядре, в отличие от сферического, появляются два выделенных направления колебаний протонной и нейтронной жидкостей - по двум направлениям с разными частотами. Положения двух максимумов ГДР, а следовательно и величина расщепления ГДР зависят от параметра β квадрупольной деформации ядра:

    Если ядро имеет положительный электрический квадрупольный момент (Рис. 2), то есть оно вытянуто вдоль оси симметрии Z, то R_z > R_xy, и величина расщепления ΔЕ_max=Е_max2–Е_max1 должна быть пропорциональна разности (1/R₂)   (1/R_z). При этом меньшему по энергию максимуму должны соответствовать колебания вдоль длинной оси ядерного эллипсоида, а большему – вдоль короткой.
    При сильной деформации ядра по величине расщепления ΔЕ_max можно судить об эксцентриситете ε ядра, а значит и о его электрическом квадрупольном моменте β

где эксцентриситете ядра

а R – радиус сферы, объем которой равен объему ядерного эллипсоида деформированного ядра.

3.1.2. Интегральное сечение фотопоглощения

    Увеличение абсолютной величины сечения фотопоглощения с возрастанием массового числа ядра (Рис. 1, 3) от ~ 130 мбн для ядра углерода до ~ 700 мбн для ядра свинца приводит к соответствующему возрастанию интегрального сечения, которое может быть описано приблизительно по линейному закону

    Приведенное соотношение представляет собой оценку дипольного правила сумм Томаса Рейче Куна (ТРК) для интегрального сечения фотопоглощения ядром электрических дипольных фотонов, полученную в предположении об отсутствии обменных сил.

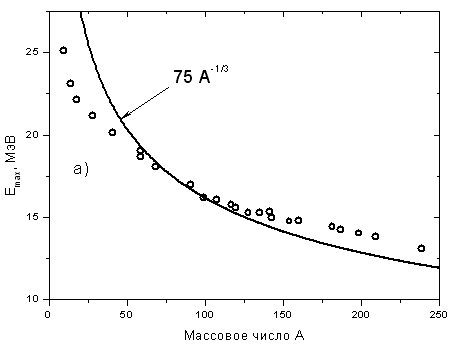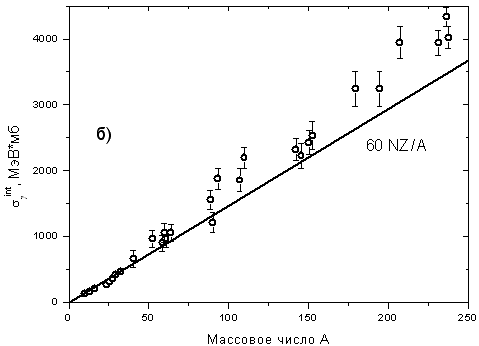Рис. 3. Зависимости положения максимума Еmax ГДР (а) и интегрального сечения реакции полного фотопоглощения (б) от массового числа ядра [5].

    Соотношение (8) хорошо подтверждает дипольный характер обсуждаемых гигантского резонанса: если бы ГДР не был преимущественно обусловлен поглощением дипольных фотонов, его интегральное сечение (а следовательно и абсолютная величина) было бы во много раз меньше величины 60 NZ/A. Следует сразу отметить, что экспериментальные данные в целом подтверждают линейную зависимость σ^инт от A (9), однако, для конкретных ядер наблюдаются довольно заметные отклонения (в обе стороны) от значения 60 NZ/A (Рис. 3б). В определенной степени это связано с существенными трудностями определения абсолютных значений сечения фотопоглощения в прямых экспериментах, а также – с некоторыми проблемами, определения сечения полного фотопоглощения как суммы сечений парциальных реакций (см. далее). Дело в том, что в отдельных случаях некоторые из составляющих реакцию фотопоглощения парциальные реакции оказываются неучтенными, тогда как, ряд других - напротив, переоцененными.

3.1.3. Ширина гигантского резонанса

    Ширина ГДР не имеет какой либо систематической зависимости от массового числа ядра А, в значительной степени зависит от формы ядра.
    Экспериментальные данные свидетельствуют о том, что ширина ГДР отражает внутреннюю структуру ядра, его форму:
- для ядер с заполненными оболочками ГДР имеет ширины, заметно меньшие, чем для ядер с незаполненными оболочками;
- ширина ГДР для магических ядер оказывается заметно меньше, чем ширина ГДР для соседних с ними изотопов и изотонов.
    Большую ширину имеет ГДР в вибрационно деформированных (мягких) ядрах. Для деформированных ядер, ГДР расщепляется на 2 резонанса, и при достаточно большом расщеплении понятие единой ширины ГДР существенно усложняется.

Ширина ГДР в мягких сферических ядрах.

    В мягких сферических ядрах ширина ГДР меняется от ~ 3 – 4 МэВ (для магических ядер) до ~ 7 – 10 МэВ и в целом достаточно хорошо описывается с помощью соотношения

Ширина ГДР в деформированных ядрах.

    Для описания зависимости ширины ГДР от его энергетического положения в случае случае деформированных ядер соотношение (10а) соответствующим образом (5, 6) модифицируется для двух проявляющихся в сечении максимумов при энергиях Е^макс_1,2

     При небольшой деформации ядра должно наблюдаться не расщепление ГДР на два максимума, а лишь некоторое увеличение его ширины

где Г – ширина ГДР недеформированного (сферического) ядра (9), а ΔГ – дополнительное уширение, пропорциональное разности (1/R_xy– 1/R_z), где R_z> R_xy– радиусы ядра соответственно вдоль оси симметрии Z и в перпендикулярном направлении. Таким образом, между шириной ГДР и величиной эксцентриситета ядра ε(8) должна быть корреляция [6, 7], что и находит свое экспериментальное подтверждение.
    В дополнение к описанному увеличению ширины (и расщеплению) ГДР, связанному со статической деформацией ядра, характерному для относительно тяжелых ядер, для средних и легких ядер существует ряд факторов, способствующих не только значительному возрастанию ширины ГДР, но и существенному усложнению его формы (проявлению отчетливых структурных особенностей). К числу наиболее важных факторов подобного рода следует в первую очередь отнести эффекты конфигурационного и изоспинового расщепления ГДР. Последнее обстоятельство, в свою очередь, во многих случаях усложняет процедуру определения самой ширины ГДР.

3.2. Основные каналы распада гигантского дипольного резонанса

    Процесс поглощения ядром γ кванта с энергией, характерной для ГДР (до ~ 50 МэВ), приводит к испусканию отдельных нуклонов и их комбинаций. Ядро с наибольшей вероятностью испускает 1 нуклон, с меньшей вероятностью – 2, с еще меньшей – 3 и т.д. Это обстоятельство вместе с соотношением энергий, необходимых для выбивания того или иного количества нуклонов (энергетических порогов соответствующих реакций) из ядра, определяет основные каналы распада ГДР. Представление об основных каналах распада ГДР и областях энергий, в которых эти каналы проявляются, дает Таблица 1 Главы 1, в которой для примера приведены пороги нескольких наиболее вероятных парциальных фотоядерных
реакций для нескольких ядер различного атомного веса.
    Реакция, соответствующая каналу распада ГДР с вылетом нуклона или их комбинаций, называется парциальной. Как было показано, ядерная реакция полного фотопоглощения включает в себя (соотношение (13) Главы 1) парциальные реакции всех возможных каналов выбывания фотонов из первичного пучка - (γ,n), (γ,np), (γ,2n), (γ,3n), (γ,1p), (γ,2p), (γ,t), (γ,d), (γ,α), …,(γ,f). При этом в экспериментах, как правило, определяются сечения полных реакций, таких как фотонейтронная (γ,xn) (соотношение (20) Главы 1) и фотопротннная (γ,xp) (соотношение (27) Главы 1). Сечения парциальных реакций, например, фотонейтронных для ядра ¹¹⁹Sn (Рис. 4), также имеют форму резонансов, которые располагаются в той же энергетической области, однако из за порога сдвинуты относительно максимума в сечении реакции полного фотопоглощения.
    Наибольший вклад в сечение фотопоглощения в области энергий максимума ГДР для легких и средних ядер дают реакции (γ,n) и (γ,p), в тяжелых ядрах доминирует вклад фотонейтронного канала. Положение максимума в сечении парциальной реакции (γ,n) для многих ядер совпадает с максимумом сечения реакции полного фотопоглощения. В средних и тяжелых ядрах максимум сечения фотопротонной реакции расположен при больших энергиях (Рис. 5), а абсолютная величина сечения фотопротонной реакции, как правило, меньше абсолютной величины сечения фотонейтронной реакции, в лнгких ядрах картина сложнее.
    За максимумом ГДР начинают проявляться вклады двухнейтронной реакции (γ,2n), двухнуклонной реакции (γ,np), а также реакции (γ,3n), энергетические пороги которых достаточно высоки.

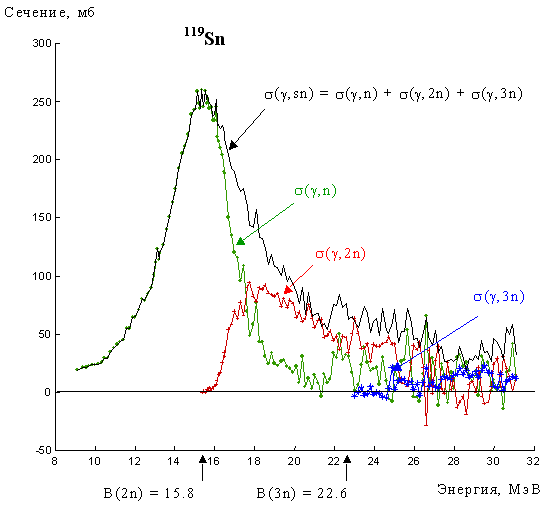Рис. 4. Взаимное расположение максимумов в сечениях парциальных фотонейтронных реакций на ядре 119Sn.

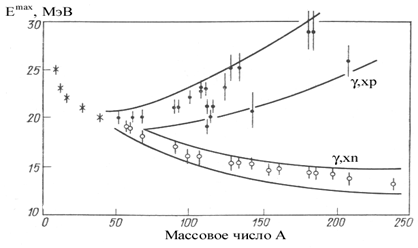Рис. 5. Энергетические положения максимумов сечений полной фотонейтронной (γ,xn) реакции (светлые) и полной фотопротонной (γ,xp) реакции (темные точки) в зависимости от массового числа А ядра мишени.

    Из сказанного ясно, сколь серьезную проблему представляет собой разделение каналов распада ГДР. Однозначное выделение определенного канала возможно при использовании некоторых специальных методов, прежде всего, метода наведенной активности, позволяющем идентифицировать конечное ядро по характерному радиоактивному излучению. Однако, как было показано в Главе 1, этот метод может быть использован далеко не всегда, поскольку многие конечные ядра реакций либо имеют неподходящие характеристики радиоактивного излучения, либо оказываются и стабильными. Техника совпадений для регистрации нескольких частиц-продуктов в условиях относительно небольших абсолютных величин сечений также не дает возможности исследовать отдельные каналы распада ГДР с достаточно высокой точностью.
    Наибольшее распространение получил метод прямой регистрации продуктов реакций при использовании специальных методик разделения реакций по множественности. Поскольку при его применении вклад реакции с образованием двух нейтронов будет удваиваться, трех – утраиваться и т.д., требования к процедуре разделения продуктов реакций по множественности оказываются очень высокими и, как показывает практика (см. далее) не всегда достигаемыми.

3.3. Основные проблемы теоретической интерпретации гигантского дипольного резонанса

3.3.1. Проблемы описания структуры

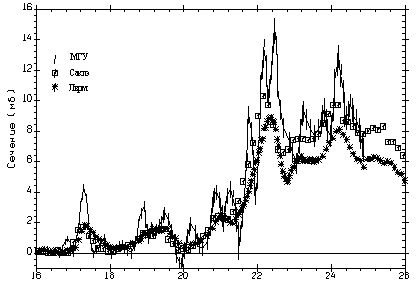Рис. 6. Сравнение сечений реакции 16O(γ,xn), полученных в разных экспериментах при близких значениях энергетического разрешения: точки с ошибками - эксперимент, выполненный в МГУ на пучке тормозного -излучения энергетическое разрешение Δ= 200 кэВ; квадраты - эксперимент, выполненный на пучке квазимоноэнергетических аннигиляционных фотонов в Сакле (Франция) [26], Δ = 180 – 280 кэВ; звёздочки – аналогичный эксперимент, выполненный в Ливерморе (США), Δ = 200 – 300 кэВ.

    Как было отмечено выше, положение по энергии и общая форма ГДР как в сферических, так и в деформированных ядрах достаточно хорошо описываются в рамках простейших коллективных моделей ядра [8].
    Однако ни одна из них не претендует на описание наблюдаемых экспериментально структурных особенностей ГДР – значительного количества резонансов различной ширины и формы, часто распределенных в области энергий, ширина которых достигает (а в отдельных случаях превышает) 10 МэВ. Эксперименты, выполненные с достаточно высоким энергетическим разрешением, выявляют структуру ГДР трех видов – грубую (гросс), промежуточную и тонкую.
    Такие структурные особенности отчетливо проявляются, например, в случае реакции ¹⁶O(,xn), 3 сечения для которой, определенные разными методами, приведены на Рис. 6. Видны особенности с шириной ~ 5 МэВ (собственно ГДР, расположенный при энергии около 24 МэВ), с шириной ~ 1 МэВ (резонансы при энергиях ~ 17, 19, 21, 23, 25 МэВ) и с шириной ~ 100 кэВ.

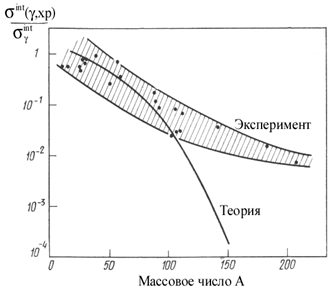Рис. 7. Экспериментальная и предсказываемая статистической теорией зависимости от массового числа А ядра мишени относительного вклада сечения фотопротонной реакции в полное сечение фотопоглощения [5] .

    Кроме того, определенные трудности возникают при описании с их помощью распадных характеристик гигантского резонанса:

• экспериментальные выходы фотопротонов [5] в тяжелых ядрах (Рис. 7) превышают предсказываемые статистической теорией в 10² - 10³ раз;
• совершенно не описываются большая ширина и сложная форма (промежуточная и тонкая структура) ГДР;
• фотонуклонные спектры существенно отличаются от статистических по форме;
• угловые распределения фотонуклонов, как правило, не являются изотропными, как того требует статистическая теория.

    Необходимость преодоления указанных трудностей потребовала разработки сначала одночастичной, а затем многочастичной модели оболочек [9, 10]. Последняя, предсказывая появление сильных когерентных Е1 возбуждений в области энергий существенно больших, чем энергии одночастичных электрических дипольных колебаний, оказывается в состоянии правильно описать энергетическое положение ГДР.
    При этом форма ГДР описывается лишь приблизительно: предсказываемый спектр Е1 возбуждений оказывается чрезвычайно бедным (учет остаточного взаимодействия приводит, как правило, к формированию одного – двух когерентных (коллективных) состояний, исчерпывающих практически всю дипольную сумму). Развитие модели путем дополнения обычных возбуждений типа «одна частица – одна дырка (1p - 1h), многочастично многодырочными возбуждениями, расширения их возможного базиса путем единого описания различных коллективных движений (вращений, поверхностных колебаний, дипольных колебаний ядра), а также взаимодействий между ними позволило приблизиться к описанию структуры ГДР.
    На основании сказанного можно сделать заключение о том, что коллективные входные 1p - 1h состояния определяют гросс-структуру (ширины ~ несколько МэВ) ГДР, связь входных состояний с более сложными состояниями коллективного характера приводит к формированию резонансов (с шириной ~ МэВ) промежуточной структуры ГДР, а взаимодействие входных состояний ядра с неколлективными многочастично многодырочными возбуждениями - к появлению резонансов с шириной ~ 100 кэВ.

3.3.2. Проблемы описания ширины

    Несмотря на очевидные успехи современных коллективных и микроскопических моделей в описании ГДР, интерпретация его формы и большой ширины далека от завершения. Это обусловлено целым рядом обстоятельств, из которых следует отметить большие вычислительные трудности и отсутствие до сих пор достоверной информации о ряде важных параметров теории.
    Вместе с тем большое значение для описания наблюдаемых экспериментально параметров ГДР, его проявлений в сечениях различных парциальных реакций, соотношений вероятностей различных каналов распада имеют эффекты, обусловленные различием конфигурационной структуры ядерных оболочек и действием правил отбора по изоспину.

Конфигурационное расщепление гигантских дипольных резонансов.

    Суть концепции конфигурационного расщепления [11] ГДР, наиболее ярко проявляется в области легких (A ≤ 40) ядер. Она заключается в том, что в таких ядрах, в отличие от средних и тяжелых, не формируется узкий пик, отвечающий коллективным колебаниям всех протонов ядра относительно всех его нейтронов с некоторой единой частотой. Дипольные колебания в значительной степени утрачивают коллективную природу.
    Интенсивное дипольное поглощение фотонов происходит не в области единого максимума ГДР, а в достаточно широкой (10 – 20 МэВ) области энергий. При этом фотоны из области меньших энергий формируют ветвь “I” (низкоэнергетичная компонента σ_нэ) ГДР, обусловленную переходами нуклонов из внешней частично заполненной оболочки в ближайшую свободную оболочку. Фотоны из области больших энергий формируют ветвь “II” (высокоэнергетичная компонента σ_вэ), обусловленную переходами нуклонов из внутренней заполненной оболочки во внешнюю частично заполненную. Физическая причина такого расщепления ГДР заключается в том, что в легких ядрах заметную роль играет пространственно обменная часть нуклон нуклонного взаимодействия. Благодаря действию пространственно обменных сил и нелокальности нуклон нуклонного взаимодействия и возникает сильный сдвиг по энергии глубоких дырочных состояний, отвечающих внутренним заполненным оболочкам ядра.
    На Рис. 8 приведена схема конфигурационного расщепления ГДР легкого ядра ⁷Li, для которого оно должно иметь величину ~ 10 МэВ.
    Наиболее ярким проявлением эффектов конфигурационного расщепления является заметное различие энергий фотонуклонов, соответствующих двум указанным группам переходов. На Рис. 9 для ядра ⁷Li представлены реакции, в котроых проявляются обе компоненты расщепления.
    Слева перечислены реакции компоненты «I» - в них не происходит разрушения кора ядра лития – ядра гелия или α-частицы, и она присутствует среди продуктов реакций. Справа перечислены реакции компонеты «II» - в них α-частица разрушается, и среди продуктов реакций отсутствует.
    Следует отметить, что и для более тяжелых ядер, например, ядер 1f-2p оболочки величина расщепления, обусловленного этими эффектами, может достигать нескольких МэВ, а для ядер 1s оболочки – десятка МэВ.

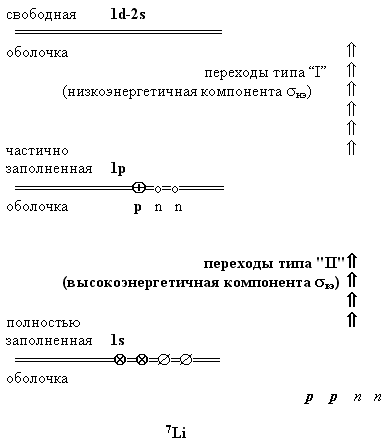Рис. 8. Схема конфигурационного расщепления ГДР ядра 7Li.

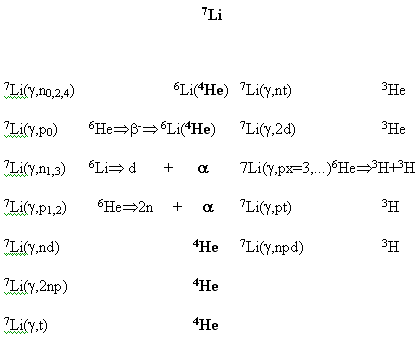Рис. 9. Перечень реакций, формирующих 2 конфигурационные компонеты ГДР ядра 7Li. Слева – реакции компоненты «I», справа – компоненты «II».

    С одной стороны, распад высоковозбужденных состояний гигантского резонанса ядра (N, Z) с изоспином T_> по нейтронному каналу на основной и низколежащие уровни конечного ядра (N   1, Z) запрещен правилами отбора по изоспину, поскольку нейтрон, уносящий изоспин ½, не может оставить конечное ядро в состоянии с изоспином T = T₀ - 1/2.
    С другой стороны, распад уровней гигантского резонанса, имеющих изоспин T_<, по протонному каналу на состояния конечного ядра (N, Z - 1) по сравнению с распадом более высоко расположенных уровней с изоспином T_> сильно подавляется кулоновским барьером ядра. Таким образом, распад состояний гигантского с изоспином T_< должен идти преимущественно по нейтронному каналу, а с изоспином T_> – по протонному: гигантский резонанс с T_> будет проявлять себя главным образом в фотопротонной реакции, а гигантский резонанс с T_< – в фотонейтронной.Для детального изучения таких эффектов необходима информация не только об энергетических спектрах выбиваемых фотонуклонов, но и о парциальных и полных сечениях реакций с их образованием: необходимо знать не только с какого именно состояния возбужденного ядра испускается нуклон определенной энергии, но и на какое состояние конечного ядра происходит этот переход. Поскольку заселение ядерных оболочек протонами и нейтронами происходит по-разному, для детального изучения эффектов конфигурационного расщепления ГДР необходима информация об обоих каналах его распада.

Изоспиновое расщепление гигантских дипольных резонансов.

    В начале шестидесятых годов было установлено, что изоспин является хорошим квантовым числом. Тот факт, что состояния ядра характеризуются определенным значением изоспина, существенным образом сказывается на особенностях различных ядерных реакций, в том числе и реакций, вызываемых электромагнитным излучением. Суть концепции изоспинового расщепления ГДР [12 - 14] наиболее ярко проявляющегося в области средних и тяжелых ядер, заключается в следующем. В соответствии с правилами отбора по изоспину, в ядрах с N = Z конечными состояниями будут являться состояния с одним значением изоспина Т = 1. При взаимодействии налетающих γ квантов с ядром, имеющим изоспин основного состояния Т₀ = (N   Z)/2 ≠ 0, в нем происходит (Рис. 10) возбуждение двух групп уровней с изоспинами Т_< = Т₀ и T_> = Т₀ + 1, которые концентрируются при разных энергиях возбуждения.
    Центр гигантского резонанса с T_> располагается при более высоких энергиях, чем центр тяжести гигантского резонанса с T_<. Это позволяет более правильно описать ширину ГДР.

3.3.3. Проблемы описания интегрального сечения фотопоглощения

    Несмотря на то, что предсказания дипольного правила сумм (9) считаются вполне удовлетворительными оценками абсолютных величин ГДР (12), сравнение конкретных значений [15] интегральных сечений реакций (γ,sn), (γ,p) и (γ,abs) – соответственно σ^инт(sn), σ^инт(p) и σ^инт(abs) – с такими предсказаниями (Таблица 1) выявляют весьма пеструю картину.

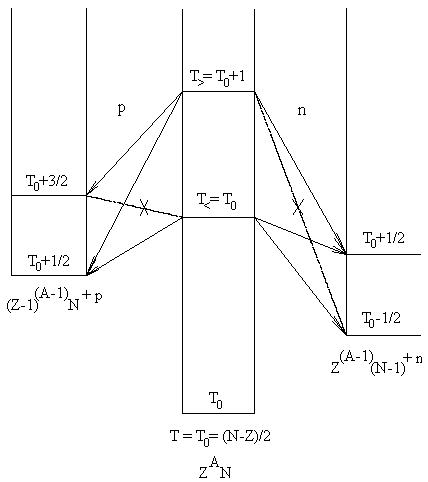Рис. 10. Схема возбуждения и распада по нейтронному и протонному каналам состояний ГДР с различными значениями изоспина (пунктир – переходы, запрещенные законом сохранения изоспина).

Таблица 1.

Сравнение величин [15] интегральных сечений реакций (γ,sn), (γ,p) и (γ,abs) – соответственно σ^инт(sn), σ^инт(p) и σ^инт(abs) – с предсказаниями дипольного правила сумм.

    В то время, как для одних ядер действительно наблюдается удовлетворительное согласие, для других обнаруживаются существенные расхождения, причем как в одну, так и другую сторону.
    Следует отметить, что имеется большое количество случаев, когда экспериментальные величины ГДР заметно превышают оценки дипольного правила сумм. Эти расхождения оказываются настолько значительными, что для их объяснения в ряде теоретических исследований было введено понятие эффективной массы нуклона внутри ядра, отличающейся от массы нуклона в свободном состоянии.
    Детальный анализ приведенных данных выявляет их вполне определенную зависимость от способа получения. Так, например, абсолютные значения сечений фотопоглощения, полученных в экспериментах с тормозным γ-излучением, отличаются от результатов экспериментов, выполненных на пучках квазимоноэнергетических аннигиляционных фотонов.
    Более того, сравнение данных и того и другого типа, полученных в разных лабораториях, также отличаются друг от друга. Очевидно, что подобные расхождения являются следствием присутствия в данных неучтенных систематических погрешностей. Определение их величины и степени вляния на результат измерений, разработка методов их учета существенно меняют ситуацию с оценкой абсолютной величины ГДР.
    Более подробно описание основных характеристик ГДР может быть получено в работах [16 – 21].

Литература к Главе 3

1. E.G.Fuller, H.Gerstenberg. Photonuclear Data – Abstracts Sheets 1955 - 1982. NBSIR 83-2742. U.S.A. National Bureau of Standards, 1986.
2. В.В.Варламов, В.В.Сапуненко, М.Е.Степанов. Фотоядерные данные 1976 - 1995. Указатель. Издательство Московского университета, -M., 1996.
3. S.S.Dietrich, B.L.Berman. Atomic Data and Nuclear Data Tables, 38 (1988) 199.

4. A.V.Varlamov, V.V.Varlamov, D.S.Rudenko, M.E.Stepanov. Atlas of Giant Dipole Resonances. Parameters and Graphs of Photonuclear Reaction Cross Sections. INDC(NDS)-394, IAEA NDS, Vienna, Austria, 1999.
5. Б.С.Ишханов, И.М.Капитонов. Взаимодействие электромагнитного излучения с атомными ядрами. Издательство Московского университета. Москва, 1979.
6. M.Danos. On the long-range correlation model of the photonuclear effect. Nucl.Phys., 5 (1958) 23.
7. K.Okamoto. Intrinsic quadrupole moment and the resonance width of photonuclear reactions. Phys.Rev., 110 (1958) 143.
8. D.H.Wilkinson. Nuclear Photodisintegration. Physica, 22 (1956) 1039.
9. J.P.Elliot, B.H.Flowers. The Odd-Parity States of ¹⁶O and ¹⁶N. Proc.Roy.Soc., A242 (1957) 57.
10. G.E.Brown, M.Boisterli. Dipole States in Nuclei. Phys.Rev.Lett., 3 (1959) 472.
11. Б.С.Ишханов, И.М.Капитонов, В.Г.Неудачин, В.Г.Шевченко, Р.А.Эрамжян, Н.П.Юдин. Конфигурационное расщепление дипольного гигантского резонанса в атомных ядрах. Препринт ИЯИ АН СССР, П-0578, Москва, 1988.
12. H.Morinaga. Phys. Rev., 97 (1955) 444.
13. R.O.Akyuz, S.Fallieros. Phys. Rev. Lett., 27 (1971) 1016.
14. S.Fallieros, B.Goulard, R.H.Venter. Phys. Lett., 19 (1965) 398.
15. База данных по ядерным реакциям (http://cdfe.sinp.msu.ru/exfor/index.php)
16. А.Б.Мигдал. ЖЭТФ, 15 (1945) 81.
17. M.Goldhaber, E.Teller. Phys. Rev., 74 (1948) 1046.

18. H.Steinwedel, Y.D.Jensen. Z.Naturforsch, 5A (1950) 413.

19. О.Бор, Б.Моттельсон. Структура атомного ядра. Издательство «Мир», Москва, 1977.
20. Л.Валантэн. Субатомная физика: ядра и элементарные частицы. Издательство «Мир», Москва, 1986.
21. Дж.Левинджер. Фотоядерные реакции. Издательство иностранной литературы, Москва, 1962.

---