Глава 4.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
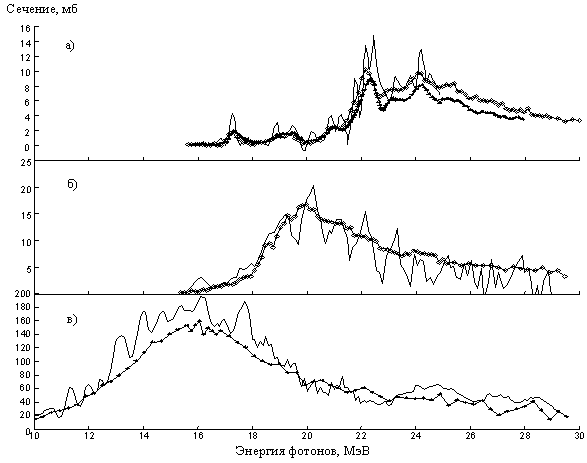 Рис. 1. Сравнение между собой сечений однотипных реакций, полученных в ТИ- (сплошные линии) и КМА- (кресты и ромбы) экспериментах: а) реакция 16O(γ,хn); б) реакция 40Ca[(γ,n) + (γ,np)]; в) реакция 107Ag(γ,хn). |
Важно подчеркнуть, что, поскольку обсуждаемые особенности сечений реакций, получаемых в различных экспериментах, однозначно связаны с их типом, они – расхождения - имеют систематическую природу. Не менее важно отметить, что наблюдаемык систематические расхождения результатов различных экспериментов превосходят достигнутые в них статистические погрешности.
4.1. Данные по сечению полной фотонейтронной реакции (γ,хn)
4.1.1. Структура сечения реакции (энергетическое разрешение)
Реакция 16O(γ,хn).
Типичный
пример обсуждаемых расхождений – сравнение результатов трех
экспериментов по определению сечения полной фотонейтронной реакции
16O(γ,хn)
из одного ТИ [5] и двух КМА экспериментов [6, 7],
представленных на Рис. 1а – с большей детализацией приводится
на Рис. 2. Хорошо видно, что надёжно разделенные мощные максимумы,
располагающиеся при близких значениях энергии, наблюдаются во всех
трёх сравниваемых сечениях, полученных при близких значениях
заявленного энергетического разрешения ([5]: 200 кэВ, [6]: 180 –
200 кэВ, [7]: 200 – 300 кэВ).
По
форме и по абсолютной величине соответствующие резонансы различаются,
причём все резонансы в обоих КМА сечениях имеют величины
меньшие, а ширины большие по сравнению с резонансами в ТИ сечении.
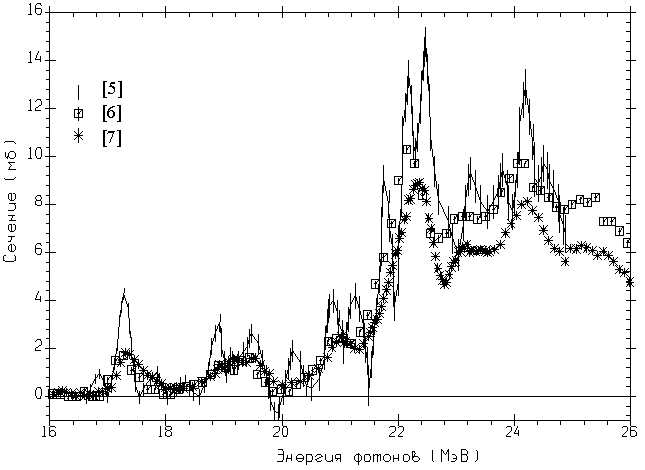 Рис. 2. Сравнение сечений реакции 16O(γ,xn), полученных в разных экспериментах при близких значениях энергетического разрешения: точки с ошибками – ТИ эксперимент, выполненный в Московском университете (Россия) [5], энергетическое разрешение Δ = 200 кэВ; квадраты – КМА эксперимент, выполненный в Саклэ (Франция) [6], Δ = 180 – 280 кэВ; звёздочки – КМА эксперимент, выполненный в Ливерморе (США) [7], Δ = 200 – 300 кэВ. |
Это представляется вполне естественным, если сравнить
между собой соответствующие типичные эффективные спектры фотонов
(аппаратные функции), представленные на Рис. 4 Главы 1.
Важно отметить, что
абсолютные значения ТИ сечения [5] и КМА сечения Саклэ [6]
близки: интегральные сечения, рассчитанные для общих пределов
интегрирования составляют 36.90 и 34.52 МэВ·мб
(КМА сечение Саклэ выглядит как сглаженная версия ТИ сечения).
В то же
время КМА сечение Ливермора [7] значительно отличается по
величине от двух других и приближается к ним лишь после умножения на
некий коэффициент (31.01 = 1.12 х 27.64 МэВ·мб;
происхождение дополнительного нормировочного множителя 1.12 будет
обсуждаться ниже).
Эти
расхождения могут быть обусловлены не только сглаженностью сечений
реакций, но другими причинами, такими как, например, различия
(погрешности) процедур определения интенсивности фотонного пучка
и/или эффективности детектора нейтронов.
Реакция 18O(γ,хn).
Для того, чтобы выяснить природу наблюдавшихся расхождений, было проведено несколько специальных исследований. Одним из них является детальное сравнение [8] сечений полной фотонейтронной реакции на изотопе кислорода 18O(γ,xn). Анализировались параметры резонансов, обнаруженных [8] в ТИ эксперименте (Австралия, Мельбурн) и КМА эксперименте (Ливермора) [9]. Авторы работы [8] говорят о хорошем согласии данных, однако из их собственного анализа следует очевидный вывод о том, что оба сечения заметно расходятся (Таблица 1).
Таблица 1.
Сравнение параметров (энергия E, амплитуда A, ширина Г) структурных особенностей сечений реакции 18O(γ,xn), полученных с помощью пучков тормозного γ излучения и квазимоноэнергетических фотонов.
| ТИ эксперимент [8] | КМА эксперимент [9] | Отношения амплитуд и ширин | |||||
|
E, МэВ |
А, мбн |
Г, МэВ |
E, МэВ |
A, мбн |
Г, МэВ |
АТИ/АКМА, отн.ед. |
ГКМА/ГТИ, отн.ед. |
| 9.1 | 1.4 | 0.4 | 9.1 | 1.1 |
0.6 |
1.27 |
1.50 |
| 10.4 | 6.5 | 0.4 | 10.3 | 5.3 |
0.9 |
1.27 |
2.25 |
| 11.6 | 11.5 | 0.6 | 11.5 | 9.0 |
0.7 |
1.28 |
1.17 |
| 13.2 | 8.5 | 0.6 | 13.1 | 8.6 |
0.7 |
1.00 |
1.17 |
| 14.0 | 8.5 | 0.6 | 13.8 | 6.9 |
0.6 |
1.23 |
1.00 |
| 14.8 | 14.0 | 0.6 | 14.8 | 13.1 |
0.8 |
1.07 |
1.33 |
| 15.8 | 13.0 | 0.7 | 15.8 | 10.9 |
0.7 |
1.19 |
1.00 |
| 17.6 | 10.5 | 17.2 |
10.1 |
|
1.04 |
|
|
| 19.3 | 12.0 | 0.6 | 19.1 | 10.0 |
|
1.20 |
|
| 23.6 | 21.0 | 1.8 | 23.7 | 17.7 |
2.5 |
1.19 |
1.39 |
|
Среднее значение <АТИ/АКМА> |
Среднее значение <ГКМА/ГТИ> |
1.17 |
1.35 |
||||
При
всей условности процедуры определения ширин и амплитуд резонансов в
сечениях, имеющих сложную структуру, практически все резонансы в
КМА сечении имеют меньшие амплитуды и большие ширины, чем
резонансы в ТИ сечении, да и надежно выявленных резоансов в
ТИ сечении больше, чем в КМА сечении.
Соответствующие
средние значения отношений составляют <АТИ/АКМИ>
= 1.17 и
<ГКМА/ГТИ>
= 1.35. При этом интегральные сечения для области энергий 8 –
28 МэВ также различаются: σинтТИ
= 187.12 МэВ·мб
и σинтКМА
= 167.33 МэВ·мб
(а их отношение оказывается вновь весьма близким к уже упомянутому
выше значению 1.12).
Для
количественного сравнения формы сечений реакций, полученных в разных
экспериментах (свыше 250 наборов данных для ядер от 3H
до 238U), был
введен [10] специальный параметр «структурность» S,
описывающий степень отклонения определенного сечения от того же
самого сечения, но сглаженного на некотором инервале энергий (1 МэВ):
|
|
(1) |
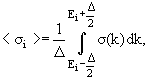 |
(2) |
|
|
(3) |
где Δ – шаг
сглаживания (1 МэВ), D – общая
область энергии, в которых определены сравниваемые сечения
реакции
С
целью исследования того, насколько близкую форму имеют сильно
сглаженные сечения разных лабораторий, при использовании введенного
параметра структурности S, была получена [10] общая систематика
данных по соотношению параметров структурности, рассчитанных по
данным различных экспериментов.
На
Рис. 3 представлены отношения S/SL,
в которых структурность S рассчитывалась по данным различных
лабораторий, а структурность SL
– по КМА данным Ливермора (в случаях, когда данные
Ливермора отсутствуют, использовались данные других КМА лабораторий.
Такие
отношения рассматривались потому, что для рассмотрения
систематических различий отдельных экспериментов следует приводить
данные различных типов к данным какого либо одного типа,
выбранного в качестве своеобразного “эталона”. Выбор в
качестве такого “эталона” данных из Ливермора не означает
их какого либо приоритета перед другими и обусловлен лишь тем
обстоятельством, что наибольшее количество КМА данных было
получено именно в Ливерморе.
Из
Рис. 3 видно, что все данные достаточно отчётливо разделяются на две
группы: ТИ данные (среднее значение <S/SL>
= 4.35) и КМА данные (среднее значение <S/SL>
= 1.22). Близость последнего среднего значения к 1 означает, что для
всех трёх КМА лабораторий (Ливермор, Саклэ, Гессен) заявляемые
оценки энергетического разрешения по расчётной ширине аннигиляционной
линии (во многих случаях: 250 – 400 кэВ, в некоторых: 500 кэВ,
в нескольких: 150 – 300 кэВ) не соответствуют реальному
разрешению, достигаемому в эксперименте: все они в той или иной
степени оказываются близкими к использованному шагу сглаживания –
1 МэВ.
Эти
данные могут быть сопоставлены с независимыми результатами
экспериментов совершенно иного типа, выполненных в Иллинойсе [11, 12]
на пучках меченых фотонов (МФ), аппаратная функция для которых близка
к гауссиану. По величине анализируемого параметра S/SL
такие данные существенно превосходят КМА данные, оказываясь
весьма близкими к ТИ данным (среднее значение <S/SL>
= 4.22).
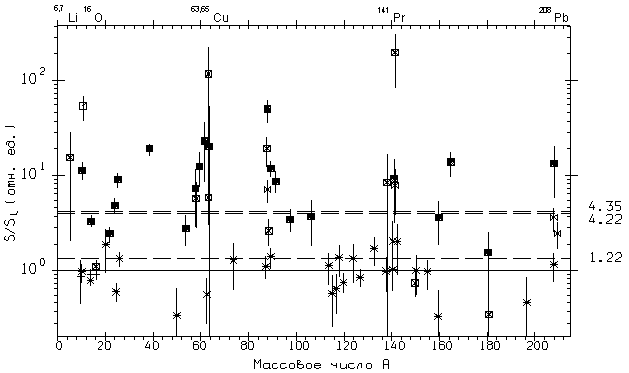 Рис. 3. Систематика данных о величине параметра S/SL для сечений полной фотонейтронной реакции: ТИ данные ( МФ данные ( |
Эта
близость ТИ и МФ данных по значениям параметра S/SL
означает, что они существенно лучше по сравнению с КМА данными
отражают реальную структуру сечений реакций, тогда как структура
сечений, полученных в КМА экспериментах оказывается существенно
сглаженной.
Такой
результат представляется вполне естественным, поскольку, как
отмечалось выше (соотношение (14) Главы 1), результат
КМА эксперимента представляет собой по существу не собственно
сечение реакции, а лишь её выход – интеграл (соотношение (1)
Главы 1) от произведения сечения реакции и аппаратной функции очень
сложной формы и достаточно протяжённой по энергии. Для того, чтобы
получить из результата КМА эксперимента сечение реакции, он
должен быть подвергнут дополнительной обработке.
Такой
обработкой может быть [13] процедура восстановления (“unfolding”)
сечения реакции из её выхода, аналогичная тем, которые применяются в
ТИ экспериментах, или метод, учитывающей реальную форму
аппаратной функции эксперимента. Как упоминалось в Главе 1, во многих
исследованиях, выполненных ранее [13 -19], для такого рода
обработки использовался (см. далее) метод редукции [20, 21], который
позволяет преобразовать результат конкретного эксперипента,
полученный при определенной форме аппаратной функции, к виду,
который этот результат может иметь, будучи полученным в
эксперименте с аппаратной функцией иной формы (см. далее Главу 5).
4.1.2. Абсолютная величина сечения реакции
Данные по интегральным сечениям.
Сравнение
результатов многочисленных исследований [5 – 9, 13 – 19],
выполненных в различных экспериментах свидетельствует о том, что
между сечениями фотонейтронных реакций, полученными в экспериментах
одного типа в разных лабораториях, наблюдаются очевидные расхождения,
причём и по абсолютной величине (Рис. 2) и по форме (Рис. 3). Это
справедливо не только для ТИ , но и для КМА экспериментов.
Если первое нисколько не удивительно вследствие большого разнообразия
методов извлечения информации о сечении реакции из её
экспериментального выхода, то второе вызывает
определенное удивление, поскольку данных
о сечениях фотонейтронных реакций в Ливерморе и Саклэ получались в
однотипных экспериментах с одинаковой методикой получения
квазимоноэнергетических аннигиляционных фотонов и высокоэффективными
детекторами прямой регистрации нейтронов.
В
качестве наглядного количественного примера расхождений по абсолютной
величине сечений однотипных реакций в Таблице 2 представлены данные
[3] Ливермора и Саклэ по интегральным сечениям
полной фотонейтронной реакции (γ,xn)
для 5 ядер.
Данные
именно для этих 5 ядер подобраны лишь по соображениям наглядности
из за близости пределов интегрирования Eγинт-макс
(они или равны в Саклэ и Ливерморе, или имеют в Ливерморе большие
значения) или самих значений интегральных сечений (подобных примеров
имеется [3] очень много, все они столь же убедительны, но менее
наглядны). Приведенные данные свидетельствуют о том, что значения Саклэ превышают соответствующие значения Ливермора более на 6 –
16 % и
более (для случая ядра 133Cs
отношение близко к 1, однако в этом случае пределы интегрирования
различаются более, чем на 5 МэВ).
Таблица 2
Сравнение величин интегральных сечений (по данным [3]) реакции (γ,xn), полученных в КМА экспериментах в Саклэ (верхние значения) и Ливерморе (нижние значения) и их отношений.
| Ядро | 51V | 75As | 90Zr | 133Cs | 165Ho |
|
Eγмакс, МэВ |
27.8 27.8 |
26.2 29.5 |
25.9 27.6 |
24.2 29.5 |
26.8 28.9 |
|
σint, МэВ·мбн |
689 654 |
1306 1130 |
1309 1158 |
2484 2505 |
3667 3385 |
| Отношение | 1.06 | > 1.16 | > 1.13 | > 1.00 | > 1.08 |
Детально и системно расхождения данных, полученных в Ливерморе и Саклэ были впервые исследованы в работах [22, 23], в которых одновременно анализировались энергетические положения и абсолютные величины сечений полной фотонейтронной реакции (γ,хn), полученных непосредственно в экспериментах, а также и сечений парциальных реакций (γ,n) и (γ,2n) для 12 средних и тяжелых ядер от 89Y до 208Pb. В Таблице 3 для всех расммотренных ядер приведены данные [3] по соотношению интегральных сечений всех трех фотонейтронных реакций.
Таблица 3.
Сравнение [22, 23] отношений (Саклэ/Ливермор) интегральных сечений [3] реакций (γ,n), (γ,2n) и (γ,хn) – соответственно Rint(n), Rint(2n) и Rint(xn).
| Ядро | Rint(n) | Rint(2n) | Rint(xn) |
| 89Y | 1.33 (1279/960) | 0.75 (74/99) | 1.26 |
| 115In | 1.09 (1470/1354) | 0.55 (278/508) | 0.94 |
| 117Sn | 0.97 (1334/1380) | 0.46 (220/476) | 1.01 |
| 118Sn | 1.06 (1377/1302) | 0.59 (258/531) | 1.06 |
| 120Sn | 0.98 (1371/1389) | 0.75 (399/673) | 0.99 |
| 124Sn | 0.82 (1056/1285) | 0.75 (502/670) | 0.93 |
| 133Cs | 1.24 (1828/1475) | 0.65 (328/503) | 1.11 |
| 159Tb | 1.37 (1936/1413) | 0.68 (605/887) | 1.06 |
| 165Ho | 1.20 (2090/1735) | 1.03 (766/744) | 1.14 |
| 181Ta | 1.68 (2180/1300) | 0.90 (790/881) | 1.22 |
| 197Au | 1.18 (2588/2190) | 0.62 (479/777) | 1.00 |
| 208Pb | 1.54 (2731/1776) | 0.38 (328/860) | 1.30 |
Были установлены следующие закономерности:
- сечения полной фотонейтронной реакции (γ,хn), полученные в Саклэ и Ливерморе, оказываются сдвинутыми друг относительно друга по энергии;
- сечения реакции (γ,хn), полученные в Саклэ, оказываются по абсолютной величине на ~ 8 – 15 % больше сечений, полученных в Ливерморе;
- величины сечений реакций (γ,n) и (γ,2n), полученные в Саклэ и Ливерморе, соотносятся между собой существенно иначе (детально ситуция будет рассмотрена далее);
- величины сечений реакций (γ,n), полученных в Саклэ, в целом также оказываются больше величин сечений, полученных в Ливерморе, однако их отношение намного превышает 10 – 15 % расхождения между величинами сечений реакций (γ,хn);
- величины сечений реакций (γ,2n) оказываются связанными между собой в обратном соотношении.
Значительные
расхождения однотипных данных по абсолютной величине были предметом
многих исследований, в том числе и выполненных самими участниками
экспериментов на пучках квазимоноэнергетических аннигиляционных
фотонов.
Наиболее
детальное из них было проведено в [24]. Сечения фотонейтронных
реакций на ядрах естZr,
127I, 141Pr,
197Au и естPb,
полученные в Ливерморе ранее, были специально повторно измерены при
энергиях вблизи максимума ГДР именно с целью выяснения возможных
причин и способов устранения их расхождений с сечениями Саклэ. Новые
данные по абсолютным величинам сечений фотонейтронных реакций для
ядер естZr,
127I, 141Pr,
197Au и естPb
детально сравнивались между собой и были использованы для выработки
рекомендаций по устранению расхождений данных и для других ядер.
Основные рекомендации базировались на хорошем (в пределах величины 7
%) согласии данных различных лабораторий для ядра 141Pr.
Данные для сравниваемых сечений (параметры аппроксимирующих
лоренцианов Em,
σm
и Г) приведены
в Таблице 4.
Таблица 4.
Cравнение
[24] результатов экспериментов по определению сечения реакции
141Pr(γ,sn),
выполненных в
разных лабораториях
| Лаборатория | Год | Ссылка | Em, МэВ | σm, мбн | Г, МэВ |
| Ливермор 1 | 1966 | [25] | 15.15 | 324 | 4.42 |
| Джен. Атом. | 1970 | [26] | 15.23 | 341 | 4.00 |
| Саклэ | 1971 | [27] | 15.04 | 347 | 4.49 |
| Иллинойс | 1972 | [11] | 15.36 | 332 | 4.07 *) |
| Ливермор 2 | 1974 | [28, 29] | 15.19 | 344 | 4.24 |
| Ливермор 3 | 1987 | [24] | 15.19 | 340 | 4.15 |
*) Данные, полученные на пучке меченых фотонов.
Выполненное сравнение позволяет сделать некоторые замечания о проявлении определенных систематических расхождений, полезные для анализа их возможных причин:
- сечение, полученное в Саклэ [27] имеет наибольшую величину;
- сачение, определенное в Ливерморе в 1966 году [25], имеет наименьшую величину;
- отношение данных Саклэ [27]/Ливермор [25] составляет 7 %;
- данные, полученные в Ливерморе в трех экспериментах, выполненых, в разные годы (1966, 1974 и 1987) значительно различаются;
- расхождение калибровок (значений Em) трех экспериментов, выполненных в Ливерморе, невелико (40 кэВ), однако все они заметно (170 – 210 кэВ) расходятся с калибровкой экспримента в Саклэ;
заметно различаются и формы (Г) полученных сечений, причем наибольшая ширина ГДР получена в Саклэ.
Относительно хорошее согласие результатов различных экспериментов, полученных для ядра празеодима 141Pr, послужило основанием для выработки рекомендаций по устранению расхождений между данными Ливермора и Саклэ для других ядер, исследованных в работе [24].
Ядро 90Zr. Установлено, что сечение, полученное в Саклэ [30], имеет величину, на 14 % большую, чем сечение Ливермора [24], тогда как для ядра 89Y расхождение данных работ [31] и [24] составляет 22 %, в связи с чем, было рекомендовано все данные работ [30, 31] для ядер 90,91,92,94Zr и 89Y уменьшить на величину 18 ± 4 %.
Ядро 127I. Установлено, что сечение, полученное в Саклэ [32], имеет величину, на 20 % большую, чем сечение Ливермора [24], в связи с чем, рекомендовано ввести для данных Саклэ нормировочный коэффициент 0.8.
Ядро 197Au. На основании аналогичного сравнения данных [24] с сечением, полученным в Саклэ [33], дается рекомендация об использовании для этого последнего нормировочного коэффициента 0.93.
Ядра Pb и Bi. На основании аналогичного сравнения данных [24] с сечениями, полученными в Иллинойсе [11], Ливерморе [34] и Саклэ [33], выработаны рекомендации по увеличению сечений Саклэ на 22 %.
Выработанные рекомендации представлены в Таблице 5.
Таблица 5.
Рекомендованный [24] фактор F (отношение σintЛ/σintС) нормировки данных Саклэ.
-
Ядро Лаборатория Фактор F естRb Саклэ 0.85 ± 0.03 89Sr Саклэ 0.85 ± 0.03 89Y Саклэ 0.82 89Y Ливермор 1.0 90Zr Саклэ 0.88 90Zr Ливермор 1.0 91Zr Ливермор 1.0 92Zr Ливермор 1.0
93Nb Саклэ 0.85 ± 0.03 94Zr Ливермор 1.0 127I Саклэ 0.8 127I Ливермор Рекомендовано не использовать 197Au Саклэ 0.93 197Au Ливермор Рекомендовано не использовать 206Pb Ливермор 1.22 207Pb Ливермор 1.22 208Pb Ливермор 1.22 208Pb Саклэ 0.93 209Bi Ливермор 1.22
Следует
специально отметить, что при анализе расхождений,
которые самими авторами [24] определяются как
«ощутимые (appreciable)», ими в качестве возможных причин
были названы ошибки (погрешности) процедур определения потока фотонов
и эффективности регистрации нейтронов (“…error either in
photon flux determination or in the neutron detection efficiency or
in both”), использованных в Ливерморе. Тем не менее, в качестве
основной рекомендации по устранению обсуждаемых расхождений стала
процедура дополнительной нормировки данных не Ливермора, а Саклэ –
умножения сечений, полученных в Саклэ, на фактор F (Таблица 5).
Данные,
приведенные в Таблице 5, свидетельствуют о том, что предложенные [24]
рекомендации по устранению ощутимых превышений
данных Саклэ над данными Ливермора, двойственны и непоследовательны.
Это вытекает из следующего:
- с одной стороны, абсолютные величины сечений реакций, полученных в Саклэ для всех перечисленных ядер (за исключением ядер 206,207,208Pb и 209Bi), рекомендовалось уменьшить (коэффициенты F = 0.80 0.93), оставляя неизменными (F = 1.0) величины сечений, полученных в Ливерморе – типичные примеры: данные для ядер 89Y и 90Zr;
- с другой стороны, сечения для перечисленных выше ядер 206,207,208Pb и 209Bi, полученные в Ливерморе [25], предлагалось увеличить – домножить на коэффициент 1.22 (выделены в таблице) – с тем, чтобы привести данные для ядра 209Bi в соответствие с данными эксперимента с МФ фотонами [11], выполненного в Иллинойсе (США);
- двойственность и нелогичность использованного подхода становится еще более очевидной, если обратить внимание на то, что данные для ядер 127I [25] и 197Au [35] оказались настолько расходящимися с соответствующими данными Саклэ, что для них никаких количественных рекомендаций выработано не было - вместо этого было рекомендовано эти данные вообще не использовать, как ненадежные.
Определённый разброс от ядра к ядру значений коэффициентов и F делает актуальным задачу системного исследования обсуждаемой ситуации, в общем.
Полная систематика данных по интегральным сечениям .
С целью исследования соотношения абсолютных значений сечений полной фотонейтронной реакции (γ,xn), полученных в разных экспериментах, и выработки последовательных рекомендаций по их приведению в соответствие друг с другом по данным для свыше 500 сечений реакций для ядер от 3H до 238U была получена [16] полная систематика данных для отношениий
| r = Rintсист = σintразные лаборатории(γ,xn)/σintЛивермор(γ,xn) | (4) |
значений интегральных сечений реакций (γ,xn),
полученных в разных лабораториях, к значениям, полученным в одной из
них (конкретно в Ливерморе), представленная на Рис.
4.
Как
и в случае анализа данных по параметру структурности в качестве
своеобразного “эталона” вновь были выбраны данные
Ливермора.
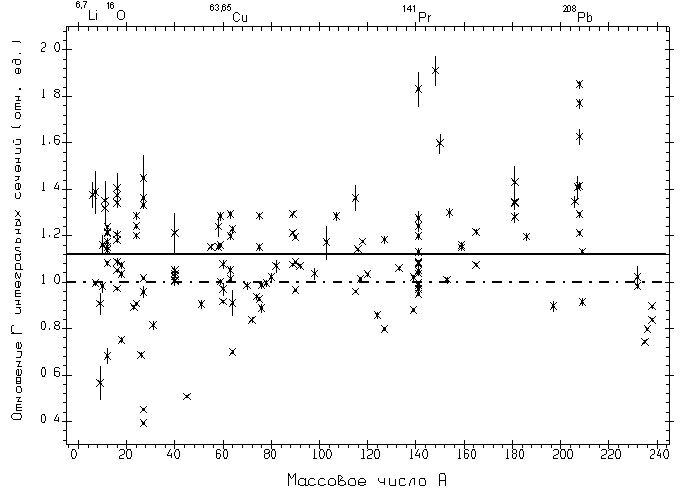 Рис. 4. Систематика [16] значений отношения r = Rintсист = σintразные лаборатории(γ,xn)/σintЛивермор(γ,xn) величин интегральных сечений полной фотонейтронной реакции до порога реакции (γ,2n) для различных ядер, полученных с помощью различных фотонных пучков в разных лабораториях и с помощью квазимоноэнергетических фотонов в Ливерморе. Сплошная линия – среднее значение отношения r = Rintсист. = 1.12, пунктир r = 1.0. |
Для того, чтобы избежать дополнительных
погрешностей, которые могут проявляться при энергиях выше порогов
реакций с различной множественностью фотонейтронов (соотношения
(27) Главы 1), которые будут специально рассмотрены
ниже, значения интегральных сечений для каждого из ядер
рассчитывались для областей энергий между порогами реакций (γ,n)
и (γ,2n)
– фактически приведены интегральные характеристики тех частей
сечений однонейтронных реакций, которые в обеих лабораториях должны
быть идентичными.
Приведенные на Рис.
4 отношения r свидетельствуют о явном расхождении по абсолютной
величине данных Ливермора с данными большинства других лабораторий:
среднее значение отношения <Rintсист> ≠
1, причем подавляющее большинство отношений r располагается в области
значений, больших 1. Несмотря на то, что между данными различных
лабораторий также существуют определенные расхождения, а также на то
обстоятельство, что среди рассчитанных значений отношений r
присутствуют значения, меньшие 1, абсолютное большинство значений
исследуемого отношения отчетливо концентрируются вокруг среднего
значения <r> = <Rintсист> =
1.12.Весьма важно отметить, что КМА данные Саклэ по абсолютной
величине согласуются не с однотипными КМА данными
Ливермора, а с данными, полученными как в КМА экспериментах в
других лабораториях (General Atomic (США), Pennsylvania (США),
Giessen (Германия)), так и в эксперименте с мечеными фотонами
(Illinois (США)), а также и с данными ТИ экспериментов
(выполненными преимущественно в Москве и Мельбурне (Австралия)).
По видимому,
полная систематика данных подтверждает приведенные выше выводы
авторов работы [24] о возможных причинах таких расхождений:
- погрешности в определении эффективности регистрации нейтронов в следствие использования нейтронных детекторов с различными эффективностями (как правило, известными с точностью, не превышающей 10 %)
- неточности процедур определения потока фотонов вследствие исполбзования различных способов определения дозы γ–квантов (точность измерений, например с помощью тонкостенной ионизационной камеры составляет около 10 %);
- отсутствие во многих экспериметах учета самопоглощения фотонов в веществе мишени, что может приводить к погрешностям порядка нескольких %;
- погрешность в определении числа ядер мишеней на участке, обучаемом пучком фотонов, которая может достигать несольких процентов;
- использование различных нормировок при проведении относительных измерений, поскольку сечения реакций-мониторов известны с точностью ~ 5 – 15 %).
Результаты
выполненного анализа требуют по новому взглянуть на рекомендации
работы [24] по проведению согласования данных Ливермора и Саклэ.
Очевидно,
что к их согласованию между собой (а также с данными упоминавшегося
МФ эксперимента [11] и большого количества данных ТИ экспериментов!) приводит не уменьшение (умножение на
коэффициент F (Таблица 5)) данных Саклэ, а напротив –
увеличение данных Ливермора (как это собственно и было сделано в
работе [24] для 206,207,208Pb
и 209Bi).
Естественным образом такое увеличение следует проводить путем
умножения данных Ливермора на коэффициенты 1/F = 1.08
1.25, полученные по данным для коэффициентов F Таблицы 5.
При
таком подходе все значения коэффициентов 1/F оказываются
положительными и близкими к среднему значению приведенной выше
систематики <r> = <Rintсист>
= 1.12. К этому же значению естественно близки и
данные, приведенные в Таблицах 2 и 3, представляющие собой малую
выборку значений полной систематики.
4.1.3. Энергетический центр тяжести сечения реакций
Выше
были отмечены значительные расхождения сечений реакций, полученных в
разных экспериментах, по форме (вследствие, например, различий в
энергетическом разрешении, присутствия переколебаний, перекачки
значений сечения из одной области энергий в другую и т.д.). Были
приведены расхождения, возникающие вследствие различных нормировок
абсолютных величин сечений (асимметричная форма аппаратной функции,
наличие подложек, погрешностей в определении дозы γ–излучения
и эффективности регистрирующей апаратуры).
В дополнение к описанным
выше причинам существенных расхождений результатов разных
экспериментов могут быть указаны и заметные различия энергетических
калибровок разных экспериментов (вследствие, например, различного
определения энергии фотонов, вызывающих реакцию (например, по
максимуму или центру тяжести аннигиляционной линии, различных
способов энергетической калибровки и т.д.).
На Рис. 5
представлена полная систематика [16, 17] данных о значении
параметра ΔEц.т.
| ΔEц.т. = Eц.т. - <Eц.т.>, | (5) |
где Eц.т. =
∫σ(E)EdE/∫σ(E)dE – энергетический центр тяжести
каждого из сравниваемых между собой экспериметальных сечений σ
реакции (γ,xn)
рассчитанный по общей для всех экспериментов области энергий, а
<Eц.т.> - среднее значение
центра тяжести сечения для каждого изотопа.
Из Рис. 5 видно, что
энергетические центры тяжести сечений реакции, полученных в разных
экспериментах, как правило, не совпадают друг с другом. Они
оказываются сдвинутыми друг относительно друга на энергию, в среднем
имеющую величину <Eц.т.> ~
200 кэВ (в отдельных случаях – до 400 кэВ), стандартное
отклонение составляет ± 83.6
кэВ: при сравнении или совместной обработке сечений реакций из разных
экспериментов, для достижения наилучшего согласия допустимо сдвигать
их навстречу друг-другу по энергии на величину ~ 160 кэВ (или одного
к другому на величину ~ 300 кэВ).
В
качестве возможных причин возникновения погрешностей калибровки
энергетической шкалы сечений в разных экспериментах, вызывающих
смещения друг относительно друга энергетических центров тяжести
сечений реакций (5), могут быть названы следующие:
- различные методы калибровки по энергии ТИ-пучков (калибровка по известным порогам или изломам в кривых выхода реакций приводит к точностям энергетической шкалы порядка 100 —200 кэВ);
- систематические различия в определении энергетической шкалы при решении обратной задачи определения сечения реакции по экспериментальному выходу в ТИ-экспериментах различными методами и с различным шагом обработки (точность при этом составляет половину шага обработки);
- систематические расхождения в определении энергетической шкалы в разных КМИ-экспериментах (например, по энергии позитронов или центру тяжести эффективного спектра фотонов ) достигают 200 —400 кэВ и т.д.
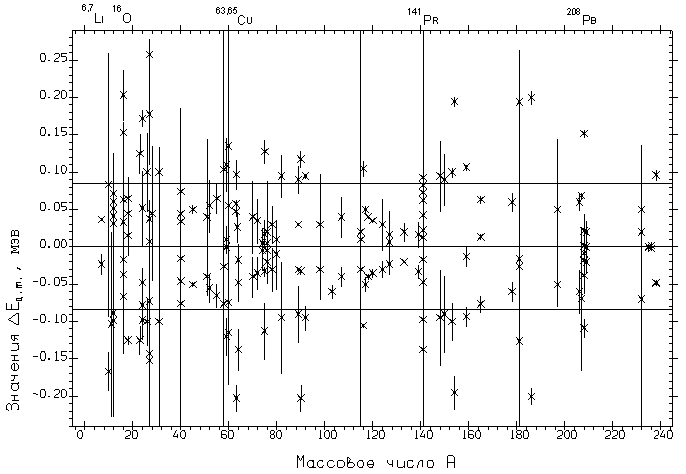 Рис. 5. Систематика данных о величине отклонений энергетического центра тяжести Eц.т. сечения полной фотонейтронной реакции от среднего значения для различных ядер. Пунктирные линии - границы области стандартного отклонения. |
Приведенные данные свидетельствуют о том, что в энергетических калибровках экспериментов имеются систематические погрешности, которые при совместном анализе, оценке, использовани в комбинациях исходных сечений должны учитьываться путем внесения соответсвующих поправок. Эти поправки должны сближать однозначно идентифицированные особенности сечений, таким образом, чтобы не происходило заметного (превышающего величину ~ 2 x 83.6 = 167.2 кэВ) смещения центров тяжести корректируемых сечений.
4.2. Расхождения сечений парциальных фотонейтронных реакций (γ,n) и (γ,2n), полученных в КМА экспериментах в Ливерморе (США) и Саклэ (Франция)
Выше
были проанализированы расхождения величин интегральных сечений полной
фотонейтронной реакции (γ,xn)
(соотношение (27а) Главы 1), полученных в различных экспериментах.
Было установлено, что данные Ливермора систематически отличаются по
абсолютной величине от
данных других лабораторий, и показано, что
согласование данных может быть достигнуто путем дополнительной
нормировки данных Ливермора.
Наряду
с расхождениями сечений полной фотонейтронной реакции, определяемой в
экспериментах непосредственно, ещё более серьезные расхождения были
обнаружены для сечений составляющих её парциальных реакций –
(γ,n)
и (γ,2n)
– для определения множественности которых используются
специальные методы, описанные в Главе 1. Выше
упоминалось, что значительные расхождения данных Ливермора и Саклэ по
сечениям реакций (γ,n)
и (γ,2n)
были установлены [22, 23] при их совместном анализе для 12 ядер –
89Y, 115In,
117,118,120,124Sn,
133Cs, 159Tb,
165Ho,
181Ta, 197Au,
208Pb (Таблица
3).
К
сожалению, в работах [22, 23] сравнение абсолютных величин сечений
реакций проводилось на основании данных не об их интегальных
характеристиках, а об амплитудах ГДР, корректировка
энергетических шкал проводилась по областям энергий, в которых уже
проявляются недостатки процедуры определения множественности
фотонейтронов, а к тому же некоторые данные были использованы
ошибочно. В этой связи, полученные [22, 23] данные были
затем в значительной степени пересмотрены и уточнены [36]. Кроме того
были получены [36] аналогичные данные ещё для 7 ядер – 51V,
75As, 90Zr,
116Sn,
127I,
232Th,
238U.
В
Таблице 6 приведены скорректированные значения отношений
(Саклэ/Ливермор) раздельно для интегральных
сечений полной (Rint(xn)
= σintС(γ,xn)/σintЛ(γ,xn))
и парциальных
(Rint(n)
= σintС(γ,n)/σintЛ(γ,n)
и Rint(2n) =
σintС(γ,2n)/σintЛ(γ,2n))
фотонейтронных реакций, полученные в совпадающих областях энергий для
всех 19 рассмотренных ядер.
Из
данных Таблицы 6 ясно видно, что, как уже отмечалось выше, в то время
как величины интегральных сечений полной фотонейтронной реакции
(γ,xn),
полученные в Саклэ, превышают величины, полученные в Ливерморе, на 6
– 15 %
(в соответствии с данными полной систематики (Рис. 3 и Таблицы 3, 6),
величины интегральных сечений парциальных реакций соотносятся между
собой существенно иначе. В то время как для реакции (γ,n)
данные Саклэ также заметно превышают данные Ливермора, для реакции
(γ,2n)
наблюдается обратное соотношение.
Таблица 6.
Сравнение [36] величин отношений (Саклэ/Ливермор) интегральных сечений реакций (γ,n), (γ,2n) и (γ,хn) – соответственно Rint(n), Rint(2n) и Rint(xn).
| Ядро | Rint(n) *) | Rint(2n) | Rint(xn) *) |
| 51V | 1.07 | 0.79 | 1.07 |
| 75As | 1.21 | 1.22 | 1.21 |
| 89Y | 1.25 | 0.87 | 1.25 |
| 90Zr | 1.26 | 0.73 | 1.26 |
| 115In | 0.97 | 0.76 | 0.97 |
| 116Sn | 1.10 | 0.92 | 1.10 |
| 117Sn | 1.02 |
0.93 |
1.02 |
| 118Sn | 1.07 | 0.86 | 1.07 |
| 120Sn | 1.00 | 0.86 | 1.00 |
| 124Sn | 0.93 | 0.94 | 0.93 |
| 127I | 1.34 | 1.07 | 1.34 |
| 133Cs | 1.10 | 0.88 | 1.10 |
| 159Tb | 1.07 | 0.71 | 1.07 |
| 165Ho | 1.20 | 1.05 | 1.20 |
| 181Ta | 1.25 | 0.89 | |
| 197Au | 1.00 | 0.69 | 1.00 |
| 208Pb | 1.21 | 0.77 | 1.21 |
| 232Th | 0.84 | 0.69 | 0.84 |
| 238U | 0.76 | 0.79 | 0.76 |
*) До порога реакции (γ,2n) отношения практически совпадают (отличия – в третьем знаке).
Реакции
(γ,n)
и (γ,2n)
оказываются связанными (соотношение (20) Главы 1), вследствие чего
определение сечения одной из них с большой систематической
погрешностью неизбежно приводит к значительной систематической
погрешности в сечении другой реакции. Очевидно также, что занижение
абсолютного значения сечения реакции (γ,n)
приводит к завышению абсолютного значения сечения реакции (γ,2n)
и, соответственно, наоборот.
Полная
систематика обсуждаемых отношений интегральных сечений парциальных
фотонейтронных реакций для 19 перечисленных выше ядер представлена на
Рис. 6.
Отмеченные
выше расхождения интегральных сечений реакций проявляются отчетливо
для 14 из 19 исследованных ядер: если сечения реакции (γ,n),
полученные в Саклэ, имеют большие величины, чем в Ливерморе (квадраты
в основном расположены в области значений, больших 1.0), то для
сечений реакции (γ,2n)
соотношение оказывается обратным (треугольники в основном расположены
в области значений, меньших 1.0).
Исключения
составляют данные для 5 ядер 75As,
127I, 165Ho,
124Sn и 238U.
Отношения для первых трех из них названы «Особые случаи»,
поскольку для них треугольники (отношения для реакций (γ,2n))
располагаются в области выше 1.0. Отношения для двух последних –
«Идеальные случаи» – условно названы так потому,
что для них треугольники и квадраты оказываются близкими и друг к
другу.
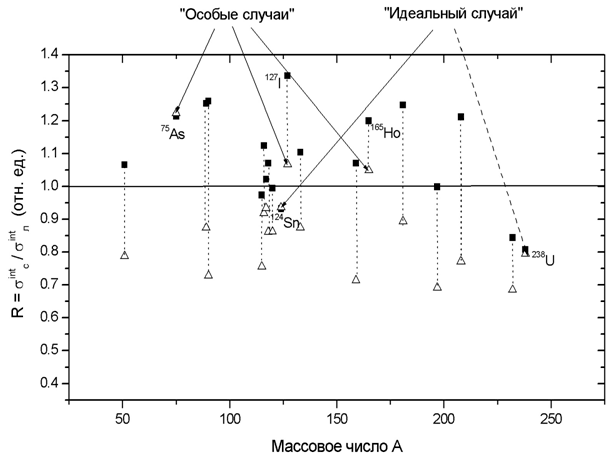 Рис. 6. Систематика значений (Таблица 6) отношений R(n) = σintСаклэ(γ,n)/σintЛивермор(γ,n) – квадраты и R(2n) = σintСаклэ(γ,2n)/σintЛивермор(γ,2n) – треугольники, полученных после соответствующей корректировки энергетических шкал для согласованных диапазонов интегрирования по данным экспериментов, выполненных в Саклэ и Ливерморе. |
В работе [36] показано, что появление «особых» и «идеальных» случаев обусловлено тем, что, в отличие от остальных 14 ядер, для перечисленных 5 ядер значения Rинт(xn) = σинтС(γ,xn)/σинтЛ(γ,xn) ≠ const и зависят от энергии фотонов Eγ в областях энергий выше порогов реакции (γ,2n). Это свидетельствует о наличии дополнительных погрешностей, которые должны учитываться специальным образом. Учёт таких погрешностей был сделан в работе [36] с помощью введения вместо постоянных отношений Rint(xn) соответствующих функций энергии фотонов R(Eγ).
4.3. Влияние систематических погрешностей результатов отдельных экспериментов на взаимную обработку нескольких из них
Для
повышения точности данных о сечениях полного фотопоглощения и каналах
распада ГДР, необходимых для проведения на современном уровне
детальных исследований многих особенностей фоторасщепления атомных
ядер, использования данных в разнообразных приложениях, требуется
объединение информации возможно максимального числа независимых
измерений. Однако в условиях, когда результаты отдельных
экспериментов существенно расходятся друг с другом, и простое
сравнение, а тем более комбинирование данных из разных экспериментов
представляет собой во многих случаях нетривиальную задачу. Эта задача
требует для своего решения возможно более полного учета всех
проявляющихся систематических расхождений (аппаратная функция,
абсолютная нормировка, энергетическая калибровка) и связанных с ними
погрешностей экспериментов.
Приведенные выше данные
свидетельствуют о том, что в то время, как в каждом из
экспериментальных сечении достигнута достаточно высокая (~ 5 –
10 %) статистическая точность, систематические расхождения между
отдельными сечениями намного превосходят статистический разброс точек
каждого из них и составляют около 30 – 35 %. В таких условиях
оценка точности каждого отдельного сечения лишь по его статистической
погрешности представляется неправомочной: необходимо оперировать
полной погрешностью
| Δσполн. = Δσстатист. + Δσсистемат.. |
(6) |
В связи со
всем сказанным, очевидно, что простое объединение (суммирование или
объединение с весами) соответствующих значений всех сечений без учета
систематических погрешностей может привести к существенной петере
информации. Безусловно, такое объединение естественным образом
уменьшит значение Δσстатист.
(повысит статистическую точность до значений ~ 1.5 – 2.0 %!),
но никак не изменит величину систематической погрешности, которая так
и останется равной ~ 30 - 35 %. Поскольку расхождения между
отдельными сечениями могут иметь разную природу – погрешности в
нормирове и энергетической калибровке, одним из следствий такого не
вполне корректного объединения станет существенная потеря информации:
усредненные или средневзвешенные сечения окажутся существенно более
гладкими по сравнению с исходными. Из приведенных ранее данных ясно,
форма сечения, полученного их простым объединением, может существенно
измениться. Так, например, в наличие в объединенном сечении всего
лишь одного отчетливо выраженного максимума в то время, как каждое из
объединяемых содержит их, к примеру, два, представляет собой именно
искажение (потерю) информации о сечении.
Природу
влияния систематических погрешностей обсуждаемого типа на результат
объединения результатов нескольких экспериментов иллюстрирует Рис. 7,
на котором приведены очень простые, наглядные и очевидные примеры
получения суммы и разностой двух сечений, каждое из которых имеет
форму единственного резонанса и получено при одинаковых идеальных
(гаусианоподобных) аппаратных функциях.
На
Рис. 7 в верхней части показывается, каким образом получаются сумма и
разности рассматриваемых сечений в идеальных условиях. Если для
расматриваемых двух сечений имеется всего лишь небольшое расхождение
калибровок (сдвиг энергетических шкал сравниваемых сечений
относительно друг друга), то сумма исходных сечений (Рис. 7,
середина) уже не будет соответствовать исходным аппаратным функциям.
Она будет представлять собой искаженное и к тому же уширенное сечение
(в определенном смысле), то есть имеющее худшее энергетическое
разрешение. Такое получение информации о суммарном сечении при
искаженной аппаратной функции означает искажение (потерю) информации
о самом сечении.
Еще
более существенным окажется потеря информации о сечении, которое
будет представлять собой результат вычитания одного из них их
другого.
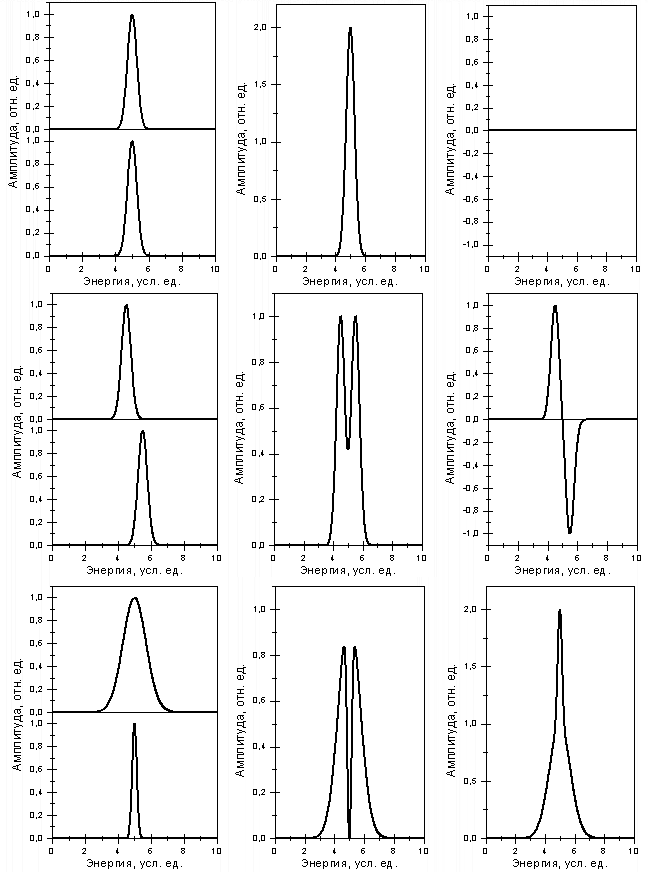 Рис. 7. Влияние расхождений в аппаратных функциях двух экспериментов (столбцы слева) на структуру сечения реакции, получаемого в результате суммирования их результатов (столбцы посередине) и вычитания одного из другого (столбцы справа): сверху – при сопадении калибровок и разрешений; посредине – при расхождении калибровок; внизу – при расхождении разрешений. |
На Рис. 7
(внизу) видно, что без специальной корректировки энергетических шкал
полученный таким образом результат – разность сечений –
по существу уже вообще не будет сечением, поскольку соответственно
форме результирующей аппаратной функции – разности аппаратных
функций,
при которых были получены уменьшаемое и вычитаемое сечения -
будет содержать области отрицательных значений.
Такое
«сечение», имеющее отрицательные значения в областях
отрицательных значений результирующей апаратной функции, будет по
существу представлять нефизический результат.
Рис.
7в иллюстрирует искажения информации о сечении, которые возникают в
том случае, когда данные получены при одной и той же калибровке, но
при различных энергетических разрешениях.
Следует обратить
особое внимание на то обстоятельство, что пренебрежение
систематическими погрешностями сравниваемых сечений реакций будет
вести к тем большим искажениям в результирующем сечении, чем с
большей статистической точностью получены сечения исходныеТак,
например, чем с более высоким энергетическим разрешением будут
получены исходные сечения, тем меньшие рассогласования их
энергетических шкал будут приводить к потере информации об этих
сечениях в результате их совместной обработки. Так, суммирование
сечений, определенных с высоким разрешением, при достаточно больших
расхождениях калибровок будет приводить к тому, что, например, вместо
одного максимума появятся два, то есть в суммарном сечении будет
получена ложная (отсутствующая в исходных сечениях) структура. В то
же время, в сечении, полученном, как разность других, напротив,
искажения будут заключаться в том, что реальные максимумы, попадая в
область отрицательных значений результирующей аппаратной функции,
будут ослабляться или вообше исчезать.
Таким
образом, совместная обработка результатов разных экспериментов без
достаточно детального анализа присутствующих в них систематических
погрешностей будет приводить к искажениям не только абсолютных
величин результирующих сечений, но и их формы. Простой пример того,
как к подобным искажениям величины и формы исследуемого сечения
реакции приводит проведение простейшей разностной процедуры без учета
обсуждаемых систематических погрешностей, представлен на Рис. 8 [37].
Сечение
реакции 63Сu(γ,np)61Ni
определялось из анализа разности двух экспериментальных сечений с
применением соотношения
| σ(γ,np) = σ[(γ,n) + (γ,np)] - σ(γ,n) | (7) |
к
результатам двух экспериментов. В одном из них [27] сечение реакции
63Cu(γ,n)62Cu
было определено с помощью метода наведенной активности, в другом
[38] сечение реакции 63Cu[(γ,n)
+ (γ,np)]
было получено с помощью прямой регистрации фотонейтронов и их
разделения по множественности. Оба экспериментальных сечения
приведены на Рис. 8а.
Представленные
данные свидетельствуют о присутствии систематических погрешностей,
которые кратко обсуждались выше – сумма сечений реакций (γ,n)
и (γ,np)
имеет меньшую абсолютную величину, чем сечение реакции (γ,n).
Очевидно, что присутствуют погрешности, как нормировки, так и
энергетической калибровки сечений обоих (или одного из них, по
крайней мере – рассогласования этих параметров в обоих
экспериментах).
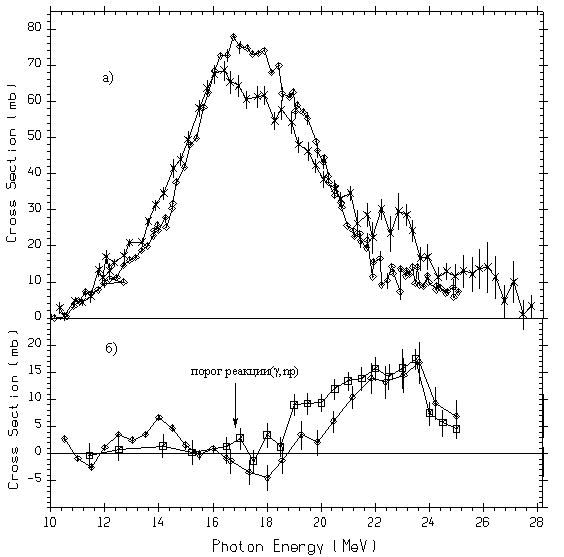 Рис. 8. Сравнение сечений реакции 63Cu(γ,np)61Ni, оцененных разными способами: а – сечения реакций 63Cu(γ,n)62Cu (ромбы, [37]) и 63Cu[(γ,n)+(γ,np)] (кресты, [38]); б – сечение реакции 63Cu(γ,np)61Ni: ромбы - данные [37] о сечении реакции (γ,np), полученные с использованием простой нормировки данных о сечениях реакций [(γ,n)+(γ,np)] и (γ,n); квадраты - данные [39] о сечении реакции (γ,np), полученные с помощью совместной обработки данных о сечениях реакций [(γ,n)+(γ,np)] и (γ,n) с помощью метода редукции. |
Для
устранения систематических расхождений была выполнена [37] простая
нормировка данных обоих экспериментов в области энергий ниже порога
реакции 63Cu(γ,np)61Ni
(Eпор. = 16.7 МэВ), а конкретно – при Eγ
= 160 МэВ (на Рис. 8а хорошо видно совпадение при этой энергии
абсолютных значений обоих сечений).
Полученное
с применением после этого соотношения (7) сечение 63Cu(γ,np)61Ni
приведено на Рис. 8б (ромбы) и характеризуется наличием областей, в
которых сечение представляет собой нефизический результат:
- большие положительные значения (до 10 мбн) при энергиях 12 – 16 МэВ (ниже порога Eпор. = 16.7 МэВ);
- большие отрицательные значения при энергиях выше порога (до -4,5 мбн при Еγ = 18 МэВ).
Происхождение
областей с отрицательными значениями напрямую связано с эффектами,
которые проиллюстрированы на Рис. 7б – на Рис. 8а хорошо видны
различия и по величине и по форме обоих сечений. Наличие нефизических
областей в сечении 63Cu(γ,np)61Ni
[28] в соответствии со сказанным выше указывает на ненадежность
(недостаточность) использованной процедуры взаимной нормировки
сечений из работ [37] и [38], выполненной без учета отмечавшихся
погрешностей энергетических калибровок обоих экспериментов.
На
Рис. 8б приведено сечение (квадраты), оцененное нами [39] с помощью
метода редукции (см. далее Главу 5) при учете имеющихся
систематических расхождений обрабатываемых данных и по абсолютным
величинам и по калибровке энергетических шкал.
Для этого предварительно
сечение реакции 63Cu(γ,n)62Cu
было оценено (Рис. 9) с помощью метода редукции на основе результатов
9 различных экспериментов (в том числе и сечения реакции, полученного
в работе [37]).
Как отмечалось ранее в Главе
1 (см. далее Главу 5), метод редукции позволяет преобразовать каждое
сечение, полученное со своей формой аппаратной функции и при своей
калибровке, к виду, которое оно имело бы, будучи полученным при
некоторой другой - единой для всех эксперирментов аппаратной функции.
При формировании такой
единой аппаратной функции (формулировании требований к ней) может
учитываться и различие калибровок каждого эксперимента, например, на
основании приведения в соответствие таких обобщенных характеристик
каждого из сечений, значения центров тяжести и интегральных сечений.
Учет систематических расхождений при переходе к единой аппаратной
функции позволяет получить более правильные величину и форму
оцененного сечения, а объединение информации нескольких сечений при
учете систематических погрешностей каждого позволяет в оцененном
сечении достигнуть большей статистической точности.
Конкретное
сравнение (Рис. 9) оцененного сечения реакции (сплошная линия) с
обсуждавшимся выше сечением [37] (квадраты) показывает, к каким
именно изменениям приводит учет упомянутых систематических
погрешностей:
- оцененное сечение имеет максимум, сдвинутый в сторону меньших энергий на величину ~400 кэВ (16.54 вместо 16.97 МэВ);
- оцененное сечение имеет несколько иную форму, прежде всего на начальном участке до энергий ~ 19 МэВ.
 Рис. 9. Экспериментальные сечения, полученные в 9 различных экспериментах и оцененное с помощью метода редукции (сплошная линия) сечения фотонейтронной реакции 63Cu(γ,n)62Cu. |
Новые надежные параметры взаимной нормировки и
калибровки оцененного сечения реакции 63Cu(γ,n)62Cu
[39] с сечением реакции 63Cu[(γ,n)+(γ,np)]
[28], основанные на данных о центрах тяжести и интегральных сечениях
(а не на абсолютных величинах сравниваемых сечений в одной точке при)
позволили применить ту же разностную процедуру (7), однако в условиях
учета взаимных систематических расхождений.
Сравнение
приведенных на Рис. 8б данных, полученных с учетом систематических
погрешностей и без него, наглядно иллюстрирует все сказанное выше о
влиянии рассогласований аппаратных функций экспериментов на конечный
результат их взаимной обработки (в данном случае вычитания одного
результата из другого). В оцененном сечении реакции (γ,np)
также имеется
отрицательный резонанс на начальном участке сечения (~ 12 – 15
МэВ), обусловленный тем обстоятельством, что кроме систематических
погрешностей обсуждаемых типов, в результатах одного (или
обоих)
экспериментов, имеются и определенные неучтенные погрешности иного
типа, о чем свидетельствует некоторое (незначительное) расхождение
обрабатываемых сечений по форме.
Из
данных Рис. 8б видно, каким образом корректировка обоих сечений с
помощью метода редукции позволяет устранить их основные
систематические расхождения – амплитуда наблюдающегося в
оцененном сечении отрицательного резонанса находится практически в
пределах статистических погрешностей (интегральное сечение на этом
участке равно 1.4 ±
1.3 МэВ·мбн,
тогда как в сечении, полученном в работе [37], оно имело заметно
большую величину - 5.9 ±
2.7 МэВ·мбн).
Следует
особо отметить, что даже в простейшем рассмотренном случае в полном
соответствии со сказанным выше отсутствие учета систематических
погрешностей энергетических калибровок двух совместно обрабатываемых
сечений реакций привело [37] к искажению не только абсолютной
величины результата такой обработки, но и наблюдаемой в нем
промежуточной структуры. Точность оцененного с помощью метода
редукции сечения [39] позволяет надежно интерпретировать лишь один
максимум при энергии 23.6 МэВ и некотрую относительно слабую
особенности при энергии 22.0 МэВ. В то же время в полученном ранее
сечении реакции [37] на уровне достигнутой статистической точности
как достаточно «надежно» выделенные обсуждались 7
максимумов при энергиях 12.3, 14.0, 17.0, 18.0, 19.1, 22.0 и 23.6
МэВ.
Очевидно,
что в более сложных случаях такие искажения структурных особенностей
сечений также будут присутствовать, однако не будут столь явными, как
в рассмотренном простейшем случае. Рассогласования энергетических
калибровок могут приводить как к возникновению ложной структуры, так
и к заглаживанию реальной структуры.
Систематические расхождения
результатов разных экспериментов должны учитываться также и при
определении информации о сечениях одних реакциям по сечениям других,
что широко используется в тех случаях, когда искомые сечения могут
быть определены не прямо, а лишь в каких то комбинациях с другими.
При отсутствии учета
систематических расхождений информация о сечениях реакций, получаемая
в фотоядерных исследованиях с помощью упомянутой выше комбинации (7),
а также ряда других широко используемых, например,
| σ(γ,р) = σ[(γ,р) + (γ,np)] – σ(γ,np), | (8а) |
| σ(γ,2n) ≈ 1/2[σ(γ,xn) – σ(γ,n) – σ(γ,np)], | 8б) |
| σ(γ,sn) ≈ σ(γ,abs) - σ (γ,p), | (8в) |
так же, может быть в значительной степени
искажена – искажение абсолютной величины, появление ложной или
заглаживание реальной структуры, появление нефизических областей.
Очевидно, что для
предотвращения (или, по крайней мере, снижения влияния)
систематических расхождений обсуждаемого типа на характеристики
определяемых сечений реакций, при обработке данных разных
экспериментов должны быть приняты
специальные меры – их нормировки и
калибровки должны быть унифицированы, аппаратные функции максимально
приближены друг к другу [40 – 48].
- E.G.Fuller, H.Gerstenberg. Photonuclear Data - Abstracts Sheets 1955 - 1982. NBSIR 83-2742. U.S.A. National Bureau of Standards, 1983.
- В.В.Варламов, В.В.Сапуненко, М.Е.Степанов. Фотоядерные данные 1976 - 1995. Указатель. Издательство Московского университета, -M., 1996.
- S.S.Dietrich, B.L.Berman. Atomic Data and Nuclear Data Tables, 38 (1988) 199. B.L.Berman, S.C.Fultz. Rev.Mod.Phys., 47 (1975) 713.
- A.V.Varlamov, V.V.Varlamov, D.S.Rudenko, M.E.Stepanov. Atlas of Giant Dipole Resonances. Parameters and Graphs of Photonuclear Reaction Cross Sections. INDC(NDS)-394, IAEA NDS, Vienna, Austria, 1999.
- Б.С.Ишханов, И.М.Капитонов, Е.В.Лазутин, И.М.Пискарёв, В.С.Сопов, В.Г.Шевченко. Ядерная физика, 12 (1970) 892.
- A.Veyssiere, H.Beil, R.Bergere, P.Carlos, A.Lepretre, A.De Miniac. Nucl.Phys., A227 (1974) 513.
- R.L.Bramblett,
J.T.Caldwell,
R.R.Harvey,
S.C.Fultz.
Phys.Rev., 133 (1964) B869.
J.T.Caldwell, R.L.Bramblett, B.L.Berman, R.R.Harvey. Phys.Rev.Lett., 15 (1965) 976. - R.E.Pywell, M.N.Thompson, B.L.Berman. Nucl.Instr. and Meth., 178 (1980) 149.
- J.G.Woodworth, K.G.McNeill, J.W.Jury, R.A.Alvarez, B.L.Berman, D.D.Faul, P.Meyer. Phys.Rev., C19 (1979) 1667.
- В.В.Варламов, Н.Г.Ефимкин, Б.С.Ишханов, В.В.Сапуненко. Вопросы атомной науки и техники. Серия: Ядерные константы, 1 (1993) 52.
- L.M.Young. Photoneutron Cross Sections and Spectra from Monoenergetic Photons on Yttrium, Praseodimium, Lead, and Bismuth in the Giant Resonance. Ph.D. Thesis, University of Illinois, USA, 1972.
- L.S.Cardman. Photon Tagging. Present Practice and Future Prospects. Preprint P/83/12/168, University of Illinois at Urbana -Champaign, 1983.
- В.В.Варламов, Б.С.Ишханов, Ю.П.Пытьев, А.П.Черняев, Д.В.Юдин. Вестник Московского университета. Физика, Астрономия. 25 (1984) 53.
- В.В.Варламов, Б.С.Ишханов, Н.Г.Ефимкин, А.П.Черняев. Известия АН СССР, серия физическая, 55, 1021 (1991).
- N.G.Efimkin, B.S.Ishkhanov, Ju.P.Pyt'ev, V.V.Varlamov. The Energy Resolution Improvement by the Method of Reduction in Photonuclear Experiments. MSU INP Preprint-91-35/239, -M., 1991.
- В.В.Варламов, Б.С.Ишханов, Д.С.Руденко, М.Е.Степанов. Ядерная физика, 67 (2004) 2131.
- N.G.Efimkin, V.V.Varlamov. The Method of Reduction as Photonuclear Data Evaluation Tool. International Symposium on Nuclear Data Evaluation Methodology (USA BNL, 12 - 16 October 1992). World Scientific Press, ISBN 981-02-1285-2, 1993, p. 585.
- В.В.Варламов, Б.С.Ишханов, М.Е.Степанов. Известия РАН, серия физическая, 62 (1998) 1035.
- В.В.Варламов, Д.С.Руденко, М.Е.Степанов. Оценка сечения реакции 34S(γ,sn) с помощью метода редукции. Тезисы докладов Международной конференции по ядерной физике “Кластеры в ядерной физике”. L Совещание по ядерной спектроскопии и структуре ядра. Санкт-Петербург, 14 - 17 июня 2000 г., -С -Пб, 2000, с. 349.
- Ю.П.Пытьев. Методы анализа и интерпретации эксперимента. Издательство Московского университета, -М, 1990.
- Ю.П.Пытьев. Методы математического моделирования измерительно-вычислительных систем. Физматлит. -М, 2002.
- B.L.Berman, R.E.Pywell, S.S.Dietrich, M.N.Thompson, K.G.McNeill, J.W.Jury. Phys.Rev., C36 (1987) 1286.
- R.L.Bramblett, J.T.Caldwell, B.L.Berman, R.R.Harvey, S.C.Fultz. Phys.Rev., 148 (1966) 1198.
- R.E.Sund, V.V.Verbinski, H.Weber, L.A.Kull. Phys.Rev., C 2 (1970) 1129.
- H.Beil, R.Bergere, P.Carlos, A.Lepretre, A.Veyssiere, A.Parlag. Nucl.Phys., A172 (1971) 426.
- J.T.Caldwell, E.J.Dowdy, B.L.Berman, R.A.Alvarez, P.Meyer. Phys.Rev., C 21 (1980) 1215.
- B.L.Berman, J.T.Caldwell, E.J.Dowdy, S.S.Dietrich, P.Meyer. Phys.Rev., C 34 (1986) 2201.
- A.Lepretre, H.Beil, R.Bergere, P.Carlos, A.Veyssiere, M.Sugawara. Nucl.Phys., A 175 (1971) 609.
- B.L.Berman, J.T.Caldwell, R.R.Harvey, M.A.Kelly, R.L.Bramblett, S.C.Fultz. Phys.Rev., 162 (1967) 1098.
- R.Bergere, H.Beil, P.Carlos, A.Veyssiere. Nucl.Phys., A 133 (1969) 417.
- A.Veyssiere, H.Beil, R.Bergere, P.Carlos, A.Lepretre. Nucl.Phys., A 159 (1970) 561.
- R.R.Harvey, J.T.Caldwell, R.R.Bramblett, S.C.Fultz. Phys.Rev., B136 (1964) 126.
- S.C.Fultz, S.C.Fultz, J.T.Caldwell, N.A.Kerr. Phys.Rev., 127 (1962) 1273.
- E.Wolynec, A.R.V.Martinez, P.Gouffon, Y.Miyao, V.A.Serrao, M.N.Martins. Phys.Rev., C29 (1984) 1137.
- E.Wolynec, M.N.Martins. Revista Brasileira Fisica, 17 (1987) 56.
- В.В.Варламов, Песков Н.Н., Руденко Д.С., Степанов М.Е. Вопросы атомной науки и техники. Сер. «Ядерные константы», 1- 2 (2003) 48.
- R.E.Sund, M.P.Baker, L.A.Kull, R.B.Walton. Phys.Rev., 176 (1968) 1366.
- В C.Fultz, R.L.Bramblett, J.T.Caldwell, R.R.Marvey. Phys.Rev., B133 (1964) 1149.
- В.В.Варламов, Н.Г.Ефимкин, Б.С.Ишханов, В.В.Сапуненко, М.Е.Степанов. Ядерная физика, 58 (1995) 387.
- V.V.Varlamov, N.N.Peskov. Evaluation of (γ,xn), (γ,sn), (γ,n), (γ,2n), and (γ,f) Reactions Cross Sections for Actinides Nuclei 232Th, 238U, 237Np, and 239Pu: Consistency Between Data Obtained Using Quasimonoenergetic Annihilation and Bremsstrahlung Photons. Preprint MSU SINP 2007-8/829.
- В.В.Варламов, Д.С.Руденко, М.Е.Степанов. Вестник Московского университета. Серия 3. Физика. Астрономия. № 6 (2004) 19.
- В.В.Варламов, Б.С.Ишханов, Д.С.Руденко, М.Е.Степанов. Ядерная физика, 67, №12 (2004) 2131.
- B.S.Ishkhanov, V.V.Varlamov. Photonuclear Reactions: Modern Status of the Data. Ядерная физика, 67, No 9 (2004) 1691.
- В.В.Варламов, Б.С.Ишханов. Физика элементарных частиц и атомного ядра, том 35, вып. 4, 2004, с. 858.
- В.В.Варламов, М.Е.Степанов. Ядерная физика, 65, N1 (2002) 1.
- V.V.Varlamov, B.S.Ishkhanov. Study of Consistency Between (γ,xn), [(γ,n) + (γ,np)] and (γ,2n) Reaction Cross Sections Using Data Systematics. Vienna, Austria. INDC(CCP)-433, IAEA NDS, Vienna, Austria, 2002.
- В.В.Варламов, Н.Г.Ефимкин, Б.С.Ишханов, В.В.Сапуненко, М.Е.Степанов. Ядерная физика, 58 (1995) 387.
- В.В.Варламов, Б.С.Ишханов, В.В.Сургутанов, А.П.Черняев, Р.А.Эрамжян. Известия АН СССР, серия физическая, 51 (1987) 195.