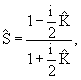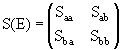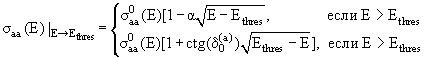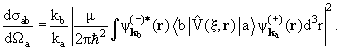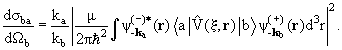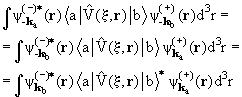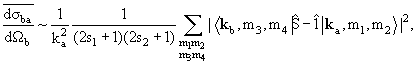Раздел III Вопросы симметрии, унитарности и аналитичности

Лекция 16. Унитарность S-матрицы. Дисперсионные соотношения. Связь сечений прямых и обратных процессов

§ 16.1. Унитарность S-матрицы и ее следствия

    Много важных закономерностей столкновительных процессов можно установить, не задавая ни конкретных свойств взаимодействий, ответственных за столкновение, ни конкретных особенностей структуры сталкивающихся объектов. Закономерности такого рода являются следствием самых общих законов природы, например законов сохранения и тесно связанных с ними общих требований симметрии. Как при рассмотрении вопросов структуры стабильных квантовых систем (см., например, [1, § 57-58]), так и в квантовой теории столкновений симметрийный и динамический подходы применяются обычно в тесной связи между собой, дополняя и усиливая возможности друг друга.
    Унитарность S-матрицы (Ŝ-оператора):

является важнейшим общим требованием последовательной квантовой теории. В лекции 7 мы доказали это соотношение для случая рассеяния частицы на заданном потенциале. Обобщим его на многоканальный случай.
    Пусть ψ_in − волновая функция начального (входного) состояния рассматриваемой физической системы, которая состоит из двух подсистем, не взаимодействующих друг с другом на больших относительных расстояниях. Ŝ-оператор переводит ее в волновую функцию выходного состояния:

и, подобно (7.32), выражается через мёллеровские операторы ₋ и ₊, которые в свою очередь связаны предельным соотношением (7.30) с полным гамильтонианом Ĥ = Ĥ₀ + и с гамильтонианом невзаимодействующих подсистем Ĥ₀.
    Пусть векторы |а > образуют некоторый полный набор состояний невзаимодействующих подсистем. Тогда, очевидно, матричный элемент < b|Ŝ|a > есть амплитуда вероятности того, что рассматриваемая физическая система, находившаяся при t → ∞ в состоянии |а >, окажется в результате процесса столкновения в состоянии |b > , а величина

это вероятность такого процесса. Записывая соотношение унитарности (16.1) в явном матричном виде:

получаем отсюда при а = а'

т.е.

Таким образом, физический смысл требования унитарности − это нормировка на 100% суммарной вероятности того, что в процессе столкновения система окажется в одном из состояний полного набора |b >.
    При b ≠ а величина Р_bа = |< b|Ŝ|a >|² есть вероятность перехода |а > → |b >. Если же взаимодействие между подсистемами отсутствует, то, согласно (16.2), Ŝ-оператор сводится к единичному оператору:

Ŝ =

(16.7)

Поэтому для описания эффекта упругого рассеяния |а > → |a > надо использовать оператор Ŝ − и, следовательно, вероятность упругого рассеяния дается формулой

Paa = |< a|Ŝ − |а >|2.

(16.8)

Ввиду ортогональности состояний полного набора <b|а> = δ_аb формулу (16.8) можно записать и в общем случае:

Pba = |< b|Ŝ − |а >|2.

(16.9)

    Далее рассмотрим, для простоты, столкновение бесспиновых частиц. В этом случае орбитальный момент ℓ относительного движения сталкивающихся частиц сохраняется, и полное сечение столкновения есть сумма полных сечений столкновения для частиц с разными ℓ. Так, в задаче потенциального рассеяния мы имеем (соотношения (3.27) и (7.76))

σ = ∑ℓσℓ ;     σℓ = (2ℓ + 1)|Sℓ − 1|2 ,

(16.10)

где параметры S_ℓ определяются фазами соответствующих волн:

Sℓ = ;

(16.11)

k − это импульс падающей частицы.
    Обобщим, учитывая соотношение (16.9), формулу (16.10) на многоканальный случай:

σba = ∑ℓ(2ℓ + 1)<b|Ŝℓ|a> − δba|2 .

(16.12)

В частности, для сечения упругого рассеяния в многоканальном случае получаем:

σelas = σaa = ∑ℓ(2ℓ + 1)|Sℓ − 1|2 ;

(16.13)

здесь мы ввели обозначение:

    Для сечения неупругого столкновения (т.е. неупругого рассеяния или реакции с перераспределением частиц) из (16.12) получаем

σba = ∑ℓ(2ℓ + 1)<b|Ŝℓ|a>|2 ;  b ≠ a.

(16.15)

    Часто приходится иметь дело с суммарным сечением всех неупругих процессов (его называют сечением реакций). Учитывая следствие (16.5) соотношения унитарности, мы можем выразить сечение реакций через диагональные элементы матрицы рассеяния:

(16.16)

Отсюда видно, что сечение реакции обращается в ноль, если все диагональные элементы
S-матрицы равны по модулю единице:

Это условие эквивалентно известному в теории потенциального рассеяния условию вещественности фаз. Если же какие-то неупругие процессы разрешены, т.е. σ_r ≠ 0, то, по крайней мере, для некоторых ℓ имеет место неравенство:

Если соотношение (16.11), введенное в теории потенциального рассеяния, использовать и в многоканальной теории в качестве соотношения, связывающего элементы S-матрицы с фазами рассеяния, то условию (16.18) будут соответствовать комплексные значения фаз δ_ℓ, причем их мнимая часть всегда положительна: Imδ_ℓ > 0. Выразим также через S-матрицу амплитуду упругого рассеяния:

(16.19)

Легко видеть, что соотношения (16.13), (16.16) и (16.19) согласуются с оптической теоремой (3.28).
    Итак, соотношение унитарности (16.1) позволяет выразить полное сечение всех неупругих процессов через параметры упругого рассеяния. Рассматривая внимательно выражения (16.13) и (16.16), можно сформулировать и нетривиальное качественное положение, относящееся к вопросу о соотношении упругих и неупругих процессов: невозможна ситуация, когда в результате столкновения происходят только неупругие процессы, не сопровождаемые упругим рассеянием. Действительно, сечение σ_elas обращается в нуль, только если все S_ℓ равны единице, но тогда и
σ_r = 0.
    Разнообразные физические примеры из ядерной и атомной физики показывают, что требование унитарности S-матрицы играет в теории исключительно важную роль. Очень часто обеспечение унитарности S-матрицы при выполнении приближённых расчетов резко улучшает качество совпадения теории с экспериментом. В связи с этим разработаны и продолжают разрабатываться специальные приемы «унитаризации» теории. Одним из них является использование так называемой K-матрицы, или K-оператора.
    Связь -оператора и Ŝ-оператора определяется соотношением:

(16.20)

при этом на -оператор наложено требование эрмитовости:

+ = .

(16.21)

Тогда любое приближенное выражение для -оператора автоматически дает унитарную S-матрицу.
    В качестве примера использования условия унитарности рассмотрим вопрос о так называемых пороговых явлениях. Пусть а обозначает упругий, а b − неупругий канал при столкновении частицы х с мишенью А. Обозначим величиной E_thres = ε_b − ε_а значение энергии частицы х, при котором открывается канал Ь. Оказывается, что в окрестности Е ≈ E_thres, сечение упругого рассеяния ааа обнаруживает характерные особенности, как бы «откликаясь» на открывающийся при Е = E_thres, неупругий канал.
    S-матрица рассматриваемой системы имеет вид

(16.22)

В области ниже порога происходит только упругое рассеяние; здесь из всех элементов S-матрицы (16.22) отличен от нуля лишь один − S_aa, и для него выполняется условие

В области выше порога соотношение унитарности (16.4) даёт связь между элементами S-матрицы:

Положим ради простоты, что орбитальный момент ℓ частицы х в обоих каналах а и b равен нулю, а между подсистемами х и А нет кулоновского взаимодействия. Тогда сечения упругого и неупругого рассеяний выражаются формулами:

σaa(E) = |Saa(E) − 1|2,

(16.25)

σba(E) = |Sba(E)|2,

(16.26)

где k_а = (2μE)^1/2 − импульс частицы в упругом канале. Вблизи порога E_thres энергетическая зависимость сечения неупругого рассеяния σ_ba(E) определяется прежде всего его зависимостью от быстро меняющегося импульса частицы в неупругом канале: k_b = (2μ(Е − E_thres))^1/2. Для того чтобы выяснить, как зависит S_ba(E) от k_b, воспользуемся снова соотношением унитарности (16.4) и свяжем с его помощью матричные элементы S_bb и S_ba

\S    Входящий сюда элемент S матрицы S_bb определяет упругое рассеяние частицы х в канале b, т.е. процесс ее упругого столкновения с возбужденной мишенью А* :

σbb(E) = |Sbb(E) − 1|2.

(16.28)

Фаза рассеяния в канале b, определенная общим соотношением (16.11), ведет себя при k_b → 0 согласно закону:

(16.29)

С учетом сделанного предположения, что ℓ = 0, отсюда получаем

(16.30)

Это хорошо известный в ядерной физике «закон 1/v», показывающий, что сечение экзотермической реакции при взаимодействии нейтральной частицы с ядром ведет себя вблизи порога обратно пропорционально скорости (импульсу) падающей частицы. Нам, однако, нужен сейчас не сам этот закон, а формула околопорогового поведения элемента S-матрицы в неупругом канале b, из которой этот закон вытекает

(16.31)

    Комбинируя вместе соотношения (16.24), (16.27) и (16.31), получаем, что вблизи порога при
Е > E_thres элемент S-матрицы S_aa(E) , определяющий сечение упругого рассеяния в канале а зависит от k_b согласно закону:

(16.32)

    Итак, для одной и той же величины |S_aa(E)| мы имеем в окрестности Е ≈ E_thres два выражения: (16.23) − ниже порога, (16.32) − выше порога. Считая, что элементы S-матрицы являются аналитическими функциями энергии (см. § 16.2), объединим эти два выражения общей формулой:

(16.33)

где − вещественная фаза, плавно меняющаяся в окрестности Е ≈ E_thres. Действительно, в узкой окрестности вблизи порога при Е > E_thres формула (16.33) непосредственно дает (16.32). Что касается области Е < E_thres, то здесь второе слагаемое в (16.39) мнимо, и, следовательно, отклонение величины |Saa(E) от единицы пропорционально уже не k_b, а , таким отклонением, как эффектом более высокого порядка, мы пренебрежем.
    Подставим теперь полученное выражение S_aa(E) в формулу (16.25) для сечения упругого рассеяния:

(16.34)

где

Отсюда видно, что если фаза заключена в интервале π/2 < < π (т.е. ctg() отрицателен), то сечение упругого рассеяния σ_аа(Е) имеет в точке Е = E_thres острый пик. Если фаза заключена в интервале 0 < < π/2, то кривая σ_аа(Е) в точке Е = E_thres претерпевает излом. Это и есть так называемые пороговые особенности в сечении упругого рассеяния.

§ 16.2. Дисперсионные соотношения

    В предыдущем параграфе мы воспользовались свойством аналитичности S-матрицы, рассматриваемой в качестве функции энергии (импульса) частицы в комплексной области изменения этих переменных. Требование аналитичности, предъявляемое к элементам S-матрицы, амплитуде рассеяния, t-матрице, относится к числу фундаментальных положений теории. Существует тесная связь между требованием аналитичности и одним из самых общих физических принципов − принципом причинности (см., например, [14]). Используя требование аналитичности, оказывается возможным записать для амплитуды рассеяния, элементов S-матрицы и т.п. особого рода интегральные соотношения − так называемые дисперсионные соотношения, играющие в современной квантовой теории очень важную роль.
    Разберем их смысл на примере дисперсионных соотношений для амплитуды упругого рассеяния вперед. Амплитуда ƒ(k, θ = 0) = ƒ(k,0) связана с S-матрицей соотношением

(16.36)

Особенности S-матрицы как функции энергии S(E) в комплексной плоскости Е нам известны
(см. § 6.4 и 12.3): это полюса на отрицательной вещественной полуоси:

соответствующие связанным состояниям системы, и полюса в 4-м квадранте плоскости Е , соответствующие квазистационарным состояниям системы (резонансам). Отсюда следует, что во всей верхней полуплоскости комплексной переменной k = (2μE)^1/2 особенностями S-матрицы и амплитуды рассеяния (16.36) являются полюса, расположенные на мнимой оси:

и отвечающие связанным состояниям (16.37). Рассмотрим интеграл

(16.39)

где контур С составим из вещественной оси и дуги большого круга в верхней полуплоскости. Вычитание амплитуды ƒ(∞,0) (совпадающей с борновской амплитудой рассеяния вперед) обеспечивает сходимость интеграла при больших k'.
    Если точка к лежит в верхней полуплоскости, то по теореме Коши получаем

(16.40)

где последнее слагаемое есть сумма по всем связанным состояниям системы; параметры r_n пропорциональны вычетам S-матрицы в полюсах (16.38). Если точку к устремить на вещественную ось, соотношение (16.40) несколько изменяется:

(16.41)

где знак соответствует интегралу в смысле главного значения.
    Запишем (16.41) отдельно для вещественной и мнимой частей амплитуды рассеяния вперед:

(16.42)

(16.43)

    Оптическая теорема позволяет вычислить мнимую часть амплитуды рассеяния вперед через полное сечение взаимодействия:

Дисперсионное соотношение (16.42) позволяет сделать то же для вещественной части:

(16.45)

    Правда, сюда входят также вычеты S-матрицы в полюсах, отвечающих связанным состояниям системы. Можно, однако, показать, что все они связаны с такими физическими характеристиками этих состояний, которые в принципе можно измерить (см. упр. 16.2).

§ 16.3. Обращение времени. Связь сечений прямого и обратного процессов при столкновении

Начнем с частного случая: рассмотрим процесс неупругого рассеяния частицы х + А → х' + А* . Если воспользоваться методом искаженных волн, то дифференциальное сечение парциального перехода |0> → |n> можно вычислить по формуле (11.9). Перепишем ее, слегка изменив обозначения. Пусть индекс а относится к каналу, где мишень А находится в основном, а индекс b − в возбужденном состоянии:

(16.46)

    Формула (16.46) дает вероятность такого процесса неупругого рассеяния, когда падающая частица имеет импульс k_a, рассеянная − импульс k_b, а мишень А переходит из состояния |а> в состояние |b>. Рассмотрим теперь процесс, обратный по времени: пусть частица импульсом (−k_b) (направленным противоположно импульсу k_b) падает на мишень, находящуюся в состоянии |b>, так что в результате столкновения мы имеем мишень в состоянии |а>, а рассеянную частицу − с импульсом (−k_a). Дифференциальное сечение такого обратного процесса дается (если по-прежнему пользоваться методом искаженных волн) все той же формулой (11.9). А именно:

(16.47)

    Как связаны между собой вероятности прямого и обратного процессов?
    Вспомним, что функции ψ⁽⁺⁾(r) и ψ⁽⁻⁾(r) удовлетворяют соотношению

(16.48)

Используя его, запишем входящий в (16.47) интеграл по-другому:

(16.49)

(последнее равенство получено с учетом эрмитовости оператора (ξ,r)). Хотя вьфажения (16.49) и очень близки, но не совпадают с интегралом, входящим в (16.46). Таким образом, между величиной сечений процессов а → b и b → а в общем случае нет какого-либо простого соотношения. Однако если состояния мишени |а> и |b> описываются вещественными волновыми функциями (конечно, какой-либо постоянный общий фазовый множитель при этом несуществен), то интеграл (16.49) и интеграл, входящий в (16.46) совпадают другом с другом. В этом случае сечения процессов связаны между собой простым соотношением

(16.50)

Условие вещественности волновых функций состояний |а> и |b> выполняется, например, в случае, когда угловые моменты обоих состояний равны нулю:

или когда хотя бы проекции этих моментов равны нулю:

    Мы начали с частного случая, выбрав конкретный тип столкновения и конкретный приближенный метод его описания. Возьмем от полученного здесь результата указание на то, что вопрос о существовании соотношения, связывающего между собой сечения прямого и обратного процессов, каким-то образом связан с вопросом об угловых моментах (спинах) сталкивающихся подсистем. И поэтому, переходя к общему рассмотрению, наделим и сталкивающиеся и образующиеся в процессе столкновения частицы спинами. Учтем (подробнее см., например, в
[1, § 58]), что при обращении времени (t → − t) проекции всех угловых моментов (спинов) меняют знак:

    Рассмотрим столкновение частиц 1 и 2 с образованием частиц 3 и 4:

а также процесс

который является обратным по отношению к (16.54). В качестве физических величин, задающих состояние, возьмем импульс k относительного движения двух частиц и проекции спинов частиц на ось z . Тогда амплитуду процесса (16.54) можно представить в виде

ƒ(а → b) ~ <kb,m3,m4|Ŝ − |-ka,m1,m2> ,

(16.56)

где индекс а относится к паре частиц (1 + 2), а индекс b − к паре частиц (3 + 4). Соответственно для амплитуды обратной реакции (16.55) имеем

ƒ(b → b) ~ <-ka,m1,m2|Ŝ − |-kb,m3,m4> ,

(16.57)

    Как известно, уравнения движения консервативной системы в классической механике инвариантны относительно изменения знака времени. Отсюда вытекает исключительно важное свойство движения: если система при увеличении времени t проходит некоторую последовательность состояний, то для этой системы возможно и обращенное движение, когда при увеличении t она проходит эти же состояния в обратной последовательности с противоположным направлением импульса и момента импульса. Аналогичный принцип обратимости движения имеет место и в квантовой механике. Из него вытекает важное соотношение для амплитуд вероятностей прямого и обратного процессов:

которое называется теоремой взаимности. Эта теорема устанавливает связь между прямым процессом и таким процессом, который отличается от обратного противоположном знаком проекций спинов. Следовательно, теорема взаимности, вообще говоря, не позволяет связать друг с другом амплитуды прямой (16.56) и обратной (16.57) реакций. Однако можно установить связь между дифференциальными сечениями этих реакций, усредненными по проекциям спинов в начальном состоянии и просуммированными по проекциям спинов в конечном состоянии (именно также сечения измеряются в случае, когда сталкивающиеся частицы не поляризованы, а детекторы не чувствительны к поляризации регистрируемых частиц). Согласно (16.56) и (16.57), для этих усредненных сечений имеем

(16.59)

(16.60)

где s_i − спины частиц. Исключая с помощью теоремы взаимности (16.58) входящие в (16.59) и (16.60) матричные элементы S-матрицы, получаем

(16.61)

    Если спины всех частиц равны нулю, отсюда следует соотношение (16.50).

Соотношение (16.50) называется соотношением детального баланса. Оно играет фундаментальную роль в физике, поскольку устанавливает связь между вероятностями прямых и обратных процессов. Иногда и соотношение (16.61) называют соотношением детального баланса, но надо помнить, что оно устанавливает связь только между усредненными дифференциальными сечениями этих процессов.

Упражнения

16.1. Показать, что если неупругий канал связан с разлетом заряженных частиц, то пороговые особенности в сечении упругого рассеяния, описываемые выражением (16.34) сглаживаются.

16.2. При взаимодействии частиц высокой энергии с ядрами (kR >>» 1) орбитальный момент частицы ℓ и прицельный параметр b связаны между собой соотношением классической механики:
(ℓ = kb) . Заменяя S-матрицу (16.11) S_матрицей, зависящей от b, параметризуя ее согласно модели «черной» сферы (15.4):

(16.62)

и переходя в формулах (16.13) и (16.16) от суммирования по £ к интегрированию по Ъ, получить результаты (15.11) − (15.13):

16.3. В условиях предыдущего упражнения вычислить амплитуду упругого рассеяния частицы. Воспользоваться предельным соотношением для полиномов Лежандра:

где J₀(x) − функция Бесселя нулевого порядка. Сравнить полученный результат с (15.8).

16.4. Используя результат упражнения (6.5), показать, что вычет S-матрицы r_r в полюсе Е_n связан с амплитудой асимптотики («хвоста») волновой функции соответствующего связанного состояния:

(16.65)

16.5. Раскрыть смысл соотношения (16.48) с точки зрения операции обращения времени.

16.6. Рассмотреть результат упражнения (7.1) с точки зрения вопроса о соотношении вероятностей прямых и обратных процессов.