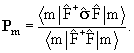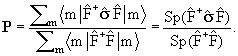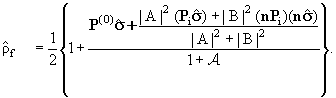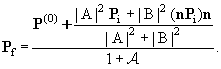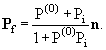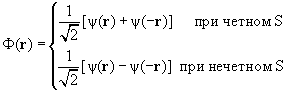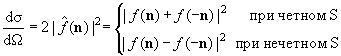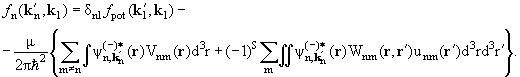Лекция 17. Эффекты взаимодействий, зависящих от спина. Тождественность частиц

§ 17.1. Инвариантные свойства амплитуды рассеяния частиц со спином. Поляризация частиц при рассеянии

    В этом параграфе будет показано, что анализ свойств симметрии взаимодействия позволяет получить общий вид амплитуды рассеяния и установить целый ряд важных особенностей процесса рассеяния. В частности, явление поляризации частиц при рассеянии находит достаточно полное объяснение в рамках теоретического рассмотрения, опирающегося на анализ одних лишь свойств инвариантности амплитуды рассеяния. Для простоты ограничимся случаем, когда налетающая частица имеет спин s = 1/2, а частица-мишень спином не обладает.
    Предположим, что до рассеяния налетающая частица находилась в состоянии χ_sm c определенным значением m проекции спина на ось z . Стационарная задача потенциального рассеяния частицы со спином состоит в решении стационарного уравнения Шредингера с дополнительным условием

где ψ(r), как и χ_sm − столбец из (2s + l) элементов. Повторяя выкладки § 1.1, получим для асимптотики волновой функции, удовлетворяющей этому граничному условию, выражение

(17.2)

где k' = kr/r. Интеграл

(17.3)

есть амплитуда расходящейся волны, которая теперь зависит не только от энергии падающей частицы и угла рассеяния, но и от спиновой переменной, и играет роль спиновой функции рассеянной частицы.
    Формулу (17.2) удобно записать еще и по-другому:

(17.4)

где оператор (k',k), будем называть оператором амплитуды рассеяния. Для нахождения его явного вида надо решить задачу рассеяния на потенциале (r), который представляет собой оператор, действующий не только в пространственном (импульсном), но и в спиновом пространстве частицы.
    Решение такой задачи рассеяния в общем случае представляет собой сложную проблему. Однако некоторые важные данные о структуре оператора (k',k) можно получить путем анализа свойств симметрии взаимодействия, поскольку амплитуду процесса столкновения можно представить в виде матричного элемента оператора рассеяния Ŝ:

<m' |(k',k)| m> ~ (l/k)<m',k' |Ŝ − | m,k> ,

(17.5)

а свойства симметрии S-матрицы совпадают со свойствами симметрии гамильтониана системы Ĥ. Гамильтониан системы, состоящий из подсистем, связанных сильным или электромагнитным взаимодействием, инвариантен относительно произвольных поворотов и пространственной инверсии . Следовательно, и оператор амплитуды должен быть инвариантен относительно этих преобразований.
    Опираясь на эти фундаментальные свойства оператора (k',k), найдем его общий вид. Ограничимся случаем s = 1/2 . Поскольку является оператором в пространстве спиновых функций с s = 1/2 его всегда можно представить в виде линейной комбинации матриц Паули _i и единичного оператора , которые образуют в этом пространстве полный набор операторов:

(17.6)

здесь A(k',k) и β_i(k',k) − некоторые функции k и k'. Оператор амплитуды (17.6) будет инвариантом произвольного поворота и инверсии только в том случае, если A(k',k) будет скаляром, а величины β_i(k',k) − компонентами некоторого псевдовектора. Введем три единичных вектора:

(17.7)

Нетрудно проверить, что при k = k' они попарно ортогональны, а поэтому могут быть взяты в качестве базиса трехмерного пространства. Тогда вектор β можно представить в виде

где В, С, D − некоторые скалярные или псевдоскалярные функции кик'. При инверсии кик' изменяют знак, а поэтому изменяют знак также l и q. Поэтому из инвариантности оператора (17.6) относительно пространственной инверсии следует, что С = 0 и D = 0, а функции A(k',k) и В(k',k) − скаляры. Эти функции зависят от функции k и k' только через скалярные комбинации k² = k' ² и
(k' ·k ), т. е. являются функциями энергии Е и угла рассеяния θ. Таким образом, оператор амплитуды рассеяния имеет следующий общий вид:

(k',k) = A(E,θ) + B(E,θ)(n·),

(17.9)

где n − единичный вектор нормали к плоскости рассеяния. Явный вид функций A(E,θ) и B(E,θ) определяется спецификой взаимодействия. Дифференциальное сечение рассеяния на угол θ в случае, когда проекция спина частицы на ось z в начальном состоянии равна т, а в конечном − m', дается формулой

dσm'm/dΩ = |<m' |(k',k)| m>|2 = |A(E,θ)δm'm + <m' |n·| m>|2.

(17.10)

    Если детектор, регистрирующий рассеянные частицы, не чувствителен к проекции спина этих частиц, наблюдаемое в этом случае дифференциальное сечение следует вычислять, просуммировав выражение (17.19) по всем возможным значениям m' :

Используя (17.10), находим

= |A(E,θ)|2 + |B(E,θ)|2 + 2Re(A*B)<m' |n·| m>.

(17.12)

Отсюда видно, если падающий поток частиц поляризован, а Re(A^*B) ≠ 0, то вероятность рассеяния зависит не только от полярного угла рассеяния θ, но и от направления вектора n.
    Если пучок падающих частиц не поляризован, то в нем с одинаковыми вероятностями представлены частицы с различными значениями m. Для вычисления дифференциального сечения рассеяния таких частиц следует усреднить (17.11) по m:

= ∑m <m|+|m> = Sp(+).

(17.13)

В этом случае сечение выражается через след матрицы оператора ⁺. Используя известные свойства матриц Паули, получаем

= |A(E,θ)|2 + |B(E,θ)|2 .

(17.14)

    Теперь допустим, что детектор чувствителен к значению проекции спина регистрируемой частицы. Тогда можно измерить распределение этой величины для частиц, рассеянных в данном направлении. Для характеристики этого распределения принято использовать величину среднего значения спина, которая называется вектором поляризации и определяется следующим образом:

Р =  ,

(17.15)

где ¹/₂ − вектор спина, а черта означает усреднение по его проекции.
    Сперва предположим, что все частицы падающего пучка находятся в состоянии с определенным значением m проекции спина на ось z. В этом случае вектор поляризации рассеянных частиц есть

(17.16)

    Пусть теперь в падающем пучке различные значения т представлены с одинаковыми вероятностями, т.е. вектор поляризации бомбардирующих частиц равен нулю. В этом случае для вычисления вектора поляризации Р рассеянных частиц надо произвести усреднение вектора Р_m, учитывая равные статистические веса разных проекций спина т в начальном состоянии:

(17.17)

Наконец, подставляя сюда (17.9), окончательно получаем

(17.18)

    Итак, в результате рассеяния первоначально неполяризованного пучка частиц со спином
s = 1/2 на бесспиновых частицах, вообще говоря, происходит поляризация частиц. Она зависит от энергии частиц Е и угла рассеяния θ. При этом вектор поляризации Р всегда направлен перпендикулярно плоскости рассеяния, а его абсолютная величина существенно зависит от значения Re(A^*B).
    Обращаясь к (17.18) и (17.12), мы видим, что поляризация возникает при тех же условиях, при которых имеет место азимутальная асимметрия рассеяния поляризованных частиц. Поляризационный эффект существенно зависит от относительной фазы амплитуд А(E,θ) и
В (E,θ) и обращается в нуль, если одна из них равна нулю.

§ 17.2. Рассмотрение поляризационных явлений на основе аппарата спиновой матрицы плотности

    Способ рассмотрения поляризации при столкновениях, которым мы пользовались в предыдущем параграфе, является хотя и наглядным, но в техническом отношении довольно громоздким. Те же, а также и другие, более общие результаты можно получить с помощью аппарата спиновой матрицы плотности. Такой способ является, как мы увидим, и не менее физичным и, несомненно, более изящным с точки зрения математики.
    Как известно (см., например, [1, § 45]), спиновое состояние частицы со спином s = 1/2 характеризуется в самом общем случае матрицей плотности размерности 2×2:

= 1/2(1 + Р·) ,

(17.19)

где − вектор из трех матриц Паули, а Р − числовой вектор, указывающий среднее направление и среднюю величину вектора спина частиц в рассматриваемом состоянии:

Модуль этого вектора Р = |Р| есть степень поляризации частицы. Только при Р = 1 матрица плотности (17.19) удовлетворяет критерию чистого состояния ² = ; в этом случае всегда можно указать такое направление, проекция спина на которое имеет определенное значение +1/2 или −1/2; другими словами, в этом случае спиновое состояние частицы можно описать некоторой одной волновой функцией (вектором состояния). В противоположном случае, когда Р = 0, спиновая матрица плотности (17.19) пропорциональна единичной матрице. Такая матрица плотности описывает неполяризованную систему: никакое направление в пространстве не выделено по отношению к любым спиновым характеристикам состояния. В промежуточном случае 0 < Р < 1 мы имеем дело с частично поляризованной системой. Во всех случаях, кроме Р = 1, спиновое состояние частицы является смешанным.
    Применяя аппарат спиновой матрицы плотности в теории столкновений, мы ограничимся простейшим случаем рассеяния частицы со спином s = 1/2 на неподвижном силовом центре (частице со спином s = 1/2) . Пусть матрицы

i = 1/2(1 + Рi·)

(17.21)

и

f = 1/2(1 + Рf·)

(17.22)

характеризуют спиновое состояние частиц до и после столкновения. Согласно общим правилам, матрицу плотности конечного состояния _f, можно выразить через матрицу плотности начального состояния _i по формуле

f ~ i+,

(17.23)

где = (k',k) − амплитуда рассеяния (или, как мы говорили в предыдущем параграфе, оператор амплитуды рассеяния), для которой в рассматриваемом случае справедлива формула (17.9).
    Дифференциальное сечение рассеяния частиц безотносительно к их поляризации в конечном состоянии дается выражением

dσ/dΩ = Spi+,

(17.24)

Подставим сюда (17.21) и (17.19):

Мы получили формулу, обобщающую уже известный результат (17.9) и (17.14) для случаев полностью поляризованного (P_i = 1) и неполяризованного (P_i = 0) падающих пучков. Из нее видно, что рассеяние частично поляризованных частиц, вообще говоря, азимутально асимметрично; условием возникновения азимутальной асимметрии является наличие интерференции между амплитудами рассеяния А(Е,θ) и В(Е,θ):

Формулу (17.25) можно записать еще и по-другому:

dσ/dΩ = dσ(0)/dΩ{1 + P(0)Pi} ≡ dσ(0)/dΩ{1 + }

(17.27)

Сюда вошли уже знакомые нам величины − дифференциальное сечение рассеяния неполяризованных частиц (формула (17.14)):

и вектор поляризации этих частиц после рассеяния (формула 17.18)):

(17.29)

Коэффициент

(17.30)

будем называть коэффициентом азимутальной асимметрии рассеяния. Из (17.30) видно, что составляющая вектора поляризации падающих частиц, лежащая в плоскости рассеяния (в частности, продольная составляющая по отношению к импульсу падающих частиц), не дает никакого вклада в рассеяние. Уместно подчеркнуть, что выводы, к которым мы пришли, основаны исключительно на симметрийных соображениях о процессе столкновения.
    Теперь рассмотрим вопрос, которого мы в предыдущем параграфе совсем не касались, о поляризации частиц в конечном состоянии при рассеянии частично поляризованных частиц. Здесь достоинства аппарата спиновой матрицы плотности проявляются особенно ярко.
    Нормируем матрицу плотности конечного состояния согласно общепринятому условию:

Spf  = 1 .

(17.31)

Тогда, снова подставляя (17.21) и (17.9) в (17.23), получаем

(17.32)

Учитывая общую форму матрицы плотности (17.22), получаем выражение для вектора поляризации рассеянных частиц:

(17.33)

В числителе мы видим два слагаемых. Первое, Р⁽⁰⁾ = Р⁽⁰⁾n, не связано с наличием поляризации падающих частиц. Второе, пропорциональное степени поляризации падающих частиц P_i представлено в виде суммы двух компонент − вдоль вектора P_i, с весом |A|²/(|A|² + |В|²) , и вдоль нормали к плоскости рассеяния n с весом |В|²/(|A|² + |В|²).
    В частном случае, когда сам вектор P_i направлен по n т.е. P_i = P_in, имеем

(17.34)

Отсюда видно, что при рассеянии частично поляризованных частиц (0 < |P_i| < 1) возможно как увеличение степени их поляризации ( |P_f| > |P_i|), так и их частичная деполяризация (|P_f| < |P_i|) , причем переход от одного случая к другому соответствует изменению знака направления вектора начальной поляризации P_i относительно вектора n. В предельном случае, когда пучок падающих частиц полностью поляризован перпендикулярно плоскости рассеяния (P_i = ±n) , деполяризации частиц при рассеянии не происходит.

§ 17.3. Рассеяние тождественных частиц

    До сих пор мы предполагали, что сталкивающиеся частицы различны. Поэтому, вводя понятие дифференциального сечения рассеяния, мы считали возможным отделить случай рассеяния в заданном направлении Ω частицы из падающего пучка от случая рассеяния в этом направлении частицы мишени. Если же сталкивающиеся частицы тождественны, этого сделать нельзя. Будем называть дифференциальным сечением рассеяния тождественных частиц величину dσ(Ω) равную отношению потока dI(Ω) любых частиц, вылетающих в телесный угол dΩ, к плотности потока падающих частиц относительно мишени. Пользуясь Ц-системой, поток частиц, вылетающих в направлении п, можно представить в виде

dI(Ω) = jin|(n)|2dΩ +  jin|(-n)|2dΩ ,

(17.35)

где (n) − амплитуда рассеяния, которая должна определяться из асимптотики соответствующим образом симметризованной волновой функции. В соответствии с нашим определением дифференциального сечения рассеяния тождественных частиц отсюда получаем

dσ(Ω) = (|(n)|2 +  |(-n)|2)dΩ .

(17.36)

Найдем амплитуду рассеяния (n). Пусть Ψ(r,m₁,m₂) есть волновая функция, описывающая движение тождественных частиц в Ц-системе. Здесь

определяется координатами r₁ и r₂ налетающей частицы и частицы-мишени, а m₁ и m₂ − проекции спинов сталкивающихся частиц на ось z. Представим волновую функцию в виде

где Ф(r) − координатная функция, χ_SM(m₁,m₂) − спиновая функция, S − суммарный спин двух частиц, М − его проекция на ось z. Волновая функция системы двух тождественных частиц должна быть либо симметричной, либо антисимметричной относительно перестановки частиц в зависимости от того, являются они бозонами или фермионами, т.е. имеют целый или полуцелый спин s. Из (17.37) видно, что при перестановке, частиц вектор r меняет знак. Поэтому волновая функция системы двух тождественных частиц должна удовлетворять условию

Знак спиновой функции при перестановке переменных двух частиц определяется формулой

Тогда из (17.38) и (17.39) получаем

Следовательно, координатная функция системы из двух тождественных частиц должна быть четной при четном S и нечетной при нечетном S. Поэтому, если четность является интегралом движения, суммарный спин S системы сохраняется.
    В связи с этим имеет смысл рассмотреть столкновение двух тождественных частиц, находящихся в состоянии с определенным значением S суммарного спина. Пусть ψ(r) есть волновая функция, описывающая движение частицы в Ц-системе. Тогда симметризованную функцию Ф(r) в соответствии с (16.86) можно представить в виде

(17.42)

где множитель 1/√2 выбран из условия, чтобы плотность потока падающих частиц в состоянии Ф равнялась плотности потока в состоянии ψ. Рассматривая асимптотику функции (17.42), получаем амплитуду рассеяния тождественных частиц:

(17.43)

где ƒ(n) − коэффициент при расходящейся сферической волне в асимптотике функции ψ(r) . Подставляя это выражение в (17.36), находим дифференциальное сечение:

(17.44)

В частном случае рассеяния тождественных частиц, связанных центрально-симметричным взаимодействием, отсюда получаем

Это сечение симметрично относительно θ = π/2, что является прямым следствием неразличимости сталкивающихся частиц. Заметим, что при θ = π/2 дифференциальное сечение рассеяния в состоянии с нечетным S равно нулю. В то же время при четном S сечение рассеяния оказывается, как это видно из (17.45), в 4 раза больше сечения |ƒ|², которое следовало бы ожидать для нетождественных частиц. Запишем (17.45) по-другому:

В этом виде дифференциальное сечение, даваемое квантовой теорией, удобно сравнить с тем, которое получается в классической механике для столкновения двух одинаковых частиц:

Здесь первое слагаемое есть сечение рассеяния под углом θ частиц из падающего пучка, а второе слагаемое − сечение рассеяния тех же частиц под углом π − θ, равное сечению рассеяния под углом θ частиц мишени. Третье же слагаемое в выражении, (17.46) не имеет аналога в классической механике. Этот член описывает существенно квантовое явление − интерференцию амплитуд рассеяния под углами θ и π − θ. Его называют обменным членом. При θ = π/2 абсолютная величина обменного члена равна оставшейся части дифференциального сечения, которую по аналогии с (17.47) можно назвать «классической частью». При нечетном S они погашают друг друга и квантовое сечение равно нулю, а при четном S за счет обменного члена квантовое сечение в 2 раза больше «классической части».
    До сих пор предполагалось, что сталкивающиеся частицы находятся в состоянии с определенным значением суммарного спина S. Если же падающий пучок и мишень поляризованы, то наблюдаемое сечение будет сечением, усредненным по различным начальным спиновым состоянием. Рассмотрим этот вопрос на примере столкновения двух частиц со спином 1/2. Поскольку суммарный спин сохраняется, усредненное сечение можно представить в виде

(17.48)

3/4 − статистический вес триплетных состояний, а 1/4 − синглетного состояния. Подставляя сюда (17.44), получаем

Таким образом, обменный эффект проявляется при рассеянии не только поляризованных, но и неполяризо-ванных частиц.

§ 17.4. Эффекты тождественности частиц при столкновении составных систем

    Учет тождественности частиц при описании электрон-атомных столкновений или ядерных реакций под действием нуклонов вносит существенное усложнение в аппарат теории. С тождественностью сталкивающихся частиц связан также ряд особых физических эффектов, представляющих большой интерес и в атомной, и в ядерной физике.
    Рассмотрим сначала на простейшем примере взаимодействия электронов с атомом водорода, как модифицируются при учете тождественности электронов уравнения многоканальной задачи рассеяния, которые мы получили в § 10.1. Для этого полную волновую функцию всей системы, которую мы, согласно (10.2), должны разложить по полному набору атомных волновых функций, запишем явно как функцию координат двух электронов − налетающего и атомного:

    В предыдущем параграфе было показано, что суммарный спин двух электронов 5, а вместе с ним и четность их координатной волновой функции относительно перестановки r₁ ↔ r₂ сохраняется в процессе столкновения:

Это значит, что вместо разложения (10.3) мы должны использовать разложение по симметризованному базису:

где φ_n(r) − волновые функции стационарных состояний атома водорода (как и раньше, подразумевается, что знак ∑ в (17.52) обозначает и бесконечную сумму по дискретному спектру, и интеграл по непрерывному спектру). При этом искомые канальные функции u_n(r) по-прежнему удовлетворяют асимптотическим условиям (10.7).
    Полный гамильтониан рассматриваемой системы имеет вид

(17.53)

    Подставим (17.52) и (17.53) в стационарное уравнение Шредингера (10.1). Умножая обе части этого уравнения на функцию φ*_n(r₂) и интегрируя по r₂ с учетом ортонормированности базиса φ_n(r), получаем вместо дифференциальных уравнений (10.4) систему связанных интегродифференциальных уравнений для канальных функций u_n(r):

(17.54)

(17.55)

(17.56)

Функции W_nm(r,r' ) , входящие в интегральную часть уравнений, выражаются через атомные волновые функции и другие известные величины:

(17.57)

Система уравнений (17.54) при ограниченном числе учитываемых каналов (m,n = 1,2, ... , N) вместе с дополнительными условиями (10.7) выражает приближение сильной связи каналов с учетом обмена.
    Свойства канальных функций u_n(r), удовлетворяющих системе уравнений (17.54), в том числе и их асимптотические свойства при r → ∞,

(17.58)

т.е. значения амплитуд упругого или неупругого рассеяния , зависят от суммарного спина S налетающего и атомного электронов. Если падающий пучок электронов неполяризован, то веса триплетного и синглетного состояний пары электронов равны соответственно 3/4 и 1/4, и дифференциальное сечение рассеяния дается выражением

(17.59)

Частным случаем приближения сильной связи с обменом является так называемое приближение замороженного остова, которое довольно широко используется в расчетах упругого рассеяния электронов на атомах. При таком подходе в правой части выражения (17.54) сохраняет лишь единственное слагаемое, отвечающее основному состоянию атома, и волновая функция рассеиваемого электрона удовлетворяет интегродифференциальному уравнению

(17.60)

Упражнения

17.1. В борновском приближении найти усредненное по поляризации дифференциальное сечение рассеяния частиц со спином s = 1/2 на потенциале со спин-орбитальным взаимодействием:

V = V₁(r) + V₂(r)(ℓ · ŝ).

Описывает ли борновское приближение поляризацию рассеянных частиц?

17.2. Используя гриновский оператор , найти формальное решение уравнения (17.54) и его асимптотику. Показать, что точное выражение амплитуды рассеяния при использовании приближения сильной связи с обменом имеет вид

(17.62)

Сравнить с выражениями (10.26) и (10.29), полученными без учета обмена.

17.3. Используя (17.62), найти амплитуду рассеяния электрона на атоме водорода в борновском приближении с учетом обмена (приближение Борна − Оппенгеймера).

17.4. Показать, что благодаря обменным эффектам при неупругом рассеянии электронов атомом гелия оказываются возможными, даже в отсутствие спиновых слагаемых в гамильтониане системы, переходы с изменением полного спина атома.