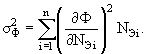Статистика регистрации частиц

    Ядерные взаимодействия относятся к дискретным случайным событиям пуассоновского типа. При достаточно большом среднем числе наблюдаемых событий вероятность того, что в течение времени t произойдет N событий, равна

где ν − средняя интенсивность потока частиц.
    В среднем число наблюдаемых событий

Дисперсия

    При зарегистрированном числе событий N₃ (N₃ >> 1) величины , ν и D оцениваются как

= N_Э,  ν = N_Э /t,   D = N_Э.

    Доверительный интервал ΔN, соответствующий доверительной вероятности ~70% и называемый среднеквадратичным интервалом или среднеквадратичной ошибкой σ, оценивается как

σ = (N_Э)^1/2.

    Истинная величина  с вероятностью ~70% заключена в интервале

N₃ − σ ≤ ≤ N₃ + σ.

Для величины Ф, являющейся функцией случайных величин N₁, …, N_n, среднее значение равно

= Ф(₁, …, _n) = Ф(N_Э1, …, N_Эn),

а дисперсия −

    Дисперсия оценки величины интенсивности потока частиц ν = N/t

σ_ν² = ν/t.

Относительная ошибка, соответствующая доверительной вероятности 70%

δ_ν = (N_Э)^-1/2.

Задачи

П 6.1.  Если при регистрации радиоактивного распада среднее число отсчетов в секунду равно 6, то какова вероятность зарегистрировать 10 импульсов в секунду?

П 6.3.  В эксперименте при реконструкции инвариантной массы пары e⁺e⁻ было обнаружено 36 событий Jψ → e⁺e⁻, средняя масса составила 3 100 МэВ. Какова ошибка измерения, если точность аппаратуры составляет Δm/m = 1% ?

П 6.5.  За 10 мин детектор зарегистрировал 2121 импульс. Указать доверительный интервал (с доверительной вероятностью 70%) для оценки интенсивности источника.

П 6.6. Сколько импульсов должен зарегистрировать детектор, чтобы гарантировать ошибку в 3% при определении интенсивности потока событий?

П 6.7. Рассчитать среднее время между регистрациями двух событий и дисперсию, если интенсивность событий равна 10 имп/сек.

П 6.8. Активность источника излучения в среднем равна 90 имп/мин. Какова вероятность того, что измеренная скорость счета будет составлять 80 имп/мин, 120 имп/мин.?

П 6.9.  Интенсивность излучения источника в одном направлении 160 имп/мин, а в направлении, перпендикулярном к первому, – 20 имп/мин. Сколько времени следует затратить на измерение той и другой интенсивности, если их отношение требуется определить с точностью 1%?

П 6.10.       Интенсивность излучения радиоактивного источника около 5·10² имп/мин. Сколько времени следует затратить на ее измерение с точностью 1%? Время измеряется секундомером с ценой деления 0,5 с.

П 6.11.       Каковы среднеквадратичная и относительная ошибки в определении интенсивности излучения источника, если суммарная интенсивность (источник + фон) измерялась 1 час и составила 362 имп/мин, а интенсивность фона - 31.2 ±0.4 имп/мин?

П 6.12.       Определите скорость счета случайных совпадений для схемы с разрешающим временем 10 нс, если загрузка одного из трактов 102 импульса в секунду, а второго 28 импульсов в секунду.

П 6.13.       Два измерительных тракта регистрируют частицы от независимых источников. Один с частотой 3000 импульсов в секунду, а второй – 5000 импульсов в секунду. После подсоединения их к схеме совпадения за одну минуту было зарегистрировано 12 случайных совпадений.Определить разрешающее время схемы совпадений.

П 6.14.       Черенковский счетчик создает 20 фотонов на частицу. Фотоумножитель конвертирует фотоны в фотоэлектроны с эффективностью 10%. Каждый фотоэлектрон создает сигнал. Какова вероятность того, что частица, попавшая в счетчик, не приведет к созданию сигнала? Сколько частиц из 1000 останется не зарегистрированными?
Ответ:  N = 122