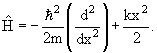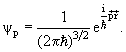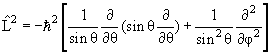Семинар 3. Модель Бора. Состояния в классической и квантовой физике. Квантовая статистика. Исходя из представлений
классической физики и дополнив ее квантовыми постулатами, Н. Бор создал модель
атома, в которой электроны находились в определенных стационарных состояниях,
что позволило объяснить устойчивость системы и дискретный характер атомных
спектров. Опыты Франка-Герца подтвердили правильность модели Бора.
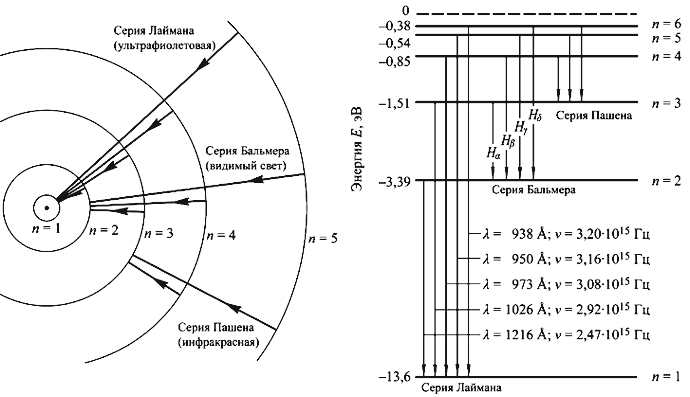
3.1. Модель Бора атома водородаВ модели Э. Резерфорда в центре атома расположено положительно заряженное массивное ядро размером R ≈ 10-12 см. Н. Бор предложил модель, которая впервые позволила удовлетворительно объяснить закономерность строения атома водорода. Основные постулаты теории Бора:
Движение по круговой орбите. Частота обращения ν:
Условие стационарной орбиты. Квантование углового момента:
Боровский радиус атома водорода (n = 1, Z = 1) r0 = ћ2/me2 = 0.529 Å Полная энергия электрона E квантуется:
Если электрон находится на 1-ой боровской орбите, то атом водорода находится в основном состоянии E0 = −me4/2ћ2 = −13.6 эВ. Энергия переходов (nf → ni)
Постоянная Ридберга
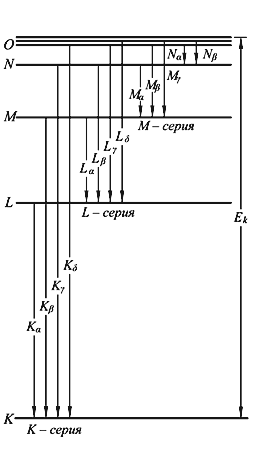
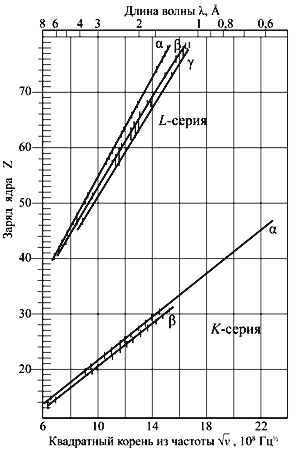
3.2. Рентгеновские спектры. Закон Мозли В химических элементах электроны
распределяются по электронным орбитам в соответствии с принципом Паули. Если из
атома с орбиты n = 1 выбивается электрон, то вакансия заполняется электронами с
более высоких орбит с n = 2, 3 и т. д. Разность энергий этих орбит излучается в виде
фотонов, длина волны которых при больших Z будет
находиться в рентгеновском диапазоне.
Г. Мозли предположил, что
энергия и, следовательно, частота характеристического излучения должны зависеть
от квадрата атомного номера Z химического элемента.
где R – постоянная
Ридберга, σ – постоянная
экранирования, для легких элементов σ ≈ 1.
3.3. Эксперименты Франка-Герца Эксперименты Франка-Герца
подтвердили предположение Бора о том, что спектры атомов объясняются наличием
дискретных энергетических уровней, которые могут возбуждаться в результате
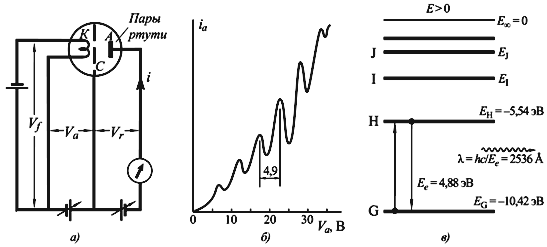
рассеяния электронов на атоме. E = Eh − E0 = −5.54 − (−10.42) = 4.88 эВ. Если энергия пучка медленных электронов, проходящего через пары ртути, меньше 4.88 эВ, то столкновения электронов пучка с атомами ртути будут упругими, т.е. без передачи энергии. Если энергия пучка электронов превышает 4.88 эВ, то происходят неупругие столкновения с передачей части энергии электрону атома ртути, сопровождающиеся переходами электронов атома ртути в первое возбужденное состояние. Поэтому в зависимости анодного тока от ускоряющего потенциала будут наблюдаться характерные максимумы и минимумы, соответствующие дискретным уровням энергии, на которых находятся внешние электроны атома ртути.
Рис. 3.4 Опыт Франка-Герца. а) Схема экспериментальной установки. В баллоне с
парами ртути имелись три электрода: К – катод, А – анод и С – сетка. Ускоряющая
разность потенциалов Vaприкладывалась между катодом и сеткой, между
сеткой и анодом создавалось тормозящее поле с 3.4. Состояния в классической и квантовой физике Теория атома Н. Бора правильно описала переходы в атоме водорода. Значение
радиуса первой боровской орбиты хорошо согласовывалось экспериментальными
оценками размера атома водорода. Однако она не могла объяснить относительную
интенсивность спектральных линий, а также структуру оптических спектров более
сложных атомов. В своей теории Бор правильно предугадал основные особенности
квантового строения атомов. Дальнейшее развитие квантовой физики показало, что
описание состояний системы в классической и квантовой физике различны. Квантовые
понятия отражают фактическую смену представлений о структуре материи, о свойствах ее фундаментальных составляющих.
Поиски ответов на эти проблемы привели к новому пониманию природы материи и
становлению квантовой физики.
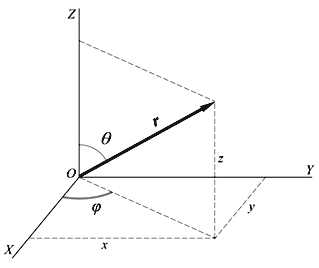
3.5. Волновая функция Состояние частицы в
классической физике в любой момент времени описывается заданием ее координат и
импульсов (x, y, z, px,py,pz).
Зная эти величины в момент времени t, можно описать эволюцию системы под
действием известных сил во все последующие и предыдущие моменты времени.
Координаты и импульсы частиц в классической физике являются непосредственно
измеряемыми величинам или наблюдаемыми.
В силу теории сложения вероятностей определение волновой функции необходимо дополнить условием нормировки ∫|ψ(x,y,z,t|2dV = 1, где интеграл, взятый по всему бесконечному пространству, − вероятность достоверно обнаружить частицу в момент времени t во всем пространстве. Возникает своеобразное двухступенчатое описание физических объектов: сначала нужно найти волновую функцию, а затем, уже по ней, определить значения наблюдаемых. В квантовой теории не все наблюдаемые одновременно могут иметь точно определенные значения. Например, квантовая частица не может иметь одновременно определенные значения импульса и координаты. 3.6. Уравнение движения свободной частицыВолновая функция свободно движущейся частицы с энергией E и импульсом p имеет вид
Константа A определяется из условия нормировки волновой функции A =(2πћ)-3/2. В тех случаях, когда
частица находится в области пространства, где действующие на нее силы равны нулю
(свободное движение), энергия частицы может принимать любые значения.
Энергетический спектр свободно движущейся частицы непрерывный.
Для свободной частицы
Из соотношений (3.8) и (3.9) с учетом (3.10) следует дифференциальное уравнение для волновой функции свободно движущейся частицы
Обычно (3.11) записывается в виде
где Δ − оператор Лапласа. Уравнение (3.12) в частных производных называется уравнением движения для свободной частицы. В уравнение движения (3.12) входит только такая характеристика как масса частицы и постоянная Планка ћ. Уравнение (3.12) является дифференциальным уравнением первого порядка по времени. Поэтому для определения волновой функции в произвольный момент времени t достаточно знать значение волновую функцию в начальный момент времени. 3.7. Физические величины и операторы В квантовой механике
постулируется, что каждой физической величине, описываемой в классической
механике в виде функции F(x,y,z,px,py,pz) координат и импульсов ставится в соответствие
линейный оператор
χ(x,y,z,t) = Например, оператор
χ(x,y,z,t) = т. е. Оператор координаты
Для того, чтобы понять почему оператор импульса имеет вид (3.13), воспользуемся тем, что движение свободной частицы описывается уравнением
Оператор кинетической энергии
поэтому операторы
Оператор Гамильтона (гамильтониан) − оператор полной энергии
Если частица движется в потенциальном поле U (x, y, z), то оператор
Гамильтона
Оператор момента количества движения
Оператор квадрата момента количества движения
3.8. Собственные значения и собственные функции операторов С каждым оператором
определяющее его собственные значения Fnи полную систему ортонормированных функций ψn, подчиняющихся определенным граничным условиям. Величины Fn определяют спектр возможных значений физической величины F. Функция ψn(x) характеризует состояние системы, в котором величина F имеет значение Fn. Одно из важнейших положений квантовой теории: в квантовых системах выполняется принцип суперпозиции. Если квантовая система может находиться в состояниях, описываемых функциями ψ1, ψ2, …, ψn, то линейная комбинация (суперпозиция) волновых функций ψ1, ψ2, …, ψn
также является волновой функцией, описывающей одно
из возможных состояний системы, cn – произвольные
постоянные.
где dV = dx dy dz. В частности, средние значения координаты
Средние значения <
Решением уравнений будут волновые функции
где a(y,z),
a(x,z),
a(x,y) –
произвольные функции соответствующих координат (y,z), (x,z), (x,y).
является собственной функцией операторов
A = (2πћ)-3/2. Волновая функция ψp с учетом нормировки имеет вид.
3.9. Коммутация операторов Одним из важных вопросов в квантовой физике является вопрос о том, какие
физические величины могут одновременно иметь определённые значения. Для того
чтобы две величины F и R могли бы иметь определенные значения в некотором
состоянии, описываемом волновой функцией ψn, эта волновая функция,
очевидно, должна быть собственной функцией операторов
Это имеет место только в том случае, когда операторы
Таким образом, если квантовомеханические операторы, соответствующие двум квантовомеханическим величинам, коммутируют, то эти величины могут быть измерены одновременно. Если же операторы не коммутируют, то это величины одновременно не могут иметь определенных значений. Операторы координат и проекции импульса на различные оси коммутируют между собой. Например,
т. е. величины x и py одновременно измеримы.
Поэтому соответствующие им величины xи pxне имеют одновременно
определенных значений.
т. е. квадрат полного момента количества движения и одна из его проекций на произвольную ось могут одновременно иметь определенные значения. 3.10. Статистики Ферми-Дирака и Бозе-Эйнштейна Микрочастицы обладают своеобразной характеристикой, называемой
статистикой. Статистика является проявлением коллективных свойств системы
частиц. Существование статистики является следствием принципа неразличимости
одинаковых микрочастиц и вероятностного характера описания состояний в квантовой
теории.
Поэтому должна быть квантовая характеристика
(квантовое число) и сохраняющаяся физическая величина, отвечающая этому
преобразованию.
Поэтому ε2 =1 и ε = ±1. В релятивистской квантовой теории поля доказывается, что статистика однозначно определяется спином частицы. Частицы с целым (в том числе с нулевым) спином называются бозонами и подчиняются статистике Бозе-Эйнштейна (γ‑кванты, π-мезоны, α-частицы и др.). Частицы с полуцелым спином называются фермионами и подчиняются статистике Ферми-Дирака (электроны, кварки, нейтрино, протоны, нейтроны, ядра с нечётным числом нуклонов и т.д.).
3.11. Принцип Паули для тождественных фермионов.Для системы тождественных фермионов ψ(2,1,...,A) = −ψ(1,2,...,A). Пусть частицы 1 и 2 находятся в одинаковом состоянии. Тогда
ψ(2,1,...,A) и ψ(1,2,...,A) одна и та же функция и
ψ = -ψ, 2ψ = 0, ψ = 0, т. е. такого состояния нет. Таким образом, в системах,
подчиняющихся статистике Ферми-Дирака и описываемых антисимметричными
волновыми функциями, не должно существовать двух тождественных частиц с
полностью совпадающими характеристиками. Поясним различие между тремя
статистиками – классической, статистикой Ферми-Дирака и статистикой Бозе-Эйнштейна – на простейшем случае, когда имеются две одинаковых частицы и
два различных одночастичных состояния. Число возможных состояний такой
физической системы будет разным для разных статистик. Структура электронных оболочек в атоме и нуклонных оболочек в ядре объясняется на основе принципа Паули. В атоме два электрона не могут находиться в одинаковом состоянии. Точно так же и в ядре два одинаковых нуклона не могут находиться в одном и том же состоянии. Принципу Паули подчиняются только фермионы.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
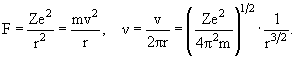
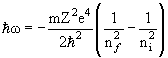
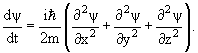
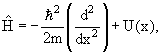 0 ≤ x ≤ L
0 ≤ x ≤ L