Масса и энергия связи ядра

    Масса ядра измеряется в атомных единицах массы (а.е.м). За одну атомную единицу массы принимается 1/12 часть массы нейтрального атома углерода ¹² С:

1а.е.м = 1.6606 10^-27 кг.

А.е.м. выражается через энергетические единицы:

1а.е.м = 1.510^-3 эрг = 1.510^-10Дж = 931.49 МэВ

Масса ядра всегда меньше суммы масс составляющих его нуклонов.

    Избыток масс Δ связан с массой атома M_ат(A,Z) и массовым числом A соотношением:

Δ = М_ат(A,Z) - А.

    Энергия связи ядра E_св(A,Z) это минимальная энергия, необходимая, чтобы развалить ядро на отдельные, составляющие его нуклоны.

Е_св(A, Z) = [Z m_p + (A - Z)m_n - M(A, Z)]c²,

где Z - число протонов, ( A - Z) - число нейтронов, m_p - масса протона, m_n - масса нейтрона, М(A,Z) - масса ядра с массовым числом А и зарядом Z.
Энергия связи ядра, выраженная через массу атома M_ат, имеет вид:

Е_св(A, Z) = [Zm_H + (A - Z)m_n - M_ат(A, Z)]c² ,

где m_H - масса атома водорода.

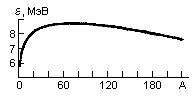
    Удельная энергия связи ядра ε(A, Z) это энергия связи, приходящаяся на один нуклон

ε(A, Z) = E_св(A,Z) / A.

    На рис. 1 показана зависимость удельной энергии связи ядра ε от числа нуклонов A. Видно, что наиболее сильно связаны ядра в районе железа и никеля (A ~ 55-60). Такой ход зависимости ε(A) показывает, что для легких ядер энергетически выгодны реакции синтеза более тяжелых ядер, а тяжелых − деление на более легкие осколки.

    Используется также понятие энергия связи (отделения) частицы в ядре

    Энергия отделения нейтрона

B_n = [М(А-1,Z) + m_n − М(А, Z)]c² = W(А, Z) − W(А-1,Z).

    Энергия отделения протона

B_p = [М(А-1,Z-1) + m_p − М(А, Z)]c² = W(А, Z) − W(А-1,Z-1).

    Энергия отделения α-частицы

B_α = [M(A-4,Z-2) + m_α − M(A,Z)]c² = W(A,Z) − W(A-4,Z-2) − W(4,2).

    Наиболее устойчивы ядра, у которых магическое число протонов или нейтронов.

17.11.15