6. Ширина и структура гигантского резонанса "Ширина" и "структура" - основные понятия,
характеризующие общую форму сечений фотопоглощения (или фотонуклонных реакций) и
детали этой формы. Мы постепенно введем читателя в содержание этих понятий, а
пока подчеркнем их важность в качестве жесткого теста справедливости различных
теоретических подходов к описанию ГДР. Если теория в состоянии дать хорошее
количественное описание ширины и структуры ГДР, а также характеристик его
распада, - прежде всего спектров фотонуклонов, - то можно говорить о достаточно
полном понимании процесса формирования и релаксации гигантского дипольного
резонанса. Пока эта задача до конца не решена, хотя в концептуальном плане ясно,
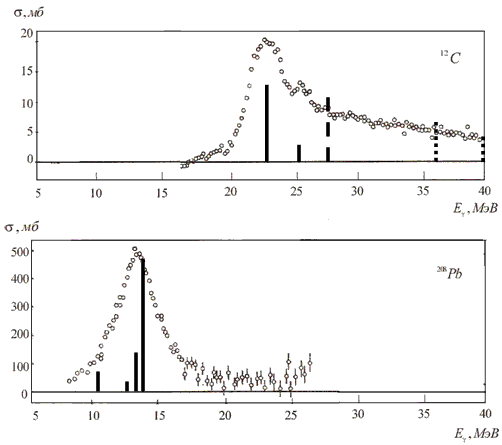
что нужно учесть для её решения. Рис. 26. Сечения поглощения фотонов ядрами 12С и 208Рb. Экспериментальные данные [41] взяты из работ [32] и [33] соответственно. Столбики - Е1-переходы, полученные в многочастичной модели оболочек [34] и [18]. Для 12С сплошные столбики относятся к переходам, в которых доминирующая роль принадлежит нуклонам подоболочки 1p3/2, пунктир - подоболочки 1p1/2, точки - оболочки 1s1/2 Растаскивание дипольной силы
Е1-переходов по большому энергетическому интервалу, которое имеет место в легких
ядрах и возникает за счет сильных различий в энергиях нуклонных оболочек,
называют конфигурационным расщеплением гигантского резонанса. Это явление
мы подробно рассмотрим в §8. Возвращаясь к 12С, отметим, что для
этого ядра конфигурационное расщепление ГДР возникает как расщепление между
переходами из 1р-оболочки (сплошные столбики и пунктир) и 1s-оболочки (точечные
столбики). Волновая функция каждого из этих возбуждений и после учета
остаточного взаимодействия сохраняет свою одночастичную природу, т.е.
формируется, по существу, одним (на 73-99% [34])
частично-дырочным переходом. На примере 12С видно, что
конфигурационное расщепление может формировать наиболее масштабную структуру
сечений ядерного фоторасщепления. Такую структуру называют гросс-структурой
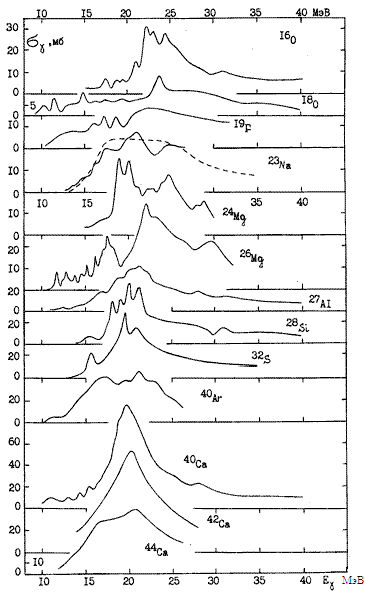
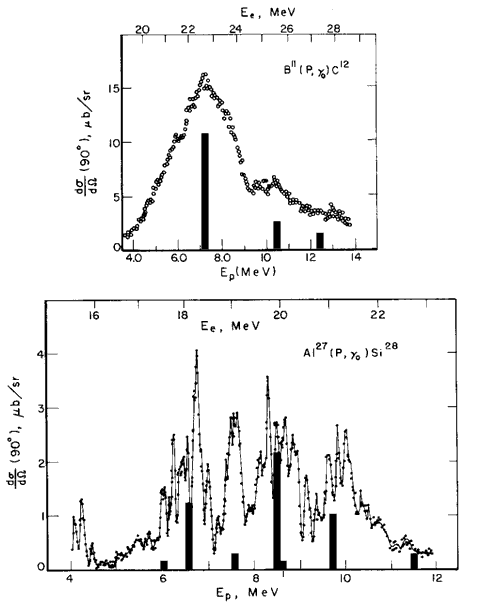
ГДР. Рис. 27.Сводка экспериментальных сечений фотопоглощения ядер 1d2s-оболочки (16 < А < 44) Помимо гросс-структуры и промежуточной структуры форма гигантского резонанса может характеризоваться и более мелкими деталями, которые называют тонкой структурой ГДР. Приведем пример такой структуры. Для этого рассмотрим рис. 28, на котором приведены сечения реакций 11В(p,γ0)12С и 27Al(p,γ0)28Si, с заселением основных состояний конечных ядер. Рис. 28. Сечения реакций 11В(p,γ0)12С [35] и 27Al(p,γ0)28Si [36] и данные теоретических расчетов фоторасщепления в рамках многочастичной модели оболочек [31, 34, 66]. Шкала энергий возбуждения ядер 12С и 28Si дана сверху Реакции (p,γ0) весьма удобны
для исследования тонких деталей формы фотоядерных сечений в силу их чрезвычайно
высокого энергетического разрешения, достигающего 10 кэВ. Дифференциальные
сечения
где JA и JB - спины ядер А и В, а
где Bp - энергия отделения протона из ядра А. Таким образом,
измеряя сечения реакций (p,γ0), можно получить данные о сечениях
реакций (γ,p0) с энергетическим разрешением, не доступным в прямых
фотоядерных экспериментах.
Сравнение полученных цифр с тем, что изображено на рис. 23 приводит к
ассоциированию резонансов тонкой структуры с состояниями типа 2p2h (две частицы
- две дырки). То, что резонансы промежуточной структуры гигантского резонанса
ядра 28Si, представленные на рис. 28, обусловлены распадом ГДР этого
ядра на стадии входных 1p1h-состояний, достаточно убедительно подтверждается и
спектром этих состояний, рассчитанном в многочастичной модели оболочек [31]
и показанном столбиками.
где
Подчеркнём, что выражение (73) применимо к отдельному дипольному состоянию, а не к гигантскому резонансу в целом. Г↑ обычно получают в оболочечных расчетах с учетом волновой функции дипольного 1p1h-состояния и проницаемости кулоновского и центробежного барьеров. При этом Г↑ может меняться примерно от 0.2 МэВ до нескольких МэВ, имея тенденцию уменьшаться с ростом массового числа А. Для наиболее сильных дипольных состояний чаще всего Г↑ ≈ 0.5-2 МэВ. В обсуждаемом случае ядра 12С эта величина ≈ 3 МэВ и в районе максимума ГДР вероятность полупрямого распада Г↑/Г ≈ 1.
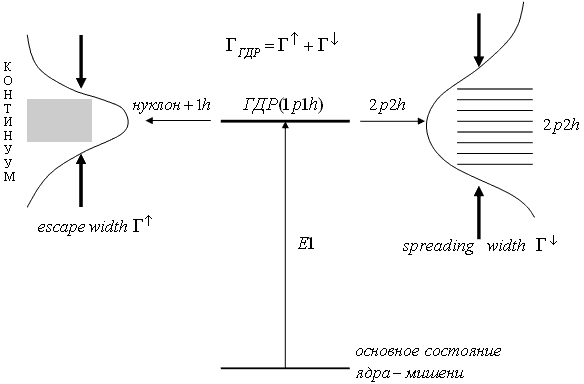
Рис. 29. Пояснение к процессу формирования ширины гигантского резонанса. Под ГДР в данном случае понимается одно когерентное дипольное состояние Ширину Г↑ называют шириной эмиссии или
вылета (английский термин escape width), а ширину Г↓ - шириной
разброса (дипольного состояния). Английские эквиваленты последней - spreading
width, реже damping width. Подобная терминология для Г↓ объясняется
тем, что процесс 1p1h→2p2h приводит к дроблению дипольного состояния на более
мелкие резонансы и "растаскиванию"
их по энергетической области с характерной шириной Г↓. Каждый из этих
мелких 2p2h-резонансов в этом процессе не приобретает собственной ширины.
Собственная ширина у них появляется лишь в результате дальнейшей эмиссии нуклона
из этих 2p2h-состояний. Очевидно, ширина Г↑ имеет более привычный
смысл - это ширина на половине высоты плавной резонансной кривой с
брейт-вигнеровской энергетической зависимостью. Рис. 29 поясняет сказанное.
Из табл. 6 видно, что ρ2p2h быстро
растет с ростом А. Кроме того, ρ2p2h быстро увеличивается и с ростом
энергии возбуждения. Полное число 2p2h-состояний в области гигантского
резонанса у массивных ядер огромно. Так у ядра 208Pb полное число
2p2h-состояний с JP
= 1- в области энергий от 5 до 20 МэВ приближается к 35 000 [37].
Столь значительные ρ2p2h, даже при относительно небольших величинах
среднеквадратичных матричных элементов
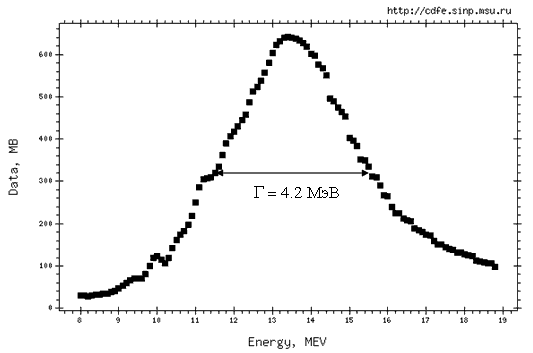
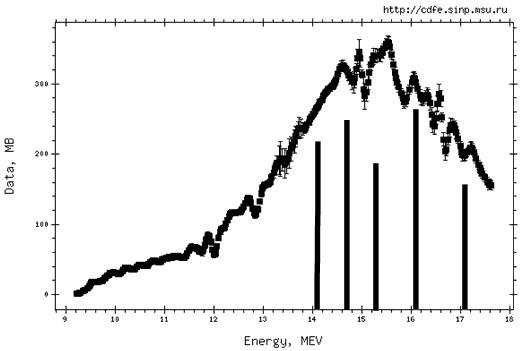
Рис. 30. Оцененное по всем экспериментальным данным сечение фотопоглощения для ядра 208Pb [41] Для более легких ядер соотношение Г↓ и Г↑ можно получить из экспериментальных данных различного типа. Назовем два основных сорта подобных экспериментальных данных. Во-первых, это спектры и угловые распределения фотонуклонов. Если нуклонные спектры имеют испарительный характер, то ядра достигают стадии теплового равновесия, т.е. полупрямому распаду (1p1h → нуклон + 1h) они "предпочитают" распад 1p1h → 2p2h. При этом угловые распределения фотонуклонов должны быть преимущественно изотропными. Во-вторых, это фиксация уровней конечных А-1 ядер, которые заселяются при нуклонном распаде исходного ядра, содержащего А нуклонов. При этом определяется вероятность, с которой заселяются отдельные конечные состояния. Знание частично-дырочной природы этих конечных состояний относительно основного состояния ядра-мишени, т.е. принадлежности их, например, к состояниям типа 1h, 1p2h, 2p3h или ещё более сложным, позволяет сразу установить на какой стадии ядерной релаксации произошёл вылет нуклона, и тем самым определить механизм распада дипольного состояния, который предшествовал этому вылету (см. рис. 23). Только что описанный второй способ установления механизма фотонуклонной реакции является идеологически более обоснованным и надежным, хотя методически существенно более сложным. Более детально мы его опишем в §8, а в данном параграфе мы лишь воспользуемся результатами этого метода.
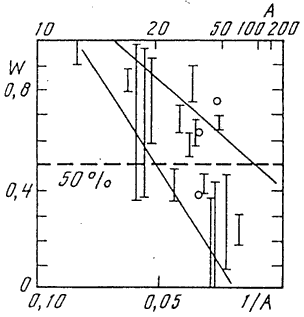
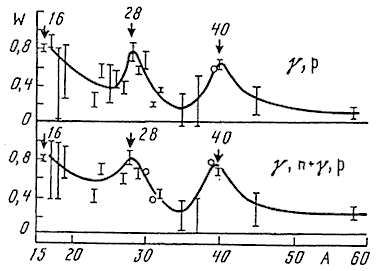
Рис. 31. Сводка данных о вероятностях W полупрямого распада гигантского резонанса в области массовых чисел 12-58 [42] Рассмотрим теперь общую ситуацию с ядрами более лёгкими, чем 208Pb. Обратимся к рис. 31, на котором дана сводка [42] наиболее надежных данных о вероятностях полупрямого распада гигантского резонанса ядер с А = 12-58, извлеченных из фотонуклонных реакций с заселением отдельных уровней конечных ядер (второй метод установления механизма фотоядерной реакции). Из этих данных видно, что в легких ядрах (А < 40) доминирует полупрямой распад гигантского резонанса. Вероятность полупрямого распада максимальна в самых легких ядрах (А < 12), где она достигает 100%. С ростом А доля полупрямого распада уменьшается и у ядер тяжелее дважды магического 40Са основной формой распада дипольного состояния становится переход к более сложным внутриядерным возбуждениям (1p1h → 2p2h). Рис. 31 предсказывает для самых тяжелых ядер долю полупрямых распадов в районе 10%, что согласуется с вышеприведенными нами оценками на основе ширины гигантского резонанса ядра 208Pb.
Рис. 32. Вероятности W полупрямых процессов в фотопротонном сечении (верхний рисунок) и полном фотонуклонном сечении (нижний рисунок) для ядер с А = 12-58 [42] Рис. 31 хорошо демонстрирует общую
тенденцию падения вероятности полупрямого распада ГДР с ростом числа нуклонов в
ядре. Но на фоне этой общей тенденции наблюдаются области повышенной и
пониженной вероятности, что видно из более детального рис. 32. Характерно, что
доля полупрямых процессов имеет локальные максимумы для магических ядер 16О
и 40Са и полумагического ядра 28Si. Именно у таких ядер (с
замкнутыми оболочками) плотность 2p2h-состояний с JP = 1- и
T = 1 в области энергий гигантского резонанса, минимальна, т.е. минимальна Г↓ и
соответственно возрастает Г↑.
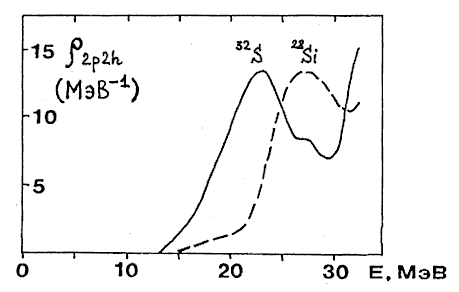
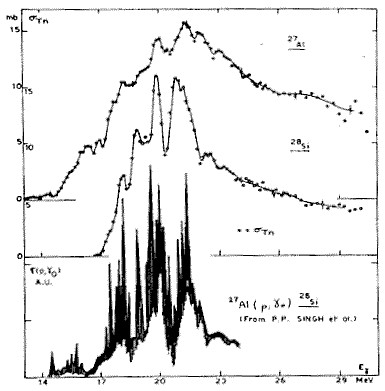
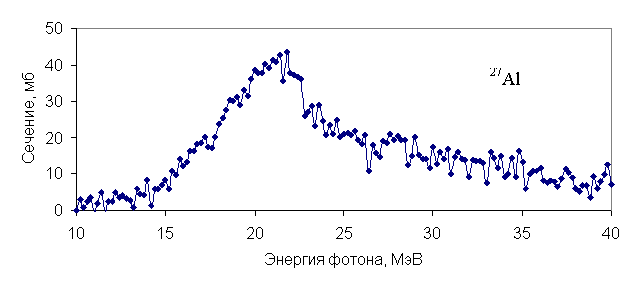
Рис. 33. Плотности ρ2p2h состояний 2p2h, на которые могут распадаться дипольные состояния в ядрах 28Si и 32S [31] Другая показательная в этом отношении пара ядер 27Al и 28Si. Ядро 27Al имеет всего лишь на один нуклон меньше, чем 28Si, а вероятность полупрямого распада ГДР у него существенно ниже - 55-60% против 80% у 28Si. Особенно сильное уменьшение вероятности полупрямого распада (до 30-40%) наблюдается в доминирующем для 27Al фотопротонном канале. Подобное резкое уменьшение вероятности полупрямого распада ГДР у 27Al можно объяснить сильным возрастанием у этого ядра плотности ρ2p2h состояний 2p2h в области энергий ГДР. Расчетов этой плотности не проводилось, но и без этих расчетов ясно, что наличие нечетного нуклона у нечетно-четного ядра 27Al должно привести к существенному возрастанию ρ2p2h в этом ядре по сравнению с четно-четным ядром 28Si. Одним из следствий этого должно быть заметное смягчение фотопротонных спектров у 27Al по сравнению с 28Si. Как показали эксперименты [43, 44] это действительно имеет место. Однако, на наш взгляд, более показательным эффектом, который должен наблюдаться в этом случае (при резком возрастании ρ2p2h для 27Al), является эффект "заглаживания" промежуточной структуры фотоядерных сечений для этого ядра. Для того, чтобы проверить это, нужно сравнить одни и те же фотоядерные сечения двух обсуждаемых ядер, измеренные в максимально идентичных условиях. В этом случае найденные отличия в характере структуры сечений можно целиком отнести за счёт отличия в механизме фотоядерной реакции у сравниваемых ядер. Для заявленного анализа идеально подходят фотонейтронные сечения на 27Al и 28Si, измеренные фотоядерной группой Саклэ (Франция) на пучке квазимонохроматических аннигилляционных фотонов [45]. Измерения выполнялись на одной и той же установке в одной и той же экспериментальной сессии. Данные этого эксперимента приведены на рис. 34. Рис. 34. Сравнение сечений фотонейтронных реакций для 27Al и 28Si, измеренных в одинаковых условиях [45] (два верхних сечения). На нижнем рисунке приведено прецизионное сечение реакции 27Al(p,γ0)28Si [36] Из рис. 34 хорошо видно, что ярко выраженная промежуточная структура гигантского резонанса ядра 28Si, состоящая из четырех пиков в фотонейтроном сечении в области 18-22 МэВ, почти полностью исчезает в сечении фотонейтронной реакции ядра 27Al. Это "заглаживание" структуры сечения в случае 27Al можно объяснить сильным увеличением плотности 2p2h-состояний в 27Al по сравнению с 28Si. Более плотный фон 2p2h-состояний увеличивает ширину разброса Г↓ резонанса промежуточной структуры согласно выражению (72) и приводит к распределению вероятности Е1-перехода каждого из этих 1p1h-резонансов по состояниям более сложной природы, распределенным в существенно более широком энергетическом интервале. Резонансы промежуточной структуры, наблюдающиеся в сечении реакции 28Si(γ,n), это те же резонансы, которые видны в сечении реакции 27Al(p,γ0)28Si [36], характеризующимся более высоким энергетическим разрешением (нижняя часть рис. 34). Детали этого последнего сечения лучше видны на обсуждавшемся нами ранее рис. 28.
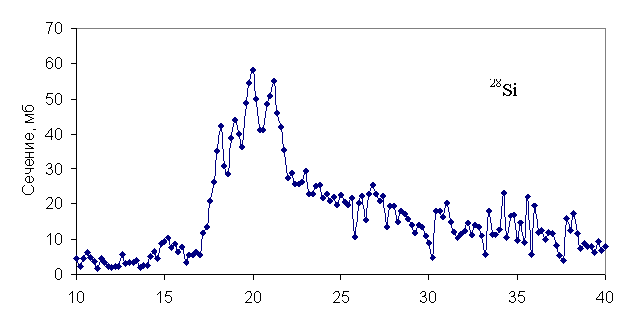
Рис. 35. Сечения фотопоглощения на ядрах 27Al и 28Si, измеренные в одном эксперименте [32] Эффект исчезновения промежуточной
структуры в гигантском резонансе при переходе от ядра 28Si к ядру
27Al не менее убедительно проявляется и в сечениях фотопоглощения этих
ядер, измеренных с высокой точностью в одном и том же эксперименте в Майнце
(Германия) [32].
Эти сечения показаны на рис. 35 и после всего, что было сказано нами до этого,
они не требуют дополнительных комментариев.
Это в основном вытянутые ядра и параметр деформации β для них достигает
значений ≈0.35 (см. рис. 12). Рис.
8, 10,
11 и 12 и
табл. 3 достаточно полно демонстрируют характер
влияния деформации на характеристики ГДР. На "краях" вышеперечисленных зон
деформации ядра близки к магическим и имеют сферическую или почти сферическую
форму. Сечения фотопоглощения таких ядер с хорошей точностью представляют собой
одиночный гладкий резонанс (одно дипольное состояние) с шириной Г0 ≈ 4
МэВ (см. приведенное на рис. 8 сечение для 142Nd,
имеющего магическое число нейтронов 82, и сечение для дважды магического ядра
208Рb, приведенное на рис. 30). По мере увеличения степени деформации β
ширина ГДР растет примерно как Г = Г0 + ΔГ, где ΔГ ≈ 12β МэВ,
достигая значения ≈ 8 МэВ. При большой деформации (β ≈ 0,3) связанное с ней
расщепление ГДР проявляется явно в виде хорошо разрешенных двух максимумов (рис.
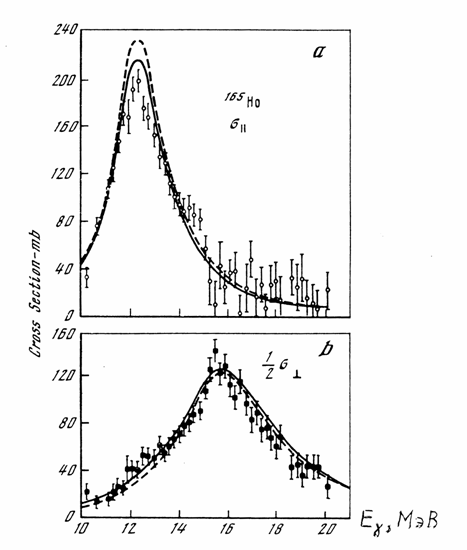
8, 10), т.е. двух раздвинутых дипольных состояний. Рис. 36. Результаты декомпозиции сечения фотопоглощения ядра
165Но на парциальные компоненты, отвечающие Е1-колебаниям вдоль (σ||)
и перпендикулярно ( В только что рассмотренных массивных деформированных ядрах сечения фотопоглощения хорошо аппроксимируются двумя гладкими резонансными кривыми, раздвинутыми за счет разности частот Е1-колебаний вдоль короткой и длинной осей ядерного эллипсоида. По существу этим и определяется результирующая форма сечения фотопоглощения таких ядер. Никакой выраженной промежуточной структуры ГДР в таких ядрах не наблюдают. Она "заглажена" взаимодействием входных когерентных 1p1h-состояний с плотным фоном некогерентных (неколлективизированных) 2p2h-состояний. К этому вопросу отсутствия промежуточной структуры ГДР у массивных деформированных ядер (и тяжелого сферического ядра 208Pb) мы ещё вернемся ниже в данном параграфе, а сейчас обратимся к средним и тяжелым ядрам, у которых промежуточная структура гигантского резонанса проявляется. Примерами таких ядер являются ядра 141Pr и 60Ni. Их сечения фотопоглощения показаны на рис. 37 и 38. Оба ядра являются сферическими (или почти сферическими). Спектр их нижних состояний вибрационный, т.е. формируется квадрупольными колебаниями поверхности ядра. Более того, амплитуда таких колебаний сравнительно велика. Подобные ядра относят к так называемым мягким вибрационным ядрам, поверхность которых очень пластична, т.е. легко поддается изменению. Естественно связать появление промежуточной структуры ГДР таких ядер с податливостью их поверхности к изменению формы. Учет связи высокоэнергичных (15-20 МэВ) поляризационных дипольных колебаний ядерной плотности с низкоэнергичными (≈ 1 МэВ) квадрупольными колебаниями поверхности ядра проще всего осуществить в рамках так называемой коллективной динамической модели (КДМ). В этой модели оба типа колебаний рассматриваются как сугубо коллективные. Описание КДМ и ссылки на оригинальные работы можно найти в монографии [46]. Гамильтониан модели имеет следующий вид
где первые два слагаемых описывают независимые коллективные дипольные и квадрупольные колебания, а последний - взаимодействие между ними. Учет этого взаимодействия неизбежно приводит к структуре ГДР. Это легко понять, поскольку быстрые Е1-колебания разворачиваются на фоне медленно меняющейся ядерной поверхности, которая, потеряв свою сферичность, меняет со временем степень своей деформированности. Поэтому итоговый спектр Е1-колебаний эффективно возникает как набор гигантских резонансов ядер с различными деформациями. Параметрами модели являются энергия ћω2 квадрупольного фонона (энергия первого возбужденного 2+-уровня в четно-четном ядре), β2 - среднеквадратичная динамическая квадрупольная деформация (амплитуда квадрупольных колебаний) и число N квадрупольных фононов. Чем меньше ћω2, больше β2 и N, тем сильнее разброс Е1-резонанса и богаче его промежуточная структура. На рис. 37 приводится оцененное по всем экспериментальным данным сечение реакции 141Pr(γ,n) [47], которое фактически является сечением фотопоглощения для этого ядра, и данные расчета в рамках коллективной динамической модели c параметрами низкоэнергичного спектра соседнего четно-четного ядра 146Nd. Без учета взаимодействия дипольных и квадрупольных степеней свободы гигантский резонанс ядра 141Pr в данном сугубо коллективном подходе представлял бы собой всего лишь одну резонансную линию. Без учета процессов диссипации этого дипольного возбуждения, вызванного взаимодействием с поверхностью ядра, ширина ГДР ядра 141Pr давалась бы только шириной нуклонной эмиссии Г↑, которая для столь массивного ядра слишком мала (0.5-1 МэВ), что бы объяснить наблюдаемую ширину сечения фотопоглощения. Как видно из рис.37, включение диполь-квадрупольного трения рассыпает дипольное возбуждение по пяти близким по интесивности переходам, располагающимся в энергетическом интервале ≈ 3 МэВ, что и позволяет, по крайней мере, качественно, воспроизвести экспериментальную ширину сечения фотопоглощения ядра 141Pr. Рис. 37. Сечение реакции 141Pr(γ,n) [47] (точки) и данные расчета (столбики) спектра Е1-переходов в рамках коллективной динамической модели с параметрами низкоэнергичного спектра ядра 146Nd С точки зрения частично-дырочной терминологии
учёт в коллективной динамической модели взаимодействия дипольных и квадрупольных
колебаний соответствует учету переходов 1p1h→2p2h. Очевидно, из-за очень высокой
плотности 2p2h-состояний в массивных ядрах произвести полный учет
таких переходов невозможно. Однако, если удастся сформулировать физически
обоснованный принцип отбора наиболее важных переходов 1p1h→2p2h, то есть надежда
резко сократить число 2p2h-состояний, реально влияющих на рассматриваемый
процесс, и все их учесть. Такой принцип и предлагает КДМ. Он состоит в учете
только таких 2p2h-состояний, которые включают коллективные возбуждения.
Напомним, что с точки зрения микроскопического подхода любое коллективное
возбуждение (т.е. фонон) есть когерентное, т.е. коллективизированное
1p1h-состояние. Электрический дипольный фонон это когерентное 1p1h-состояние с JP = 1- и
Т = 1 (в чётно-чётном ядре). Электрический квадрупольный фонон это когерентное
1p1h-состояние с JP = 2+ и Т = 0 и т.д. Двухфононное
состояние (фонон + фонон) это суперпозиция двух когерентных 1p1h-состояний либо
одного и того же типа (например, двух электрических дипольных фононов или двух
электрических квадрупольных фононов), либо фононов разного типа (например, 1
дипольный фонон + 1 квадрупольный фонон). В коллективной динамической модели
учтены лишь такие процессы 1p1h→2p2h, которые отвечают переходам "1 дипольный
фонон → 1 дипольный фонон + 1 квадрупольный фонон". В расчетах по КДМ учитывают
и последующие стадии ядерной релаксации 2p2h→3p3h→… путем простого
увеличения числа квадрупольных фононов (иногда до 8). Таким образом, в подобном
подходе удается, во-первых, резко ограничив пространство 2p2h-состояний
состояниями типа фонон + фонон, все их учесть и, во-вторых, ассоциировать
промежуточную структуру сечений фотопоглощения именно с такими состояниями.
Вопрос о том, насколько данная модель в состоянии описать структуру гигантского
резонанса средних и тяжелых ядер, до сих пор открыт. Ясно, что какая-то часть
структуры и ширины этих сечений особенно у вибрационных ядер в принципе может
быть описана в таком подходе. Все проведенные до сих пор расчеты в КДМ на наш
взгляд являются лишь качественной иллюстрацией одного из возможных (хотя и
довольно вероятных) механизмов формирования ширины и структуры гигантского
резонанса средних и тяжелых ядер.
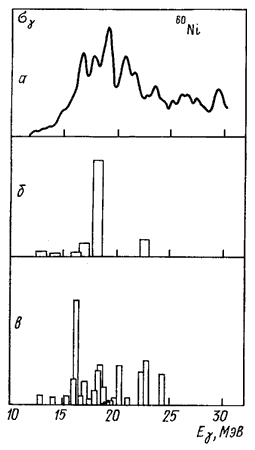
где Hph описывает Е1-возбуждения в рамках 1p1h-формализма модели оболочек, а Hквадр- квадрупольные колебания поверхности ядра на языке коллективной модели. Взаимодействие этих двух степеней свободы описывается гамильтонианом Hph-квадр. Пример подобного расчета для ядра 60Ni [48] приведен на рис. 38в. Результат стандартного расчета в рамках 1p1h-приближения модели оболочек для этого ядра [50] приведен на рис. 38б. Экспериментальное сечение фотопоглощения [49] показано на рис. 38а. Рис. 38. Гигантский дипольный резонанс ядра 60Ni. а - экспериментальное сечение фотопоглощения [49], б - расчет в рамках 1p1h-приближения модели оболочек [50], в - расчет в модели коллективных корреляций [48] Из рис. 38 видно, что промежуточная структура гигантского резонанса ядра 60Ni в принципе может быть интерпретирована как проявление "коллективных корреляций", т.е. как структура, возникающая за счет взаимодействия дипольных 1p1h-возбуждений с квадрупольными колебаниями поверхности ядра. 24.04.2014 |
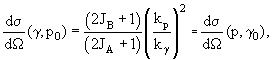
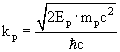 и
kγ = Eγ/ћc - волновые числа протона и нейтрона, причем
энергия возбуждения Eexc ядра А связана с кинетической энергией
протона Ep соотношением
и
kγ = Eγ/ћc - волновые числа протона и нейтрона, причем
энергия возбуждения Eexc ядра А связана с кинетической энергией
протона Ep соотношением