2.3. Комплексные числа
Рассмотрим элементы вида z = x + yi,
где x и y - действительные числа, а i -
некоторый элемент, называемый мнимой единицей
(см. *).
Элемент z = x + yi
называют комплексным числом, x - его действительной,
а y - мнимой частью и пишут
x = Re z, y = Im z.
(От латинских слов realus - действительный,
imaginarius - мнимый)
Два комплексных числа считаются
равными тогда и только тогда, когда равны их
действительные и мнимые части.
Вместо x + 0i и 0 + yi
пишут соответственно x и yi, в частности,
0 + 0i = 0; вместо 1i пишут i.
Число x + yi, у которого y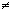 0, называют существенно
комплексным числом, а число вида yi, y
0, называют существенно
комплексным числом, а число вида yi, y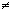 0, - чисто мнимым.
0, - чисто мнимым.
Множество всех комплексных чисел
обозначают через C.
Арифметические операции. С помощью
операций сложения и умножения действительных
чисел в множестве комплексных чисел также можно
ввести операции сложения и умножения.
Для комплексных чисел z1 = x1 + y1i
и z2 = x2 + y2i
их сумма z1 + z2
определяется как комплексное число,
действительная и мнимая части которого
получаются в результате сложения соответственно
действительных и мнимых частей чисел z1
и z2:
z1 + z2 (x1 + x2)
+ (y1 + y2)i.
(x1 + x2)
+ (y1 + y2)i.
Для определения произведения
комплексных чисел сначала определим квадрат
мнимой единицы:
i2 ii
ii -1,
-1,
а затем - произведение двух произвольных
комплексных чисел z1 = x1 + y1i
и z2 = x2 + y2i
как результат почленного умножения z1 = x1 + y1i
на z2 = x2 + y2i
с использованием соотношения i2 = -1
и последующего сложения полученных результатов:
z1z2 =
(x1 + y1i)(x2 + y2i)
 x1x2
+ y1x2i + x1 y2i
+ y1 y2i2 = (x1x2 - y1 y2)
+ (x1 y2+x2 y1)i. x1x2
+ y1x2i + x1 y2i
+ y1 y2i2 = (x1x2 - y1 y2)
+ (x1 y2+x2 y1)i. |
(2.3) |
Замечание. При определении умножения
комплексных чисел можно было бы предварительно
не определять, что i2 = -1, и не
использовать правила почленного умножения, а
сразу определить произведение по формуле (2.3).
Тогда из нее бы уже следовало, что i2 = -1.
В самом деле,
ii = (0 + 1 i)(0 + 1 i)(0 + 1 i) i) |
= |
-1. |
|
(2.3) |
|
Вычитание определяется как действие,
обратное сложению: z = z1 - z2,
если z1 = z2 + z, а деление -
как действие, обратное умножению: z = z1/z2,
z2 0, если z1 = z2z.
0, если z1 = z2z.
Определенные указанным образом
арифметические операции над комплексными
числами удовлетворяют группам аксиом I, II, III, п. 2.1. Теперь можно
сформулировать более полное и более точное
определение множества комплексных чисел C.
Определение 2. Множество всех
элементов x + yi, в котором заданы
операции сложения, вычитания, умножения и
деления согласно выше сформулированным
правилам, называется множеством комплексных
чисел, а каждый его элемент - комплексным
числом.
Обозначение x + yi
комплексных чисел называется их алгебраической
формой записи.
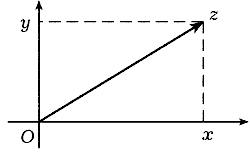
Рис. 7
|
Векторная интерпретация. Каждому
комплексному числу z = x + yi
соответствует упорядоченная пара
действительных чисел (x, y), и
наоборот, каждой упорядоченной паре
действительных чисел (x, y)
соответствует комплексное число z = x + yi,
и эти соответствия взаимно однозначны. С
упорядоченными же парами действительных чисел (x, y)
на плоскости (при фиксированной системе
декартовых координат) находятся во взаимно
однозначном соответствии векторы этой плоскости
имеющие числа x и y своими координатами. В
результате комплексное число z = x + yi
можно рассматривать как вектор на плоскости с
координатами x,y. Этот вектор мы будем
обозначать той же буквой z = (x,y)
(рис. 7).
Целесообразность такой
интерпретации комплексных чисел следует из того,
что при сложении комплексных чисел складываются
и соответствующие им векторы: при сложении
векторов их координаты складываются, поэтому
суммой векторов z1 = (x1, y1)
и z2 = (x2, y2)
является вектор
z1 + z2 = (x1 + x2,
y1 + y2),
т. е. вектор, соответствующий сумме z1 + z2
комплексных чисел z1 = x1 + y1i
и z2 = x2 + y2i
(рис. 8).
Поскольку вычитание как для
комплексных чисел, так и для векторов является
действием, обратным сложению, то при вычитании
комплексных чисел соответствующие им векторы
также вычитаются (рис. 9).
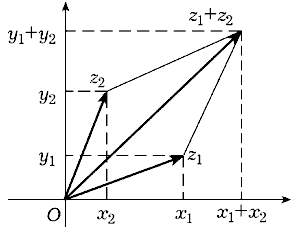
Рис. 8 |
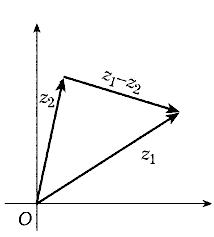
Рис. 9 |
Координатная
плоскость, векторы z = (x,y) которой
интерпретируются как комплексные числа,
называется комплексной плоскостью, ее ось x -
действительной осью, а ось y - мнимой.
Длина |z| вектора z = (x,y)
называется модулем или абсолютной
величиной комплексного числа z = x + yi.
Очевидно,

|
(2.4) |
Поскольку длина каждой стороны
треугольника не превосходит суммы длин двух
других его сторон, а абсолютная величина
разности длин двух сторон треугольника не меньше
длины третьей стороны, то для любых двух
комплексных чисел z1 и z2
имеют место неравенства (см. рис. 8 и рис. 9)
|z1 + z2| <
|z1| + |z2|,
||z1| - |z2|| < |z1
- z2|. |
(2.5) |
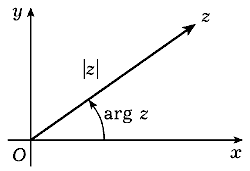
Рис. 10
|
Аргумент комплексного числа.
Если  - угол,
образованный ненулевым вектором z с
действительной осью, то всякий угол вида
- угол,
образованный ненулевым вектором z с
действительной осью, то всякий угол вида
 + 2
+ 2 n,
где n - целое число, и угол только такого
вида, также будет углом, образованным вектором z
с действительной осью.
n,
где n - целое число, и угол только такого
вида, также будет углом, образованным вектором z
с действительной осью.
Множество всех углов, которые образует
ненулевой вектор z = (x,y) с
действительной осью, называется аргументом
комплексного числа z = x + yi
и обозначается arg z. Каждый элемент этого
множества называется значением аргумента
числа arg z (рис. 10).
Часто для краткости вместо
"значение аргумента" говорят
"аргумент" и обозначают его тем же символом
arg z, что и все множество (подобно тому, как в
теории неопределенных интегралов множество всех
первообразных данной функции f обозначается
тем же символом 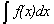 , что и
произвольный элемент этого множества; см. п. 28.1).
, что и
произвольный элемент этого множества; см. п. 28.1).
Поскольку ненулевой вектор плоскости
однозначно определяется своей длиной и углом,
который он образует с осью x, то два
комплексных числа, отличные от нуля, равны тогда
и только тогда, когда равны их абсолютные
величины и аргументы.
Если на значения аргумента  числа
числа  наложить, например, условие 0 <
наложить, например, условие 0 <  < 2
< 2 или условие
-
или условие
- <
<  <
<
 , то значение аргумента будет
определено однозначно. Это ограничение, однако,
как мы в этом убедимся в дальнейшем, не всегда
удобно. Из определения аргумента следует, что tg
, то значение аргумента будет
определено однозначно. Это ограничение, однако,
как мы в этом убедимся в дальнейшем, не всегда
удобно. Из определения аргумента следует, что tg  = y/x. Здесь при x = 0,
y
= y/x. Здесь при x = 0,
y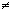 0 считается y/0
=
0 считается y/0
= 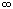 .
.
Тригонометрическая форма
записи комплексного числа. Действительная и
мнимая части комплексного числа z = x + yi 0 выражаются через его
модуль r = |z| и аргумент
0 выражаются через его
модуль r = |z| и аргумент  следующим образом:
следующим образом:
x = r cos  , y = r sin , y = r sin  . . |
(2.6) |
Отсюда
z = x + yi
= r (cos  + isin + isin  ). ). |
(2.7) |
Правая часть этого равенства
называется тригонометрической формой записи
комплексного числа z. Мы будем ее
употреблять и для z = 0; в этом случае r = 0,
а  может принимать
любое значение - аргумент числа 0 не
определен. Итак, всякое комплексное число можно
записать в тригонометрической форме.
может принимать
любое значение - аргумент числа 0 не
определен. Итак, всякое комплексное число можно
записать в тригонометрической форме.
Ясно также, что если комплексное число z
записано в виде
r (cos  + isin
+ isin
 ), r > 0,
), r > 0,
то число r является его модулем (ибо  ), а
), а  - одним из значений его аргумента.
- одним из значений его аргумента.
Запись операций умножения, деления и
возведения в степень в тригонометрической форме.
Тригонометрическую форму записи комплексных
чисел бывает удобно использовать при
перемножении комплексных чисел, в частности, она
позволяет выяснить геометрический смысл
произведения комплексных чисел.
Найдем формулы для умножения и деления
комплексных чисел при тригонометрической форме
их записи. Если
z1 = r1 (cos  1 + isin
1 + isin  1), z2 = r2
(cos
1), z2 = r2
(cos  2 + isin
2 + isin  2),
2),
то по правилу умножения комплексных чисел
получим
z1 z2 = r1
r2 [(cos  1cos
1cos  2 - sin
2 - sin  1sin
1sin  2) + i(cos
2) + i(cos
 1sin
1sin  2 + sin
2 + sin  1cos
1cos
 2)] =
2)] =
= r1 r2 [cos( 1 +
1 +  2)
+ isin(
2)
+ isin( 1 +
1 +  2)].
2)].
Таким образом, при умножении
комплексных чисел их абсолютные величины
перемножаются, а аргументы складываются:
|z1z2| = |z1||z2|,
arg(z1z2) = arg z1 + arg z2 |
(2.8) |
(второе равенство является равенством двух
множеств). Отметим, что эту простую формулу для
аргумента произведения комплексных чисел нельзя
было бы написать, если бы мы с самого начала
ограничились однозначным выбором аргументов
комплексных чисел, например, с помощью
неравенств
- < arg z
< < arg z
<  , , |
(2.9) |
так как сумма arg z1 + arg z2
могла бы уже не удовлетворять этому неравенству,
хотя arg z1и arg z2 ему
удовлетворяли.
Применив последовательно формулы (2.8) к
произведению n комплексных чисел z1, z2, ... zn,
получим
|z1 z2 ... zn|
= |z1| |z2| ...| zn|,
arg (z1 z2 ... zn)
= arg z1 + arg z2 + ... + arg
zn.
Если z1 = z2 = ...= zn,
то из полученных равенств следует, что
|zn| = |z|n,
arg zn = n arg z + 2 k, k = 0, +1, +2,
... k, k = 0, +1, +2,
... |
(2.10) |
Следует обратить внимание на то, что
вторая формула (2.10) представляет собой равенство
множеств: если  -
какое-либо значение аргумента числа z и,
следовательно, n
-
какое-либо значение аргумента числа z и,
следовательно, n -
значение аргумента zn, то левая часть
равенства состоит из всех чисел вида
-
значение аргумента zn, то левая часть
равенства состоит из всех чисел вида
n + 2
+ 2 m, m = 0, +1, +2,
...,
m, m = 0, +1, +2,
...,
а правая - из всех чисел вида
n( + 2
+ 2 m) + 2
m) + 2 k = n
k = n + 2
+ 2 (nm + k),
(nm + k),
m = 0, +1, +2, ..., k = 0, +1,
+2, ...
Нетрудно убедиться, что эти два множества
состоят из одних и тех же чисел. Отсюда видно, что
arg zn 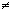 n arg z, так как здесь
правая часть состоит лишь из чисел вида
n arg z, так как здесь
правая часть состоит лишь из чисел вида
n( + 2
+ 2 m) = n
m) = n + 2
+ 2 nm,
nm,
т. е. таких чисел, которые получаются
прибавлением к числу n не всевозможных чисел вида 2
не всевозможных чисел вида 2 m, т. е. чисел, кратных 2
m, т. е. чисел, кратных 2 , а лишь чисел, кратных числу 2
, а лишь чисел, кратных числу 2 n.
n.
Отметим еще, что формула (2.10)
равносильна утверждению: если 
 arg z, то
arg z, то
n  arg zn. arg zn. |
(2.11) |
Поэтому если z = r (cos  + isin
+ isin  ), то
), то
zn = rn
(cos n + isin n + isin n ). ). |
(2.12) |
Отсюда для комплексного числа,
абсолютная величина которого равна 1
(следовательно, оно имеет вид
z = cos  + isin
+ isin
 ), получаем
), получаем
(cos  + isin
+ isin  ) = cos n
) = cos n + isin n
+ isin n .
.
Эта формула называется формулой Муавра. Если z = z1/z2,
z2 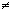 0, т. е. z1 = z2z,
то|z1| = |z2||z| и arg z1 = arg z2 + arg
z. Таким образом,
0, т. е. z1 = z2z,
то|z1| = |z2||z| и arg z1 = arg z2 + arg
z. Таким образом,
|z| = |z1|/|z2|,
arg z = arg z1 - arg
z2.
Иначе говоря, при делении комплексных чисел их
модули делятся, а аргументы вычитаются.
Извлечение корня. Если n -
натуральное число, z  C, то корнем
n-й степени
C, то корнем
n-й степени 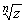 из
комплексного числа z называется такое
число w, что
из
комплексного числа z называется такое
число w, что
Например, числа i и -i
являются корнями степени 2 (квадратными
корнями) из числа z = -1, так как i2 = -1
и (-i)2 = -1. На этом примере уже
видно, что число 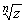 определено неоднозначно: для z = -1 может
быть
определено неоднозначно: для z = -1 может
быть
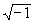 = i, а может быть
и
= i, а может быть
и 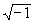 = -i. При этом,
в отличие от области действительных чисел, когда
можно было рассматривать положительные и
отрицательные значения корня, говорить о знаке
корня в комплексной области нельзя, так как
существенно комплексные числа не разбиваются на
положительные и отрицательные: у существенно
комплексного числа "нет знака". Поэтому при
употреблении записи
= -i. При этом,
в отличие от области действительных чисел, когда
можно было рассматривать положительные и
отрицательные значения корня, говорить о знаке
корня в комплексной области нельзя, так как
существенно комплексные числа не разбиваются на
положительные и отрицательные: у существенно
комплексного числа "нет знака". Поэтому при
употреблении записи 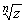 ,
,
z  C,
всегда надо отдавать себе отчет в том, что именно
в рассматриваемом случае обозначает собой
символ
C,
всегда надо отдавать себе отчет в том, что именно
в рассматриваемом случае обозначает собой
символ 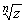 .
.
Если z = r (cos  + isin
+ isin
 ), w =
), w = 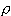 (cos
(cos 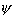 + isin
+ isin 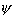 ) и wn =
z, то
) и wn =
z, то
Отсюда 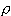 n = r,
а следовательно,
n = r,
а следовательно, 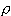 =
= 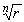 , где корень n-й
степени понимается в арифметическом смысле,
т. е.
, где корень n-й
степени понимается в арифметическом смысле,
т. е.
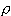 > 0, и
> 0, и
n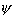 =
=  + 2
+ 2 k,
k = 0, +1, +2, ...,
k,
k = 0, +1, +2, ...,
или
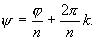
Для того чтобы получить все возможные
различные значения корней n-й степени, здесь
достаточно ограничиться лишь значениями k = 0, 1,
..., n - 1:
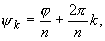
|
k = 0, 1, ..., n - 1, |
(2.14) |
так как при k = n получим 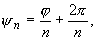 т. е. значение
аргумента
т. е. значение
аргумента 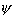 n
отличается от значения аргумента
n
отличается от значения аргумента
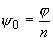 на 2
на 2 и при остальных значениях k будут
получаться значения угла
и при остальных значениях k будут
получаться значения угла 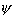 ,
отличающиеся от одного из значений
,
отличающиеся от одного из значений 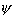 k, k = 0, 1, ..., n -
1, на кратное числа 2
k, k = 0, 1, ..., n -
1, на кратное числа 2 , а поэтому
соответствующее значение корня будет совпадать
с одним из чисел
, а поэтому
соответствующее значение корня будет совпадать
с одним из чисел
wk = 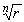 (cos (cos 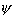 + isin + isin 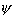 ),
k = 0, 1, ..., n - 1, ),
k = 0, 1, ..., n - 1, |
(2.15) |
Таким образом, корень n-й степени из числа z = r
(cos  + isin
+ isin  ) имеет n значений wk, для
которых справедливы формулы (2.14) и (2.15). Все
значения корня
) имеет n значений wk, для
которых справедливы формулы (2.14) и (2.15). Все
значения корня 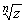 имеют
одинаковые модули
имеют
одинаковые модули 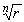 , а
аргумент
, а
аргумент 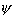 k корня wk
получается из аргумента
k корня wk
получается из аргумента 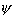 k-1
корня wk-1, k = 0, 1, ..., n
- 1, так же, как и аргумент
k-1
корня wk-1, k = 0, 1, ..., n
- 1, так же, как и аргумент 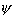 k
=
k
=  /n корня w0, -
из аргумента
/n корня w0, -
из аргумента 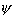 n-1
корня wn-1 прибавлением числа 2
n-1
корня wn-1 прибавлением числа 2 /n. Отсюда следует, что если
начало всех векторов wk, поместить в
начало координат, то их концы будут находиться в
вершинах правильного n-угольника. На
рис. 11 изображены корни
/n. Отсюда следует, что если
начало всех векторов wk, поместить в
начало координат, то их концы будут находиться в
вершинах правильного n-угольника. На
рис. 11 изображены корни 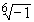 .
.
Сопряженные комплексные числа. Для
каждого комплексного числа z = x + iy
число x - iy называется ему сопряженным
и обозначается 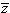 . Геометрический
вектор
. Геометрический
вектор 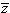 симметричен с вектором z
относительно действительной оси (рис. 12).
симметричен с вектором z
относительно действительной оси (рис. 12).
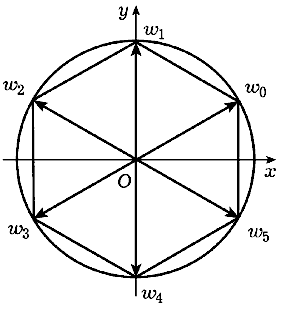
Рис 11. |
Рис.12 |
Перечислим основные свойства сопряженных
чисел.
1о. |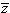 | = |z|, arg
| = |z|, arg 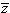 = arg z.
= arg z.
2о. z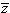 = |z|2.
= |z|2.
3о. 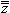 = z.
= z.
4о. 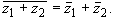
5о. 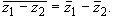
6о. 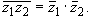
7о. 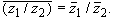
Докажем 1о: 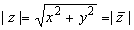 ; если z = r (cos
; если z = r (cos  + isin
+ isin
 ), то
), то 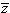 = r (cos
= r (cos  - isin
- isin  ) =
) =
= r ((cos (- ) + isin (-
) + isin (- )) , и потому arg
)) , и потому arg 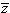 = arg
z..
= arg
z..
Докажем 2о: z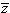 = (x + yi)(x - yi) = x2 + y2 = |z|2.
= (x + yi)(x - yi) = x2 + y2 = |z|2.
Так же просто доказывается  .
.
Свойства 4о и 5о вытекают из
симметричности сопряженных чисел относительно
действительной оси (рис.13 и рис.14), из которой
следует, что число 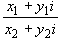 симметрично с z1 + z2, а число
симметрично с z1 + z2, а число 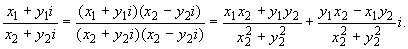 симметрично с z1 - z2.
симметрично с z1 - z2.
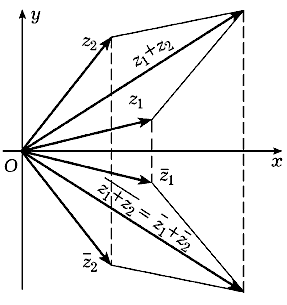
Рис. 13 |
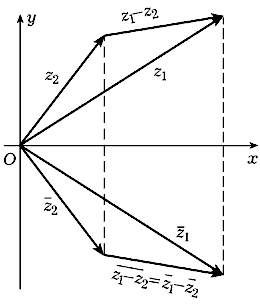
Рис. 14 |
Проверим теперь, что в формуле 6о
абсолютные величины и аргументы чисел, стоящих в
левой и правой частях равенства, равны:
|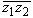 | | |
= |
|z1z2| |
= |
|z1||z2| |
= |
|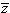 1|| 1||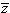 2| 2| |
= |
|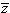 1 1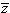 2| 2| |
|
1о |
|
(2.8) |
|
1о |
|
(2.8) |
|
arg (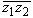 ) ) |
= |
arg (z1z2) |
= |
-(arg z1 + arg z2) |
= |
-arg z1 - arg z2 |
= |
arg 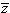 1 + arg 1 + arg 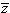 2 2 |
= |
arg (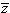 1 1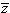 2). 2). |
|
1о |
|
(2.8) |
|
1о |
|
|
|
(2.8) |
|
Аналогично доказывается свойство 7о.
Используя сопряженные комплексные
числа, можно получить формулу для частного
комплексных чисел в алгебраической форме:
умножив числитель и знаменатель дроби 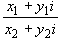 на число x2 - y2i,
сопряженное знаменателю, получим
на число x2 - y2i,
сопряженное знаменателю, получим
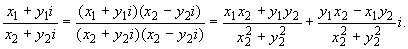
При построении теории комплексных
чисел мы исходили из того, что комплексным числом
называют объекты вида z = x + yi,
где x и y - действительные числа, а z -
некоторый новый элемент, называемый мнимой
единицей. Этому определению можно легко придать
строго логическую форму следующим образом.
Назовем комплексным числом
упорядоченную пару (x, y) действительных
чисел x и y. Операции сложения и умножения
для двух комплексных чисел (x, y) и (x', y')
определим по формулам
| (x, y) + (x', y') =
(x + x', y + y'), |
(2.16) |
| (x, y)(x', y') = (xx'
- yy', xy' + x'y). |
(2.17) |
Комплексные числа вида (x,0) будем обозначать
просто символом x:
а комплексное число (0,1) - символом i. Из
формулы (2.17) следует, что
i2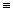 i i i
= (0,1)(0,1) i
= (0,1)(0,1) |
= |
(-1,0) = -1. |
|
(2.17) |
|
Для любого комплексного числа (x, y)
имеет место легко проверяемое тождество (x, y) = x + yi.
В самом деле,
(x, y) |
= |
(x,0) + (0, y) |
= |
(x,0) + (0,1)( y,0) |
= |
x + yi |
|
(2.16) |
|
(2.17) |
|
(2.18) |
|
Таким образом, мы пришли к
первоначальной записи комплексных чисел.
Расширенная числовая
прямая Оглавление Перестановки и сочетания







