3.3*. Многочлены

    Для изучения ряда свойств многочленов в действительной области, т. е. функций вида

P(x) = a_nxⁿ + ... + a₁x + a₀,

где  a₀, a₁, ..., a_n и x - действительные числа, оказывается целесообразным рассмотреть более общие функции: многочлены в комплексной области, т. е. функции вида

где a₀, a₁, ..., a_n и z - комплексные числа. Числа a₀, a₁, ..., a_n называются коэффициентами многочлена P(z). Если a_n0, то, как и выше, неотрицательное целое число n называется степенью многочлена P(z), который в этом случае обозначают иногда P_n(z).
   Два многочлена, P(z) и

равны тогда и только тогда, когда

  В самом деле, если выполняются эти равенства, то ясно, что многочлены (3.5) и (3.6) принимают одинаковые значения при всех z C.
    Наоборот, пусть при всех z справедливо равенство

Без ограничения общности можно предполагать, что m = n, так как при m  n можно добавить недостающие члены с нулевыми коэффициентами. Перенесем в равенстве (3.8) все члены в одну сторону и положим

В результате получим, что для всех z C выполняется равенство

В частности, это равенство имеет место для произвольно фиксированных n + 1 значений z₁, ..., z_n+1, отличных друг от друга: z_i z_j, i, j = 1, 2, ..., n + 1. Подставим z₁, ..., z_n+1 в равенство (3.10). Получим систему n + 1 линейных уравнений относительно n + 1 неизвестных ₀, ₁,  ... , _n

с определителем

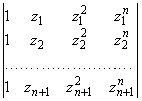
Из курса алгебры известно, что этот определитель, называемый определителем Вандермонда, равен произведению всевозможных разностей  z_j - z_i, j > i, и, следовательно, не равен нулю. Поэтому система (3.11) имеет единственное решение

₀ = ₁ = ... = _n+1 = 0.

Отсюда, в силу формулы (3.9), следует, что для коэффициентов многочленов (3.5) и (3.6) действительно имеют место равенства (3.7). 
    Сумма и произведение двух многочленов являются, очевидно, также многочленами. Чтобы перемножить два многочлена, достаточно перемножить их почленно и полученные результаты сложить:

Из этой формулы видно, что если ни один из перемножаемых многочленов не нулевой, то степень их произведения равна сумме их степеней. Если же по крайней мере один из них нулевой, то это свойство сохраняется в силу того, что степень нулевого многочлена равна - (см. п. 3.2).
    Если степень многочлена P(z) не меньше степени многочлена Q(z), то существуют единственные многочлены S(z) и R(z) такие, что

где степень многочлена R(z) меньше степени многочлена Q(z). При этом степень многочлена S(z) равна разности степеней многочленов P(z) и Q(z).
   Многочлен S(z) называется частным от деления многочлена P(z) на Q(z), а многочлен R(z) - остатком. Если R(z) = 0, то говорят, что P(z) делится на Q(z).
    Существование и единственность многочленов S(z) и R(z), удовлетворяющих соотношению (3.12) при заданных многочленах (3.5) и (3.6), b_m  0, можно доказать методом неопределенных коэффициентов.
Запишем многочлены S(z) и R(z) в виде

R(z) = c_m-1z^m-1 + ... + c₁z + c₀,
S(z) = c_nz^n-m + ... + c_m+1z + c_m.

    Подставим эти формулы в равенство (3.12):

произведем почленное умножение, сложим получившиеся результаты, сделаем приведение подобных членов и приравняем коэффициенты в левой и правой частях равенства при одинаковых степенях z. В результате получится система из n + 1 линейных уравнений относительно n + 1 неизвестных

c₀, c₁, ..., c_m-1, c_m, ..., c_n.

    Можно показать, что эта система имеет единственное решение, и даже найти его в явном виде методом математической индукции. В самом деле, для определения коэффициента c_n из равенства (3.13) получаем одно уравнение

a_n = c_nb_m,  b_m 0.

Далее возможны два случая: m < n и m = n. Если m < n, то для коэффициента c_n-1 из равенства (3.13) получается уравнение

a_n-1 = c_n-1b_m + c_nb_m-1,

в котором все коэффициенты, кроме c_n-1, известны. Если же m = n, то S(z) = c_n, a R(z) = c₀ + c₁z + ... + c_n-1z^n-1, и для коэффициента c_n-1 из (3.13) получаем уравнение

a_n-1 =  c_nb_n-1 + c_n-1.

Таким образом последовательно и однозначно находятся все коэффициенты (3.14). 

Понятие элементарной функции  Оглавление   Разложение многочленов на множители