3.5. Рациональные дроби

    Как в случае многочленов, мы рассмотрим рациональные дроби в комплексной области.
    Пусть P(z) и Q(z) - многочлены с, вообще говоря, комплексными коэффициентами и Q(z) не является нулевым многочленом. Рациональная дробь называется правильной, если степень многочлена P(z) меньше степени многочлена Q(z), и неправильной, если степень многочлена P(z) не меньше степени многочлена Q(z).
    Всякая рациональная дробь является либо правильной, либо неправильной. Если рациональная дробь неправильная, то, произведя деление числителя на знаменатель по правилу деления многочленов, т. е. представив числитель в виде

P(z) = S(z)Q(z) + R(z),

где S(z) и R(z) - некоторые многочлены, причем степень многочлена R(z) меньше степени многочлена Q(z), получим

= S(z) + .

Здесь в силу уже сказанного дробь является правильной.
    Займемся более подробно изучением правильных рациональных дробей.

    Лемма1. Если  - правильная рациональная дробь и число z₀ C является корнем кратности k > 1 ее знаменателя, т. е.

то существуют единственное число A C и многочлен P₁(z) такие, что

где дробь также является правильной.
    Если коэффициенты многочленов P(z) и Q(z) - действительные числа и корень z₀ многочлена Q(z) - также действительное число, то число A также является действительным числом, а многочлены
P(z) и Q(z) можно выбрать с действительными коэффициентами.
    Отметим, что здесь у многочленов P₁(z) и Q₁(z) единица является просто индексом, а не их степенью.
    Каково бы ни было число A C, прибавляя к дроби =  дробь, а затем вычитая ее, получим

=  = + =                                                                                                                    = +.

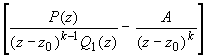(3.24)

    Степень многочлена P(z) по условию меньше степени многочлена Q(z) = (z - z₀)^kQ₁(z), а степень многочлена Q₁(z) меньше степени многочлена Q(z), поскольку Q(z) получается из Q₁(z) умножением на многочлен (z - z₀)^k, k > 1. Поэтому при любом выборе числа A C дробь

является правильной: степень ее числителя меньше степени знаменателя.
    Для того чтобы дробь (3.25) имела вид

необходимо и достаточно, чтобы ее можно было сократить на множитель (z - z₀), а это можно сделать в том и только том случае, когда числитель дроби (3.25) делится на (z - z₀), что согласно теореме Безу равносильно тому, что число z₀ является корнем многочлена, стоящего в числителе этой дроби, т. е. когда

P(z₀) - AQ₁(z₀) = 0.

Поскольку по условию Q₁(z₀) 0, то это равносильно тому, что

При таком и только таком выборе числа A дробь (3.25) сократится на (z - z₀), в результате в этом и только этом случае после сокращения дроби (3.25) получится дробь вида (3.26). Подставив эту дробь в равенство (3.24), получим разложение (3.23), в котором коэффициент A однозначно определен.
    Если корень z₀, а также коэффициенты многочленов P(z) и Q(z) являются действительными числами, то из равенства (3.22) следует, что и многочлен Q₁(z) имеет действительные коэффициенты. Поэтому в силу формулы (3.27) число A оказывается действительным, откуда следует, что и все коэффициенты многочленов, стоящих в числителе дроби (3.25), - также действительные числа. Следовательно, сокращая эту дробь на множитель (z - z₀), имеющий действительные коэффициенты, можно записать результат в виде рациональной дроби, у которой в числителе и знаменателе стоят многочлены с
действительными коэффициентами. 

   Теорема 1. Если  - правильная рациональная дробь и

где z₁, z₂, ..., z_N  - попарно различные корни многочлена Q(z), то существуют единственные комплексные числа , , ..., , j = 1, 2, ..., N, такие, что

    Применив последовательно k₁ раз лемму к дроби при z₀ = z₁, получим

=...                                                                   ... =... ,

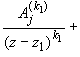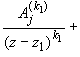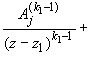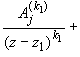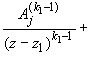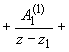(3.30)

где комплексные числа , ..., определяются последовательно единственным образом, P*(z) и Q*(z) - многочлены, причем  - правильная рациональная дробь и

Q*(z) = ... ,

Применив теперь аналогичным образом последовательно k₂ раз лемму 1 к дроби при z₀ = z₂, затем k₃ раз при z₀ = z₃ и т. д., k_N раз при z₀ = z_N, получим формулу (3.29). 
    Докажем еще одну лемму для правильных рациональных дробей, в числителях и знаменателях которых стоят многочлены с действительными коэффициентами.

    Лемма 2. Пусть P(x) и Q(x) - многочлены с действительными коэффициентами, причем  - правильная рациональная дробь.
    Если число z₀ = x₀ + y₀i, x₀ R,  y₀ R, y₀ 0, является корнем кратности m > 1 многочлена Q(x), т. е.

где

то существуют такие единственные действительные числа B, C и многочлен P₁(x) с действительными коэффициентами, что

где дробь

также является правильной.
    Для любых действительных B и C имеем

Рассуждениями, аналогичными проведенным при доказательстве леммы 1, легко убедиться, что дробь

является правильной и что коэффициенты многочленов, стоящих у нее в числителе и знаменателе, являются действительными. Для того чтобы дробь (3.35) имела вид

необходимо и достаточно, чтобы ее можно было сократить на множитель
x² + px + q = (x - z₀)(x - ₀), а это можно сделать тогда и только тогда, когда числитель дроби (3.35) делится на (x - z₀)(x - ₀), что согласно теореме Безу равносильно тому, что число z₀ является корнем многочлена, стоящего в числителе дроби (3.35), т. е. когда

P(z₀) - (Bz₀ + C)Q₁(z₀) = 0.

Поскольку Q₁(z₀) 0, то

Пусть = a + bi. Тогда равенство (3.37) можно записать следующим образом:

B(x₀ + y₀i) + C = a + bi.

Приравняв действительные и мнимые части комплексных чисел, стоящих в разных частях этого равенства, получим B = , C = a - . При таком выборе B и C они, во-первых, являются действительными числами, во-вторых, в этом и только этом случае число z₀, а следовательно, и сопряженное ему число ₀, являются корнями многочлена (3.37). При таком и только таком выборе чисел B и C дробь (3.35) сократится на
(x - z₀)(x - ₀). В результате в этом и только этом случае после сокращения дроби (3.35) получится дробь вида (3.36). Подставив эту дробь в равенство (3.34) вместо дроби (3.35), получим разложение (3.32), в котором действительные коэффициенты B и C однозначно определены. 

    Теорема 2. Пусть  - правильная рациональная дробь, P(x) и Q(x) - многочлены с действительными коэффициентами. Если

Q(x) = ,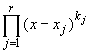

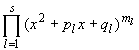где x_j - попарно различные действительные корни многочлена Q(x) кратности k_j,  j = 1, 2, ..., r, а
x² + p_lx + q_l = (x - z_l)(x - _l), где z_l, _l - попарно различные существенно комплексные корни многочлена Q(x) кратности m_l, l = 1, 2, ..., s, то существуют единственные действительные числа

, , ..., ,  j = 1, 2, ..., r,
, , ..., ,    , , ..., ,  j = 1, 2, ..., r,

такие, что

    Аналогично тому, как это было сделано в доказательстве теоремы 1, сначала последовательно применим лемму 1 k₁ раз при z₀ = x₁, затем k₂ раз при z₀ = x₂ и т. д., k_r раз при z₀ = x_r. В результате получим

где действительные числа , , ..., определяются последовательно единственным образом, коэффициенты многочленов P*(x), Q*(x) - действительные числа,  - правильная рациональная дробь, а

Q*(x) = .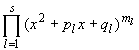

Применив к дроби последовательно лемму 2 m₁ раз при z₀ = z₁, затем m₂ раз при z₀ = z₂ и т. д., m_s раз при z₀ = z_s, получим

= .

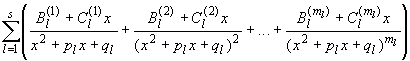    Подставив это выражение для в (3.39), получим доказываемую формулу (3.38).  
    Рациональные дроби вида

и , , m N,   n N,

называются элементарными, поэтому теоремы 1 и 2 называются теоремами о разложении правильных рациональных дробей на сумму элементарных (соответственно в комплексной и действительной областях).

  Разложение многочленов на множители Оглавление  Графики рациональных функций