 Рис. 15 |
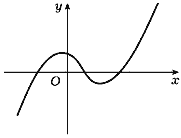 Рис. 16 |
График всякого многочлена степени n
с действительными коэффициентами пересекает
ось x в тех точках, абсциссы которых
являются его действительными корнями и тем самым
не более чем в n точках, так как он имеет не
более чем n корней.
Поведение многочлена при
неограниченном возрастании или неограниченном
убывании его аргумента зависит от четности
степени многочлена и знака при старшем члене.
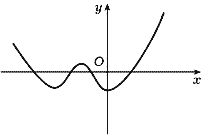
Если n - четное число и коэффициент при
старшем члене многочлена больше нуля, то как при
неограниченном возрастании аргумента, так и при
неограниченном его убывании значения многочлена
неограниченно возрастают (рис.15). Если n -
нечетное число, то при положительном
коэффициенте при старшем числе многочлена
значения многочлена неограниченно растут при
неограниченном возрастании аргумента и
неограниченно убывают при неограниченном его
убывании (рис. 16).
 Рис. 15 |
 Рис. 16 |
Если же коэффициент при старшем члене многочлена отрицателен, то при n четном многочлен неограниченно убывает как при неограниченном возрастании, так и при неограниченном убывании аргумента (рис. 17), а в случае n четного многочлен неограниченно убывает при неограниченном возрастании аргумента и неограниченно возрастает при неограниченном его убывании (рис. 18).
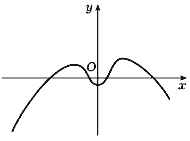 Рис. 17 |
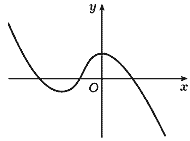 Рис. 18 |
Если P(x) - многочлен первого порядка:
P(x) = ax + b,
то его графиком является прямая линия.
Коэффициент a равен тангенсу угла
(см. п. 3.9), который эта прямая образует с
осью x, a b равно ординате точки
пересечения прямой с осью y (рис. 19).
В случае когда
рассматриваемый многочлен является квадратным
трехчленом ax2 + bx + c,
его график называется параболой.
Поскольку
у = ax2 + bx + c
|
(3.40) |
то график функции у = ax2 + bx + c
получается из параболы у = x2 ее
переносом на ![]() параллельно оси x, растяжением в |a| раз
вдоль оси x, симметрией относительно оси x
при a < 0 и переносом на
параллельно оси x, растяжением в |a| раз
вдоль оси x, симметрией относительно оси x
при a < 0 и переносом на ![]() параллельно оси y
(рис. 20). Из этого следует, что прямая x =
параллельно оси y
(рис. 20). Из этого следует, что прямая x = ![]() является осью симметрии
параболы (3.40), ибо ось y является осью
симметрии параболы у = x2. Точка
(
является осью симметрии
параболы (3.40), ибо ось y является осью
симметрии параболы у = x2. Точка
(![]() ,
, ![]() ) называется вершиной параболы (3.40).
) называется вершиной параболы (3.40).
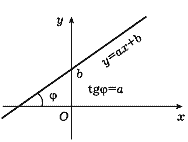 Рис. 19 |
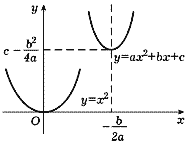 Рис. 20 |
Рациональная функция
y = |
(3.41) |
где P(x) и Q(x) - многочлены с
действительными коэффициентами, не имеющие
общих действительных корней (если бы нашелся
такой корень x0, то дробь (3.41) можно
было бы сократить на x - x0),
обращается в нуль в тех точках, в которых
обращается в нуль ее числитель P(x).
При этом если кратность нуля числителя четная, то
функция ![]() не
меняет знака в его окрестности, а если нечетная,
то меняет. В окрестности нулей знаменателя
значения рациональной функции неограниченно
возрастают по абсолютной величине при
приближении к указанным нулям.
не
меняет знака в его окрестности, а если нечетная,
то меняет. В окрестности нулей знаменателя
значения рациональной функции неограниченно
возрастают по абсолютной величине при
приближении к указанным нулям.
Если степень числителя рациональной
функции (3.41) больше степени ее знаменателя, то
при неограниченном возрастании по абсолютной
величине аргумента она также неограниченно
возрастает по абсолютной величине; если степень
знаменателя больше степени числителя, то она
неограниченно убывает по абсолютной величине;
если же степень числителя равна степени
знаменателя, то она неограниченно приближается к
отношению коэффициентов при старших членах
многочленов P(x) и Q(x).
Изучению поведения рациональных
функций помогает определение интервалов, на
которых рассматриваемая функция (3.41)
сохраняет постоянный знак. Все эти соображения
полезно использовать при построении графиков
рациональных функций.
В качестве примера построим график
функции
|
(3.42) |
Эта функция обращается в нуль в точках x = 0
и x = 1, причем в окрестности нуля она
меняет свой знак, а в окрестности единицы не
меняет. В окрестности точек x = -1 и x = +![]() она неограниченно
возрастает по абсолютной величине, причем в
точках x = +
она неограниченно
возрастает по абсолютной величине, причем в
точках x = +![]() меняет свой знак, а в точке x = -1 не
меняет.
меняет свой знак, а в точке x = -1 не
меняет.
При неограниченном возрастании по
абсолютной величине аргумента функция (3.42)
неограниченно приближается к нулю. Интервалы, на
которых она положительна или отрицательна,
изображены в следующей таблице:
| x | - |
- |
-1 | 0 | 1 | + |
|||||||
| y | -0 | - | + | + | 0 | - | 0 | - | + | +0 |
Проведенные рассуждения позволяют установить общий вид графика функции (3.42) (рис. 21). С помощью дальнейшего исследования этой функции ее график можно нарисовать более точно.
|