Рис. 22
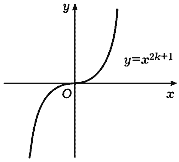
Рис. 23
Опишем поведение степенной функции y = xa
в случае, когда a - рациональное число (к
более подробному изучению степенной функции мы
вернемся в дальнейшем; см. п. 8.3).
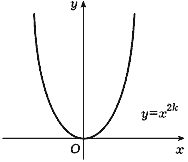
Рассмотрим сначала функцию y = xn,
где n - натуральное число. Эта функция
является частным случаем многочлена степени n
с n-кратным корнем x = 0. Согласно
сказанному в п. 3.6 при четном n ее график
имеет вид, изображенный на рис. 22, а при
нечетном n > 1 - на рис. 23.
Рис. 22 |
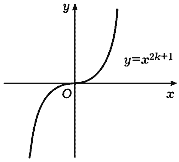Рис. 23 |
Функция y =
, где снова n -
натуральное число, является рациональной
функцией, неограниченно возрастающей при
приближении ее аргумента к точке x = 0.
Если n - четное число, то ее график имеет
вид, изображенный на рис. 24, а если n нечетное,
то - на рис. 25.
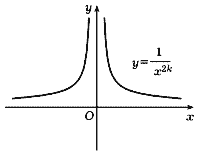 Рис. 24 |
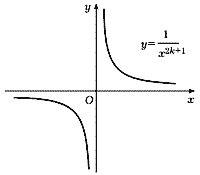 Рис. 25 |
Функция y = 
, где n - натуральное число, при n
нечетном определена на всей действительной оси,
а при n четном - только на полуоси x > 0
и принимает при x > 0 два значения. Если
ограничиться только неотрицательными
значениями корня, то и при четном n получится
однозначная функция.
Функция y = является
обратной к степенной функции y = xn.
Поэтому ее график симметричен относительно
биссектрис первого и третьего координатных
углов: при нечетном n > 1 он имеет вид,
изображенный на рис. 26, а при четном, если
ограничиться арифметическими значениями корня, -
на рис. 27.
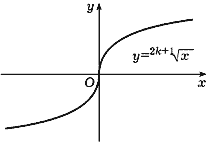 Рис. 26 |
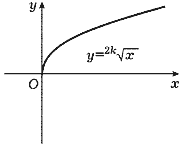 Рис. 27 |
График функции
y = xp/q, x > 0, |
(3.43) |
где p и q - целые числа, p/q > 1,
касается оси x (это естественнее всего
доказывается с помощью производной; см. п. 10.3). Если 0 < p/q < 1,
то q/p > 1 и, следовательно, в силу
сказанного график функции (3.43), или, что то же
самое, график функции y = xq/p,
касается оси y.
Если p/q > 0, то при
неограниченном возрастании x значение y
также неограниченно возрастает. Если p/q < 0,
то при неограниченном возрастании x
значение y неограниченно убывает, а при
неограниченном приближении x к нулю y
неограниченно возрастает.
При x < 0 функция y = xp/q
определена не для всех p и q. Если она
определена при x < 0, то является четной
или нечетной функцией, и потому ее график при x <
0 получается из ее графика при x > 0 с
помощью той или иной симметрии. В качестве
примера рассмотрим функцию y = x2/3.
Здесь p = 2 , q = 3,
следовательно, 0 < p/q < 1, и
функция определена при всех x.
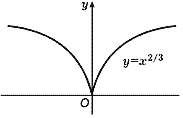 Рис. 28 |
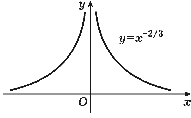 Рис. 29 |
В силу сказанного выше ее график (он
называется полукубической параболой) имеет
вид, изображенный на рис. 28.
В качестве второго примера рассмотрим
функцию y = x-2/3. Ее график
изображен на рис. 29.
Графики рациональных функций Оглавление Показательная и логарифмическая