3.9. Тригонометрические и обратные тригонометрические функции

    В прямоугольном треугольнике отношение катета, противолежащего данному углу треугольника, к гипотенузе называется синусом (sin ) этого угла, а отношение прилежащего катета к гипотенузе - косинусом (cos ) угла ; отношение противолежащего катета к прилежащему - тангенсом (tg ), а прилежащего к противолежащему - котангенсом (ctg ) угла (рис. 32). Из свойств подобных треугольников следует, что синус, косинус, тангенс и котангенс не зависят от размеров треугольника, а однозначно определяются углом ,

0 < < /2.

    Легко видеть, что они связаны соотношениями

    Для определения синуса, косинуса, тангенса и котангенса в случае произвольного угла , - < < +, рассмотрим на координатной плоскости переменных x, y окружности радиуса 1 с центром О в начале координат (рис. 33). Обозначим угол, который образует вектор , идущий из начала координат в точку А = (x, y), с положительным направлением оси x, иначе говоря, угол, на который надо повернуть единичный вектор оси x, Чтобы он совпал с вектором . При этом угол, который получается указанным вращением, считается положительным, если вращение производится против часовой стрелки, и отрицательным, если по часовой стрелке. Таким образом, угол , который образует вектор  с осью x, определен с точностью до целого, кратного полному обороту в ту или другую сторону. Следовательно, если  - величина угла в радианной мере, образованного вектором с осью x, то при любом целом n угол + 2n также будет углом, образованным этим вектором с осью x.
    Если 0 < < /2, то согласно данному выше определению

Если - произвольный угол, - < < +, и  - единичный вектор с координатами x, y, образующий угол  с осью x, то форму лы (3.45) принимаются за определение значений синуса и косинуса этого угла. Из них следует, что

Тангенс и котангенс произвольного угла определяются по формулам

Таким образом, они определены для всех тех , для которых знаменатели в правых частях равенств (3.47) не обращаются в нуль.
    Синус, косинус, тангенс и котангенс называются основными тригонометрическими функциями. Из их определения следует, что они являются периодическими функциями: при полном обороте (на 360^o в градусной мере или на 2 в радианной) в том или ином направлении радиус  займет прежнее положение, т. е. будет иметь те же самые координаты, а следовательно, синус, косинус, тангенс и котангенс примут прежние значения. Из формул (3.46) и (3.47) следует, что значения тангенса и котангенса будут повторяться и через пол-оборота. Таким образом, синус и косинус являются периодическими функциями с периодом 2 (мы будем пользоваться для измерения углов безразмерной радианной мерой, в которой угол задается действительным числом), а тангенс и котангенс - с периодом . Их графики изображены на рис. 34-37.

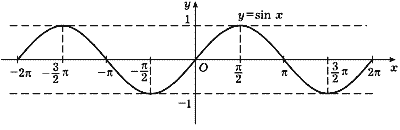Рис. 34
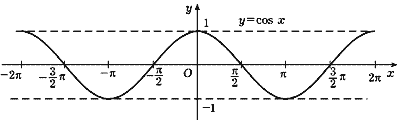Рис. 35
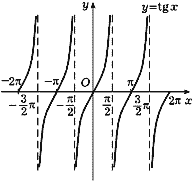Рис. 36	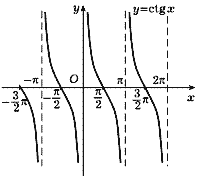Рис. 37

    Обратные функции для основных тригонометрических функций являются многозначными. Однако если функцию синус рассмотреть на отрезке [-/2, /2], косинус - на отрезке [0, ], тангенс - на интервале
[-/2, /2], а котангенс - на интервале [0, ], то обратные к ним функции будут уже однозначными и они обозначаются соответственно arcsin x, arccos x, arctg x и arcctg x. Функции arcsin x и arccos x определены на отрезке [-1, 1], а arctg x и arcctg x - на всей числовой прямой. Их графики изображены на рис. 38-41.

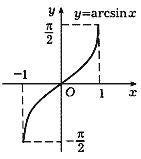Рис. 38	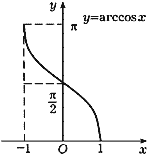Рис. 39
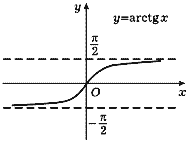Рис. 40	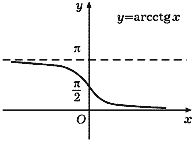Рис. 41

Показательная и логарифмическая  Оглавление  Параллельный перенос и растяжение графиков