4.1. Ограниченные и неограниченные множества

    Определение 1. Множество X 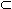 R называется ограниченным сверху, если существует такое число b  R, что для всех x  X имеет место неравенство x < b. Число b называется в этом случае числом, ограничивающим сверху множество X.
    Множество X называется ограниченным снизу, если существует такое число a  R, что для всех x  X выполняется неравенство x > a. Число a называется в этом случае числом, ограничивающим снизу множество X.
    Множество, ограниченное сверху и снизу, называется ограниченным.
    С помощью логических символов существования и всеобщности определение, например, ограниченного сверху множества можно записать следующим образом:

(здесь двоеточие означает "имеет место" или "выполняется условие").
    Множество, не являющееся ограниченным сверху, называется неограниченным сверху.
    Определение неограниченного сверху множества можно сформулировать и в позитивной форме, т. е. без отрицаний (без частицы "не"), следующим образом; множество X называется неограниченным сверху, если для любого числа b R найдется такой x  X, что x > b. Запишем это определение с помощью логических символов:

Сравнивая определения (4.1) и (4.2), видим, что при построении отрицания символ существования заменился на символ всеобщности, а символ всеобщности - на символ существования. Этим формальным правилом можно пользоваться при построении отрицаний в позитивной форме.
    Аналогично, множество, не являющееся ограниченным снизу, называется неограниченным снизу.
    Множество, не являющееся ограниченным, называется неограниченным.
    Множество натуральных чисел N является примером ограниченного снизу множества. Если a R и b R, то отрезок [a, b] представляет собой ограниченное множество. Множества рациональных чисел Q, иррациональных чисел I, вообще всех чисел R дают примеры неограниченных множеств.

Параллельный перенос и растяжение графиков  Оглавление   Верхняя и нижняя грани