5.4. Ограниченность сходящихся
последовательностей
Определение 5. Числовая
последовательность называется ограниченной
сверху (снизу), если множество ее значений
ограничено сверху (снизу).
Иначе говоря, числовая
последовательность {xn} ограничена
сверху (снизу), если существует такое число
c  R, что для всех номеров n
выполняется неравенство xn < c
(соответственно неравенство xn > c).
R, что для всех номеров n
выполняется неравенство xn < c
(соответственно неравенство xn > c).
Последовательность, ограниченная как
сверху, так и снизу, называется ограниченной.
Таким образом, числовая последовательность {xn}
ограничена, если существуют такие числа a  R
и b
R
и b  R, что для всех номеров n
выполняется условие a < xn < b.
Это условие, очевидно, равносильно тому, что
существует такое число c > 0, что для
всех номеров n имеет место неравенство
R, что для всех номеров n
выполняется условие a < xn < b.
Это условие, очевидно, равносильно тому, что
существует такое число c > 0, что для
всех номеров n имеет место неравенство
|xn| < c
Последовательность, не
являющаяся ограниченной сверху (снизу),
называется неограниченной сверху (снизу),
а последовательность, не являющаяся
ограниченной, называется неограниченой.
Примером неограниченных последовательностей
являются бесконечно большие последовательности
(см. п. 5.1, определение 3).
Следует заметить, однако, что не всякая
неограниченная последовательность является
бесконечно большой. Так, последовательность
xn = (-1)nn + n
неограниченная, но не бесконечно большая.
Теорема. Если числовая
последовательность имеет конечный предел, то
она ограничена.
 Пусть последовательность xn
Пусть последовательность xn  R,
n = 1, 2, ..., имеет конечный предел
R,
n = 1, 2, ..., имеет конечный предел 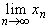 = a
= a  R.
Тогда согласно определению предела
последовательности (см.
п. 5.1, определение 1), взяв
R.
Тогда согласно определению предела
последовательности (см.
п. 5.1, определение 1), взяв  = 1, получим, что существует такой
номер n1, что для всех номеров n > n1
будет выполняться неравентсво
= 1, получим, что существует такой
номер n1, что для всех номеров n > n1
будет выполняться неравентсво
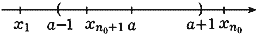
Рис. 51
|
(в определении предела последовательности
можно взять любое  >
0; мы взяли
>
0; мы взяли  = 1;
рис. 51). Обозначим через d наибольшее из
чисел 1, |x1 - a|, ...,
= 1;
рис. 51). Обозначим через d наибольшее из
чисел 1, |x1 - a|, ..., 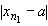 . Тогда, очевидно, в силу
условия (5.29) для всех
. Тогда, очевидно, в силу
условия (5.29) для всех
n  N будет иметь место
неравенство
N будет иметь место
неравенство
|xn - a| < d,
Это и означает, что последовательность {xn}
ограничена. 
Переход к пределу в
неравенствах Оглавление Бесконечно малые последовательности