5.5. Бесконечно малые последовательности
Над числовыми последовательностями
можно производить арифметические операции.
Определим их.
Определение 6. Пусть {xn}
и {yn} - числовые последовательности.
Тогда числовая последовательность {xn + yn}
называется их суммой {xn} + { yn},
{xn - yn} - их разностью
{xn} - { yn}, {xn yn} -
их произведением {xn}{ yn},
а если для всех номеров n выполняется
неравенство yn 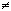 0, то последовательность
0, то последовательность 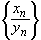 называется частным
называется частным 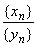 данных
последовательностей. Если
данных
последовательностей. Если  -
действительное число, то произведением
-
действительное число, то произведением  {xn} числовой
последовательности {xn} на число
{xn} числовой
последовательности {xn} на число  называется
последовательность {
называется
последовательность { xn}.
Таким образом, получается тот же результат, что и
от умножения стационарной последовательности {
xn}.
Таким образом, получается тот же результат, что и
от умножения стационарной последовательности { } на последовательность {xn}:
} на последовательность {xn}:
 {xn} = {
{xn} = { xn} = {
xn} = { }{xn}
}{xn}
Определение 1. Числовая
последовательность, предел которой равен нулю,
называется бесконечно малой.
Рассмотрим свойства бесконечно малых.
1o. Любая конечная линейная
комбинация бесконечно малых является бесконечно
малой.
 Пусть числовые
последовательности {
Пусть числовые
последовательности {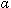 n}
и {
n}
и {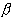 n}
бесконечно малые, т. е.
n}
бесконечно малые, т. е.
а  и
и 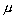 -
какие-либо действительные числа. Покажем, что
последовательность {
-
какие-либо действительные числа. Покажем, что
последовательность {
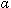 n +
n + 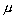
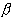 n}
также бесконечно малая. Зададим произвольно
n}
также бесконечно малая. Зададим произвольно  > 0 и возьмем
какое-либо число c такое, что
> 0 и возьмем
какое-либо число c такое, что
c > | |
+ | |
+ |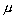 |. |. |
(5.31) |
Тогда, согласно определению
предела, из (5.30) следует, что существует
такой номер n0, что для всех номеров n > n0
выполняются неравенства
и, следовательно, неравенство
Это и означает, что
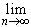 (
(
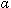 n +
n + 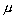
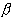 n)
= 0,
n)
= 0,
т. е. что последовательность {
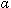 n +
n + 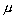
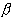 n}
бесконечно малая. Соответствующее
утверждение для любой конечной линейной
комбинации бесконечно малых следует из
доказанного методом математической индукции.
n}
бесконечно малая. Соответствующее
утверждение для любой конечной линейной
комбинации бесконечно малых следует из
доказанного методом математической индукции. 
2o. Произведение бесконечно
малой последовательности на ограниченную
последовательность является бесконечно малой.
 Пусть
Пусть
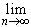 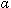 n = 0 n = 0
|
(5.33) |
и {xn} - ограниченная
последовательность, т. е. существует такое c > 0,
что для всех номеров n0 выполняется
неравенство
Зафиксируем произвольное  > 0, тогда согласно определению
предела из условия (5.33) следует, что существует
такой номер n0, что для всех номеров n > n0
имеет место неравенство
> 0, тогда согласно определению
предела из условия (5.33) следует, что существует
такой номер n0, что для всех номеров n > n0
имеет место неравенство
|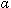 n|
< n|
<  /c, /c, |
(5.35) |
a следовательно, и неравенство
Это и означает, что 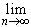
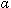 nxn = 0,
т. е. что последовательность {
nxn = 0,
т. е. что последовательность {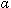 nxn} бесконечно малая.
nxn} бесконечно малая. 
Следствие. Произведение конечного
числа бесконечно малых последовательностей
является бесконечно малой.
 Если
Если
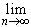
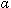 n
=
n
= 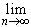
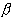 n = 0, то последовательность {
n = 0, то последовательность {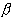 n}, имея
конечный предел, является ограниченной
последовательностью. Поэтому произведение {
n}, имея
конечный предел, является ограниченной
последовательностью. Поэтому произведение {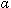 n
n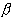 n} бесконечно малых
последовательностей {
n} бесконечно малых
последовательностей {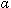 n}
и {
n}
и {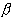 n}
можно рассматривать как произведение бесконечно
малой на ограниченную последовательность, и,
следовательно, согласно свойству 2o это
произведение является бесконечно малой
последовательностью. Соответствующее
утверждение для любого конечного числа
бесконечно малых последовательностей
получается из данного методом математической
индукции.
n}
можно рассматривать как произведение бесконечно
малой на ограниченную последовательность, и,
следовательно, согласно свойству 2o это
произведение является бесконечно малой
последовательностью. Соответствующее
утверждение для любого конечного числа
бесконечно малых последовательностей
получается из данного методом математической
индукции. 
Ограниченность сходящихся
последовательностей Оглавление
Свойства пределов, связанные с
арифметическими действиями над числовыми
последовательностями