5.6. Свойства пределов, связанные с арифметическими действиями над числовыми последовательностями

    Бесконечно малые последовательности играют в теории пределов особую роль, так как понятие конечного предела последовательности можно в определенном смысле свести к понятию бесконечно малой. Сформулируем это утверждение в виде леммы.

    Лемма 1. Числовая последовательность {x_n} имеет конечный предел, равный числу a, тогда и только тогда, когда последовательность

_n = x_n - a, n  = 1, 2, ...,

является бесконечно малой:

Пусть заданы числовая последовательность {x_n} и число a. Если _n = x_n - a, то условие = a согласно определению предела последовательности равносильно тому, что для любого > 0 существует такой номер
, что для всех номеров n > выполняется неравенство |x_n - a| < , т. е. неравенство _n < , а это равносильно тому, что _n = 0, т. е. тому, что последовательность {_n} бесконечно малая. 
    Утверждение леммы можно перефразировать следующим образом: число a является пределом последовательности {x_n} тогда и только тогда, когда x_n = a + _n, где {_n} - бесконечно малая последовательность.
    Рассмотрим свойства пределов числовых последовательностей.

     1^o. Если последовательность {x_n} сходится, то сходится и последовательность {|x_n|}, причем, если = a, то

Если = a, то для любого > 0 существует такой номер , что для всех номеров n > выполняется неравенство |x_n - a| < , а поскольку ||x_n| - |a|| < |x_n - a|, то выполняется и неравенство

||x_n| - |a|| <

а это и означает выполнение равенства (5.37). 

    2^o. Конечная линейная комбинация сходящихся последовательностей также является сходящейся последовательностью, и ее предел равен такой же линейной комбинации пределов данных последовательностей.
Пусть

Тогда в силу необходимости условий (5.36) для существования соответствующих конечных пределов члены последовательностей {x_n} и {y_n} можно представить в виде

где {_n} и {_n} бесконечно малые:

Пусть теперь и  - какие-либо числа. Тогда члены последовательности {x_n + y_n} представимы в виде

xn + yn	=	a + b + n + n,     n = 1, 2, ...,	(5.41)
	(5.39)

где последовательность { _n + _n} в силу бесконечной малости последовательностей {_n} и {_n} также бесконечная малая (см. свойство 1^o бесконечно малых последовательностей в п. 5.5):

Поэтому в силу достаточности условий (5.36) для существования соответствующего конечного предела из равенств (5.41) следует, что последовательность {x_n + y_n} имеет предел, равный a + b:

(x_n + y_n) = a + b,

или (см. (5.38))

Соответствующее утверждение для любой конечной линейной комбинации сходящихся последовательностей получается из доказанного методом математической индукции. 

    3^o. Если последовательности {x_n} и {y_n} сходятся, то их произведение {x_ny_n} также сходится:

т. е. предел произведения сходящихся последовательностей существует и равен произведению пределов данных последовательностей.
Пусть = a R, y_n = b R; тогда x_n = a + _n,  y_n = b + _n, n = 1, 2, ..., где _n = _n = 0. поэтому

причем последовательность {b_n + a_n} бесконечно малая как линейная комбинация бесконечно малых последовательностей {_n} и {_n}, а последовательность {_nn} бесконечно малая как произведение тех же последовательностей, поэтому бесконечно малой является и их сумма {b_n + a_n +   _nn}:

Из равенств (5.45) и (5.46) следует, что

x_n y_n = ab = x_ny_n. 

    Следствие. Если последовательность {x_n} сходящаяся и m - натуральное число, то

  = ()^m.

    Это непосредственно следует из свойства 3^o, так как возведение числа в целую положительную степень m сводится к повторному умножению на это число m раз.

    4^o. Если последовательности {x_n} и {y_n} сходятся, для всех номеров n имеет место неравенство y_n 0 и y_n 0, то последовательность сходится, причем

т. е. при сделанных предположениях предел частного сходящихся последовательностей существует и равен частному от пределов данных последовательностей.
Пусть = a R, y_n = b R,  b 0,  y_n  0, n = 1, 2, ...
Тогда x_n = a + _n,   y_n = b + _n, _n = _n = 0. Из условия y_n = b согласно свойству 1^o следует, что  |y_n| = |b|. Поскольку |b| > 0 (ибо b 0) и 0 < |b|/2 < |b|, то согласно следствию 1 из свойства 3^o пределов последовательностей (п. 5.3) существует такой номер n₀, что для всех n > n₀ выполняется неравенство |y_n| > |b|/2 и, следовательно, неравенство

(поскольку все  y_n  0, то на  y_n можно делить). Теперь имеем

Здесь последовательность

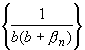
ограничена, ибо для всех n > n₀ выполняется неравенство

	<
	(5.47)

а последовательность {b_n - a_n} бесконечно малая как линейная комбинация бесконечно малых последовательностей {_n} и {_n}. Поэтому бесконечно малой является и последовательность

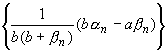
как произведение ограниченной последовательности на бесконечно малую. Следовательно, из равенства (5.48) вытекает, что

. 

Бесконечно малые последовательности   Оглавление    Монотонные последовательности