6.2. Определение непрерывности функции

    При рассмотрении предела функции  f(x), x X, в точке x₀ случай, когда x₀ X, представляет особый интерес - он приводит к понятию непрерывной функции.
    Если x₀ X и существует предел f(x), то он равен f(x₀):

В самом деле, поскольку x₀ X, то в качестве последовательности x_n X, n = 1, 2, ..., =  x₀, в этом случае можно взять стационарную последовательность x_n = x₀ , n = 1, 2, ... Для нее имеем

    Если существует предел f(x), то, согласно его определению, для любой последовательности x_n X, n = 1, 2, ..., для которой =  x₀, существует предел последовательности  f(x_n), n = 1, 2, ..., и все пределы таких последовательностей равны между собой. Поэтому из равенства (6.9) следует выполнение условия (6.8).

    Определение 5. Если

f(x) =  f(x₀),

то функция  f(x) называется непрерывной в точке x₀.  Согласно сказанному выше функция  f(x) непрерывна в точке x₀ тогда и только тогда, когда существует предел (по множеству X) f(x) и x₀ X. Например, функция   является непрерывной в точке x = 0 (как и во всякой другой точке x  1), ибо, как это было показано в п. 6.1,

Функция же

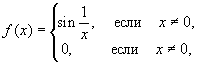
не является непрерывной в точке x = 0, так как предел sin 1/x не существует.

Первое определение предела функции  Оглавление  Второе определение предела функции