6.1. Первое определение предела функции

    В дальнейшем под термином "элемент", "точка" будет пониматься либо действительное число, либо одна из бесконечностей , + и - (бесконечно удаленные точки).
    Сформулируем сначала определение предела функции f: XR, X R, в терминах пределов последовательностей. Это определение часто называют определением предела функции по Гейне.

    Определение 1. Точка a называется пределом значений функции  f(x), x X (или, короче, пределом функции  f), в точке x₀ (или, что то же самое, при xx₀ (читается "при x, стремящемся к x₀), если для любой последовательности точек x_n X, n = 1, 2, ..., имеющей своим пределом точку x₀, т. е. такой, что

последовательность { f(x_n)} значений функции  f в точках x_n, n = 1, 2, ..., имеет своим пределом точку a, т. е.

    В этом случае пишут

а если x₀ - конечная точка: x₀ R, то также

f(x) = a.

    В символической записи с помощью логических символов это определение выглядит следующим образом

Двоеточием здесь, как и раньше в символических формулах (см. п. 1.1), отделяются описания рассматриваемых в условии элементов. В данном случае рассматриваются элементы x_n X, n = 1, 2, ..., такие, что x_n = x₀.
    Если в формуле (6.4) a является числом, то говорят, что функция  f имеет в точке x₀ конечный предел (равный a).
    Сформулированное определение предела при заданной функции f(x), x X, содержательно только тогда, когда для точки x₀ существуют последовательности точек x_n X, n = 1, 2, ..., имеющие своим пределом (конечным или бесконечным) точку x₀: x_n = x₀.

    Определение 2. Пусть X R. Точка x₀, для которой существует последовательность x_n X, n = 1, 2, ..., имеющая своим пределом точку x₀,

называется точкой прикосновения множества X.
    Если точка прикосновения является одной из бесконечностей , + или -, то она называется также бесконечно удаленной точкой прикосновения (множества X). Очевидно, что точка x₀ = является бесконечно удаленной точкой прикосновения множества X тогда и только тогда, когда множество X неограниченно, точка x₀ = + - тогда и только тогда, когда множество X неограниченно сверху, а x₀ = - - тогда и только тогда, когда X неограниченно снизу.
    Очевидно, что любая точка x₀, принадлежащая самому множеству X, является его точкой прикосновения, так как стационарная последовательность x_n = x₀ X, n = 1, 2, ..., удовлетворяет условию (6.5). Точками самого множества не исчерпываются, вообще говоря, все его точки прикосновения: могут существовать точки прикосновения, и не принадлежащие ему. Например, точки x = a и x = b являются точками прикосновения интервала (a, b) и не содержатся в нем.

    Замечание 1. Точка является точкой прикосновения данного множества тогда и только тогда, когда любая ее окрестность пересекается с этим множеством.
    В самом деле, если x₀ - точка прикосновения множества X, то существует последовательность
x_n x₀, x_n X,  n = 1, 2, ..., и, следовательно, в любой окрестности точки x₀ будут содержаться все члены этой последовательности, начиная с некоторого, и они являются точками множества X.
    Наоборот, если в любой окрестности точки x₀ имеются точки множества X, то выберем по точке множества X в каждой окрестности U(x₀,1/n) и обозначим эти точки через x_n, т. е.

x_n X U(x₀,1/n),  n = 1, 2, ...

Если x₀ R, т. е. x₀ является числом, то x_n U(x₀,1/n) означает, что |x_n - x₀| < 1/n. Отсюда при n   следует, что |x_n - x₀| = 0, т.е. x_n = x₀. Если же x₀ - бесконечно удаленная точка, например, x₀ = , то 
x_n U(,1/n) означает, что (см. п. 2.2) |x_n| = = n . Отсюда при n вытекает, что x_n = . Аналогично расматриваются случаи x₀ = + и x₀ = -. Таким образом, всегда из условия x_n U(x₀,1/n) следует, что x_n = x₀. Отметим, что нижняя и верхняя грани множества (конечные или бесконечные) являются его точками прикосновения. Поскольку понятие предела функции  f: XR в точке x₀ содержательно только тогда, когда эта точка является точкой прикосновения множества X, то в дальнейшем при рассмотрении предела функции  f в точке x₀ будем всегда предполагать (как правило, специально это не оговаривая), что точка x₀ является точкой прикосновения множества X.
    Примеры.
    1. Рассмотрим функцию

определенную на множестве X = R \{1}. Выясним, существует ли f(x).
Пусть x_n X,   n = 1, 2, ...,  и x_n = 0; тогда (п. 5.6)

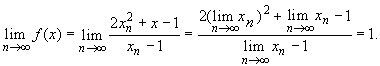
    Таким образом, существует предел f(x_n) = 1, а так как он не зависит от выбора последовательности
x_n0, x_n X,  n = 1, 2, ..., то существует и

f(x) = 1.

    2. Рассмотрим функцию

Она определена на множестве X = R \{0} (рис. 58). Выясним, существует ли предел f(x). Возьмем две последовательности:

и   n = 1, 2, ...

Очевидно

x_n = x'_n = 0,  x_n X,  x'_n X,
f(x_n) = sin n = 0,
f(x'_n) = sin (/2 + 2n) = 1,
n = 1, 2, ...

Поэтому

f(x_n) = 0, f(x'_n) = 1,

а это означает, что у рассматриваемой функции не существует предела в точке x₀ = 0.

    Определение 3. Если задана функция   f(x), x X, E X и x₀ - точка прикосновения множества E, то пределом функции f(x) по множеству E в точке x₀ называется предел ее сужения f_E (см. п. 1.2) в этой точке:

    Очевидно, что если существует f(x), то для любого множества E X, для которого точка x₀ является точкой прикосновения, существует f(x), причем эти пределы равны.
    Иногда при обозначении предела по множеству E вместо x E будут употребляться для краткости другие обозначения, смысл которых будет ясен из контекста. Например, при E = X \{x₀} будем писать
f(x), а при E = {x₀} будем писать f(x).
    3. Пусть

Эта функция называется функцией Дирихле. Имеем

f(x) = 1,     f(x) = 0,

а предел f(x) по всему множеству определения функции  f, т. е. по всему множеству действительных чисел, не существует. Часто пределы функций рассматриваются по пересечениям областей определения этих функций с так называемыми проколотыми окрестностями.

    Определение 4. Проколотой -окрестностью (x₀,) точки x₀ называется множество, получающееся удалением точки x₀ из ее -окрестности:

    Проколотую окрестность будем также обозначать и через U(x₀).
    Пример 4. Пусть

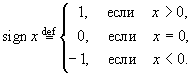
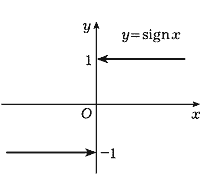Рис. 59

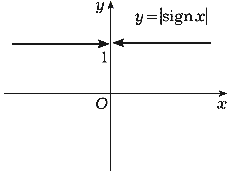Рис. 60

Тогда (рис. 59 и рис. 60) предел |sign x| функции |sign x| по всей ее области задания, т. е. по всей числовой прямой (или, что равносильно, по любой окрестности U(0) точки x₀ = 0), не существует, а предел этой функции по проколотой окрестности (0) точки x₀ = 0 существует и равен 1: .
    Действительно, для любой последовательности x_n (0), n = 1, 2, ..., x_n = 0, имеем  f(x_n) = 1, а поэтому f(x_n) = 1. Это означает, что  = 1, т. е. что предел по проколотой окрестности существует и равен 1. Если же x'_n = 1/n, x"_n = 0, n = 1, 2, ..., то x'_n = x"_n = 0, и  f(x'_n) = 1,  f(x"_n) = 0. Поэтому f(x'_n) = 1, а f(x"_n) = 0. Это означает, что предел по всей окрестности U(0) не существует.

    Замечание 2. Пусть заданы последовательность {x_n} и функция : NN. Введем обозначение (k) = n_k и рассмотрим последовательность {}. Иначе говоря, из значений последовательности {x_n} образуем новую последовательность {}, в которой порядок членов может не совпадать с их порядком в исходной последовательности. Таким образом, последовательность {} не является, вообще говоря, подпоследовательностью последовательности {x_n}. В этих обозначениях справедливо следующее утверждение.

    Лемма 1. Если существует конечный или бесконечный предел
x_n = a, и n_k = то = a.
Действительно, из условия x_n = a следует, что для любого  > 0 существует такой номер n₀, что для всех номеров n > n₀ выполняется включение x_n U(a,) , а из условия n_k = , - что для n₀ существует такой номер k₀, что для всех k > k₀ выполняется неравенство n_k > n₀ и, следовательно, включение
U(a,). Это и означает, что = a. 
    Из леммы 1 следует, что понятие предела последовательности является частным случаем понятия предела функции.
Действительно, пусть предел последовательности {x_n} равен a: x_n = a. Рассмотрим функцию f(n) = x_n, n N. В силу леммы 1 для любой последовательности вида {}, n_k N, n_k = , имеем = a, т. е.  f(n_k) = a. Согласно определению 1 это и означает, что f(n) = a. 

Предел последовательности комплексных чисел  Оглавление  Определение непрерывности функции