6.11. Пределы монотонных функций
Определение 13. Функцию f(x),
x 
X,
называют возрастающей (соответственно убывающей)
на множестве X и пишут f
(соответственно f
), если
для любых x1 X и x2 X таких, что x1 < x2,
выполняется неравенство f(x1) <
f(x2) (соответственно f(x1) >
f(x2)).
Возрастающие и убывающие функции
называются монотонными.
Если из неравенства x1 < x2,
x1 X,
x2 X,
следует, что f(x1) < f(x2)
(соответственно, что f(x1) >
f(x2)), то функцию f называют строго
возрастающей (строго убывающей) и пишут f (соответственно f). Строго возрастающие
и строго убывающие функции называются строго
монотонными. Если функция f (строго)
возрастает на множестве X, то функция -f
(строго) убывает на этом множестве.
Верхней гранью sup f
функции f(x), x X (или, в другой записи, 
f(x)),
называется верхняя грань значений этой функции
на множестве ее задания X:
sup f 
{ f(x)},
а нижней гранью inf f (или 
{ f(x)}
) - нижняя грань ее значений:
inf f { f(x)}.
Если функция f принимает в точке x0
наибольшее значение на множестве X, то,
очевидно, f(x0) = sup f,
а если она принимает в точке x0
наименьшее значение, то f(x0) = inf f.
Теорема 4. Пусть функция
f(x), x
X, возрастает на множестве X, 
= inf X, 
= sup X, 
X, X.
Тогда у функции f существуют конечные
или определенного знака бесконечные пределы
справа в точке
x = :
 f(x)
= f(x),
|
(6.28) |
и слева в точке x = :
f(x)
= f(x), |
(6.29) |
Таким образом, если функция f
ограничена снизу (т. е. ограничено снизу
множество ее значений), то предел (6.28) будет
конечным, а если f не ограничена снизу, то этот
предел будет бесконечным, равным -
. Аналогично, предел (6.29) будет
или клнечным или бесконечным, равным +, когда функция f
ограничена сверху или соответственно не
ограничена сверху.
Пусть функция f возрастает на
множестве X и
b = f(x) < +. |
(6.30) |
Зададим произвольно окрестность U(b)
точки b, и пусть 
-
левый конец этой окрестности (рис. 67); тогда
< b и
существует такое 
X, что
f() > . |
(6.31) |
Из того, что =
sup X, следует, что < , но , а по условиям теоремы X, поэтому < .
Обозначим через U() окрестность точки , левым концом которой является
точка (см. рис. 67).
Тогда если
то < x < и, следовательно, в
силу возрастания функции f будет
выполняться неравенство
Поэтому
|
< |
f(x) < f(x) |
= |
b. |
(6.34) |
|
(6.31)
(6.32) |
|
(6.30) |
|
|
Вспоминая, что точка является левым концом окрестности
U(b), получим из (6.34)
f(x) U(b) |
(6.35) |
Аналогично рассматривается
случай предела функции f при x
. 
Следствие. Если функция f
возрастает на множестве X, x0 X, множества X_(x0),
X+(x0) не пусты и точка x0
является их точкой прикосновения, то функция f
имеет в этой точке конечные пределы f(x0 - 0)
и f(x0 + 0), причем
f(x0 - 0) <
f(x0 + 0). |
(6.36) |
Напомним, что запись x0 x0 + 0 (соответственно
запись x0 x0
- 0) означает, что рассматривается предел справа
(слева) по множеству, не содержащему точки x0.
Если функция f
возрастает на множестве X, то для любых x' X_(x0) и
x" X+(x0)
выполняется неравенство
Иначе говоря, возрастающая функция f
ограничена числом f(x") сверху на
множестве X_(x0) и числом f(x')
снизу на множестве X+(x0).
Поэтому согласно теореме 4 существуют
конечные пределы f(x0 - 0) и
f(x0 + 0). Перейдя к верхней
грани в левой части неравенства (6.37), получим
f(x) <
f(x"),
а перейдя здесь в правой части к нижней грани,
будем иметь
f(x)
<  f(x") |
(6.38) |
Согласно теореме 4
f(x0 - 0) = f(x),
f(x0 + 0)
= f(x"),
x X.
Поэтому неравенство (6.38) совпадает с
неравенством (6.36).
Замечание1. Теорема, аналогичная
теореме 4, справедлива и для убывающих функций.
Замечание 2. Если функция f
возрастает на множестве X, = sup X и X, то предел 
функции f по всякому X (т. е. включая ) может существовать
(рис. 68), тогда функция f будет непрерывна в
точке x = (см.
п. 6.2), а может и не существовать (рис. 69),
тогда точка будет
точкой разрыва функции f. Подчеркнем,
однако, что согласно теореме 4 предел 
всегда существует.
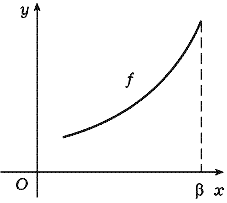Рис. 68 |
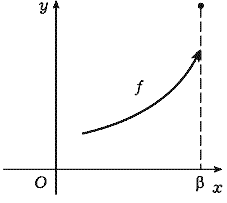Рис. 69 |
Классификация точек
разрыва Оглавление Критерий Коши существования предела
U(