10.3. Геометрический смысл производной и дифференциала

    Пусть функция f определена в некоторой окрестности U(x₀) точки x₀, непрерывна в этой точке, y₀ = f(x₀) и M₀ = (x₀,y₀) (рис. 74). Зафиксируем произвольно приращение аргумента x, лишь бы x₀ + x U(x₀), и пусть

y =   f(x₀ + x)  -  f(x₀),   M = (x₀ + x, y₀ + y).

    Уравнение прямой, проходящей через точки M₀ и M, - она называется секущей (графика функции f) - имеет вид

    Подчеркнем, что здесь x фиксировано, а x и y - текущие координаты точек прямой. Если задано семейство прямых уравнениями

где t - параметр (в случае уравнения (10.15) параметром служит x), и существуют конечные пределы

a(t) = a₀,   b(t) = b₀,   c(t) = c₀,

то говорят, что прямые стремятся при tt₀ к предельному положению - к прямой, уравнением которой является уравнение

a₀x + b₀y + c₀ = 0.

Для того чтобы секущая (10.15) при x0 стремилась к предельному положению, отличному от вертикальной прямой, необходимо и достаточно, чтобы существовал конечный предел (y/x), т. е. чтобы существовала конечная производная. При этом уравнение предельного положения секущей, которое называется касательной к графику функции f в точке M₀, имеет вид

Отметим, что из непрерывности функции f в точке x₀ следует, что y = 0, а поскольку
|M₀M| = (x² + y²)^1/2 , то и |M₀M| = 0, т. е. точка M "стремится к точке M₀" по графику функции f.
    Вспомнив геометрический смысл коэффициента при x - x₀ в уравнении (10.17), получим

f'(x₀) = tg ,

где  - угол наклона касательной к оси OX (см. рис. 74). Обозначим ординату касательной через  y_кас; тогда, положив x - x₀ = x, запишем уравнение касательной (10.17) в виде

y_кас - y₀ =  f'(x₀)x.

В правой части этого равенства стоит дифференциал dy функции f в точке x₀. Таким образом,

- дифференциал функции равен приращению ординаты касательной. Рассмотрим случай бесконечной производной

Из уравнения секущей (10.15) имеем

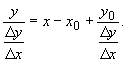
Переходя здесь к пределу при x0, в случае выполнения условия (10.19) получим уравнение предельного положения секущей, т. е. касательной к графику функции f в точке x₀, в виде

x = x₀,

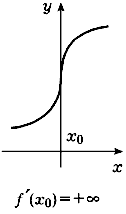
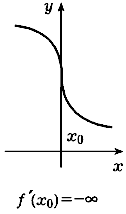
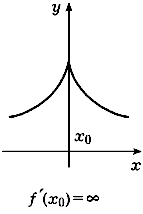
т. е. касательная в этом случае является вертикальной прямой, проходящей через точку x₀ оси абсцисс (рис. 75).

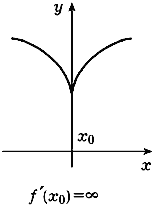Рис. 75

Дифференциал функции   Оглавление   Физический смысл производной