10.8. Гиперболические функции и их производные

    Нередко в математическом анализе встречаются функции (e^x - e^-x)/2 и (e^x + e^-x)/2. Они имеют специальные названия: первая из них называется гиперболический синус и обозначается sh x, а вторая - гиперболический косинус ch x. Таким образом,

	(10.35)
	(10.36)

    Эти функции обладают некоторыми свойствами, похожими на свойства обычных (круговых) синусов и косинусов, например,

ch2x - sh2x = (e2x + 2 - e-2x - e2x + 2 - e-2x)/4 = 1,	(10.37)
2ch xsh x = 2(ex - e-x)/2(ex + e-x)/2 = (e2x - e-2x)/2 = sh 2x.	(10.38)

    Слово "гиперболический" в названии функций (10.35) и (10.36) объясняется тем, что уравнения

x = ach t,   y = ash t,   a > 0, - < t < +.

являются, в силу формулы (10.37), параметрическими уравнениями правой ветви гиперболы x² - y² = a², подобно тому, как уравнения

x = acos t,   y = asin t,   0 < t < 2,

являются параметрическими уравнениями окружности x² + y² = a². Вычислим производные гиперболических синуса, косинуса:

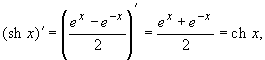	(10.39)
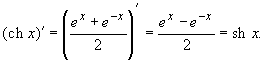	(10.40)

Производная и дифференциал сложной функции Оглавление Производные комплекснозначных функций действительного аргумента