, то она называется второй
производной функции f в точке x0
и обозначается f"(x0) или f(2)(x0).
Таким образом, опуская обозначения аргумента,
имеем Пусть функция y = f(x)
имеет производную y' = f'(x) во всех
точках некоторой окрестности точки x0.
Если функция f'(x) в свою очередь имеет в
точке x0 производную , то она называется второй
производной функции f в точке x0
и обозначается f"(x0) или f(2)(x0).
Таким образом, опуская обозначения аргумента,
имеем
y(2) 
y" 
(y')'.
Аналогично определяются и производные y(n) более высоких порядков n:
y(n+1) = [y(n)]', n = 0, 1, 2, ..., |
(11.1) |
где для удобства считается, что y(0) = y.
Примеры.
1. Если y = ax, a > 0,
то y' = ax ln a, y" = ax ln2 a,
вообще, y(n) = ax lnn a,
n = 0, 1, 2, ... В частности, если y = ex,
то
(ex)(n) = ex. |
(11.2) |
2. Если y = sin x, y' = cos x,
y(2) = -sin x, y(3) = -cos x,
y(4) = sin x. Заметив, что cos x
= sin (x + 
/2), получим
y' = sin(x + /2), y(2) = cos (x
+ /2) = sin(x + 2/2).
Вообще,
sin(x)(n) = sin(x
+ n |
(11.3) |
Аналогично,
cos(x)(n) = cos(x
+ n |
(11.4) |
Теорема 1. Если функции y1 = f1(x)
и y2 = f2(x) имеют
в точке x0 производные порядка n
N,
то любая их линейная комбинация 
1y1 + 2y2 , 1 R, 2 R, и
их произведение y1y2
имеют в точке x0 производные
порядка n, причем
| (1y1 +
2y2)(n)
= 1y1(n) +
2y2(n), |
(11.5) |
 |
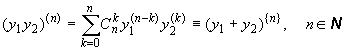(11.6) |
Все производные в формулах (11.5) и (11.6)
берутся в точке x0, 
- биномиальные коэффициенты.
Символическая запись (y1 + y2){n}
означает, что это выражение (см. среднюю часть
формулы (11.6)) по своей структуре напоминает
формулу бинома Ньютона
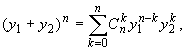
только вместо степеней y1 и y2
берутся производные соответствующих порядков
функций y1 и y2. Формула (11.6)
называется формулой Лейбница.
Докажем формулы (11.5) и (11.6)
методом математической индукции. В п. 10.5 формула
(11.5) была доказана для n = 1:
( |
(11.7) |
Пусть справедлива формула (11.5); покажем, что тогда будет справедлива и аналогичная формула для производной порядка n + 1:
Формула (11.5) доказана; докажем формулу (11.6).
Пусть справедлива формула (11.6) для
производной порядка n от произведения
функций. Докажем, что тогда будет справедлива и
аналогичная формула для производной порядка n + 1:
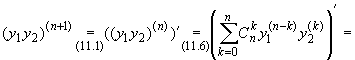
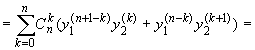
Вспомнив, что (см. п. 2.4)
получим
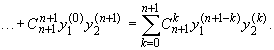
Производные комплекснозначных функций действительного аргумента Оглавление Производные высших порядков сложных функций, обратных функций и функций, заданных параметрически