13.1. Неопределенности вида 0/0

    Теорема1. Если функции f и g определены в окрестности точки x₀,

существуют конечные производные g'(x₀)0 и f'(x₀), то существует предел

Действительно,

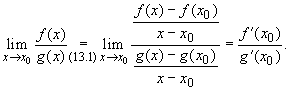
    Геометрический смысл равенства (13.2) состоит в том, что предел отношения ординат графиков функций f и g равен пределу отношения ординат из y = f'(x₀)(x - x₀) и y = п'(x₀)(x - x₀) касательных которое постоянно и равно  (рис. 81).
    Теорема 2. Если:
1) функции f и g дифференцируемы на интервале (a,b);
2) g'(x)0 для всех x (a,b);
3) f(x) = g(x) = 0.
4) существует конечный или бесконечный предел ; то существует и предел , причем

Доопределим функции f и g в точке x = a по непрерывности, т. е. положим

Тогда для любого x (a,b) продолженные функции на отрезке [a,x] будут удовлетворять условиям теоремы Коши о среднем значении, и потому будет существовать такая точка = (x), a <  < x, что

Поскольку (x) = a и предел существует, то

и, следовательно, существует

Неопределенности вида 0/0  Оглавление  Неопределенности вида бесконечность/бесконечность