13.2. Неопределенности вида бесконечность/бесконечность

    Теорема 3. Если:
    1) функции f и g дифференцируемы на интервале (a,b);
    2) g'(x)0 для всех x (a,b);

    4) существует конечный или бесконечный предел ; то существует предел и

Пусть существует конечный или бесконечный предел

Покажем, что при выполнении остальных условий теоремы

Если a < x < x₀ < b, то на отрезке [x,x₀]  функции f и g удовлетворяют условиям теоремы Коши (см. теорему 4 в п. 12.2), а поэтому существует такая точка = (x₀,x), что

Далее, в силу (13.7) существует такая точка x₁ = x₁(x₀,),   a < x₁ < x₀, что при всех x (a,x₁) выполняются неравенства

f(x)0,
g(x)0,
f(x)f(x₀),

и, следовательно, можно производить деление на f(x), g(x) и 1 - f(x₀)/f(x) (а также и на 1 - g(x₀)/g(x), поскольку в силу условий теоремы g(x)g(x₀); см. (12.16) в доказательстве теоремы 4 из п. 12.2). Для этих значений x из (13.11) вытекает равенство

= ,

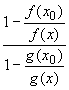откуда

В правой части равенства первый сомножитель стремится к числу k при x₀a (ибо a <  < x₀, и поэтому ), а второй в силу условия (13.7) стремится к 1 при xa и фиксированном x₀:

    Непосредственно перейти к пределу в равенстве (13.12) нельзя, так как указанные выше предельные переходы в сомножителях в правой части равенства происходят при разных условиях: при x₀a и при фиксированном x₀, но xa. Однако если задать произвольно окрестность U(k) предела k отношения производных (13.9), то можно сначала зафиксировать точку x₀ столь близко к точке a, что отношение   попадет в эту окрестность, ибо a <  < x₀. Согласно же условию (13.13) для всех точек x, достаточно близких к a, отношение  (см. (13.12)) также будет принадлежать указанной окрестности U(k), а это означает справедливость утверждения (13.10).
    Проведенное рассуждение нетрудно записать с помощью неравенств.
    Пусть сначала предел (13.9) конечный. Положим

Тогда из (13.9) будем иметь (x) = 0, и, следовательно, для любого произвольно фиксированного > 0 существует такое x₀, что для всех x (x,x₀) выполняется неравенство

Если положить еще

то в силу условия (13.7)

Теперь имеем

x <  < x₀; при этом в силу (13.17) существует такое > 0, a < a +   < x₀, что при x (a,a+) выполняется неравенство

    В результате получаем, что для всех x (a,a+) выполняется неравенство

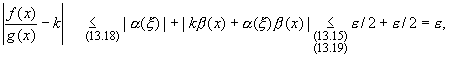
а это и означает выполнение равенства (13.10).
    Если теперь

то = 0, откуда по уже доказанному = 0, и потому

    Из (13.20) и (13.21) следует, что (13.8) справедливо и в этом случае.
    Аналогично рассматривается и случай бесконечного предела со знаком. Более того, можно показать, что в условиях теоремы бесконечный предел (13.9) всегда является бесконечностью со знаком. 
    В теоремах 2 и 3 был рассмотрен случай, когда аргумент стремился к числу a справа. К этому случаю сводятся случаи, когда аргумент x стремится к числу a слева или произвольным образом, а также случаи, когда a является одной из бесконечностей , + или -. Во всех этих случаях при соответствующих предположениях имеет место формула

    Рассмотрим, например, случай стремления аргумента к + для функций f и g, заданных на полуинтервале вида [c,+], где c - некоторое число. Этот случай сводится к случаю, рассмотренному в теореме 3 с помощью замены переменного x = 1/t. В самом деле,

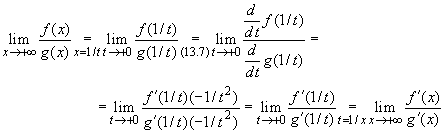
(здесь штрихом обозначены производные функций f и g по первоначальному аргументу x).
    Правило вычисления предела отношений функций по формуле (13.22) называется правилом Лопиталя.

    Примеры.
    1. Если  > 0, то

т. е. любая положительная степень x возрастает быстрее ln x при x+. Действительно, применив правило Лопиталя, получим

    2. Если  > 0, и a > 0, то

т. е. при x+ любая степень ,  > 0, растет медленнее показательной функции с основанием, большим единицы. В самом деле, сделав указанные ниже преобразования и применив правило Лопиталя, получим

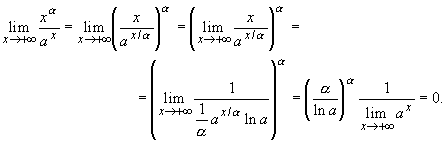
3. Найдем [x²sin (1/x) / sin x]. Здесь отношение производных числителя и знаменателя

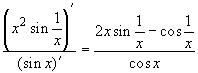
не стремится ни к какому пределу при x0 и, следовательно, правило Лопиталя неприменимо. В этом случае предел находится непосредственно:

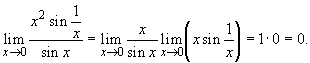
    Из этого примера следует, что предел

может существовать в случае, когда предел

не существует, и, тем самым, здесь для нахождения предела (13.25) правило Лопиталя (13.22) неприменимо.    
    4. Предел неопределенностей типа 0⁰, ⁰ или можно найти, предварительно прологарифмировав функции, предел которых ищется. Например, чтобы найти предел x^x, найдем сначала предел

Отсюда в силу непрерывности показательной функции будем иметь

В частности, при x = 1/n  получим

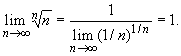
    5. Пределы неопределенностей типов 0 и - целесообразно привести к виду или . Например,

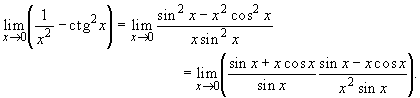
Предел первого сомножителя в правой части находится непосредственно:

а предел второго -- с помощью правила Лопиталя:

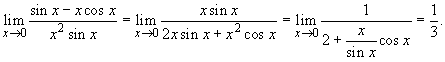
Таким образом, .

Неопределенности вида 0/0  Оглавление  Вывод формулы Тейлора