15.4. Асимптоты

    Определение 6. Если функция f задана для всех x > a (соответственно для всех x < a) и существует такая прямая

что

(соответственно при x-), то эта прямая называется асимптотой функции f при x+ (соответственно при x-).
    Конечно, далеко не всякая функция имеет асимптоты. Существование асимптоты функции означает, что при x+ (или при x-) функция ведет себя "почти как линейная функция", т. е. отличается от линейной функции на бесконечно малую.
    Укажем методы отыскания асимптот (15.20). Будем рассматривать лишь случай x+; для x- вывод уравнения асимптоты производится аналогичным способом. Пусть функция f при x+ имеет асимптоту (15.20). Тогда поскольку (1/x) = 0, то из условия (15.21) следует, что тем более

[(f(x) - kx - l)/x] = 0,    т. е.  [(f(x)/x - k - l/x] = 0

откуда

Если значение k найдено, то значение l находится из условия (15.21):

    Очевидно, справедливо и обратное утверждение: если существуют такие числа k и l, что выполняется условие (15.23), то прямая y = kx + l является асимптотой функции f при x+, так как из (15.23) сразу следует условие (15.21).

    Пример. Найдем асимптоту функции

Согласно формулам (15.22) и (15.23) имеем ,

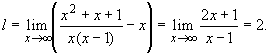
Отсюда следует, что асимптотой функции (15.24) является прямая y = x + 2.
    Уравнениями вида (15.20) описываются все прямые, которые не параллельны оси Oy, т. е. не вертикальны. Поэтому асимптоты вида (15.20) называют также и наклонными асимптотами. Сформулируем теперь определение вертикальных асимптот.
    Определение 7. Если для функции f выполнено хотя бы одно из условий

то прямая x = x₀ называется вертикальной асимптотой функции f.
    Для того чтобы имело смысл рассматривать первый (второй) предел (15.25), здесь предполагается, что функция f задана на пересечении некоторой окрестности точки  x₀ с лучом  x < x₀ (с лучом  x > x₀). Чтобы найти вертикальные асимптоты функции f, надо найти такие значения x₀, для которых выполняются одно или оба условия (15.25). Например, для функции (15.24) вертикальной асимптотой является прямая x = 1, ибо

Выпуклость и точки  Оглавление  Построение графиков функций