15.3. Выпуклость и точки перегиба

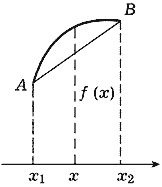
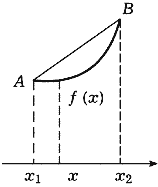
    Пусть функция f задана на интервале (a,b) и a < x₁ < x₂ < b. Проведем прямую через точки A = (x₁,f(x₁)) и B = (x₂,f(x₂)), лежащие на графике функции f. Уравнение этой прямой можно записать в виде

Обозначим правую часть этого уравнения через l(x), тогда оно запишется в виде

y = l(x).

    Определение 4. Функция f называется выпуклой вверх на интервале (a,b), если, каковы бы ни были точки x₁ и x₂, a < x₁ < x₂ < b, для любой точки x интервала (x₁,x₂) выполняется неравенство

    Если же для всех точек x (x₁,x₂) выполняется противоположное неравенство

то функция f называется выпуклой вниз на интервале (a,b).

Рис. 86

    Это означает, что любая точка хорды AB (т. е. отрезка прямой (15.15) с концами в точках A и B), например, в случае выпуклости вниз расположена не ниже точки графика функции f, соответствующей тому же значению аргумента (рис. 86).
    Заметим, что функция f выпукла вверх тогда и только тогда, когда функция -f выпукла вниз. 
    Если вместо неравенств (15.16) и (15.17) выполняются строгие неравенства l(x) < f(x) и l(x) > f(x), a < x₁ < x < x₂ < b, то функция f называется строго выпуклой вверх, соответственно строго выпуклой вниз на интервале (a,b). В этом случае любая точка хорды AB, кроме ее концов, лежит ниже (выше) соответствующей точки графика функции.
    Всякий интервал, на котором функция (строго) выпукла вверх, соответственно (строго) выпукла вниз, называется интервалом (строгой) выпуклости вверх, соответственно вниз этой функции.

    Теорема 5. (достаточные условия строгой выпуклости). Если вторая производная функции отрицательна (положительна) во всех точках интервала, то функция строго выпукла вверх (соответственно строго выпукла вниз) на этом интервале.
Если a < x₁ < x < x₂ < b, то

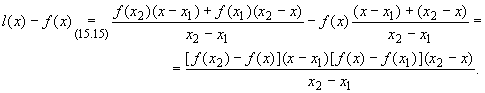
Применив к разностям значений функций, стоящим в квадратных скобках, теорему о среднем Лагранжа (п. 12.2), получим

где x₁ <  < x <  < x₂. Применим теперь теорему о среднем Лагранжа к разности значений производной
f'() - f'(); тогда будем иметь

Здесь знак правой части равенства совпадает со знаком f"() (все остальные сомножители положительны). Поэтому если f" < 0 на (a,b), то  l(x) < f(x), т. е. функция f строго выпукла вверх; если же f" > 0 на (a,b), то  l(x) > f(x), т. е. функция f строго выпукла вниз. 
    Отметим, что условие постоянства знака второй производной, являясь достаточным условием строгой выпуклости вверх или вниз, не является необходимым: на интервалах строгой выпуклости вверх или вниз вторая производная может обращаться в нуль. Например, функция y = x⁴ строго выпукла вниз на всей числовой прямой, однако ее вторая производная y" = 12x² обращается в нуль при x = 0.
    Замечание 4. Из доказательства теоремы 5 видно, что если условие положительности второй производной на интервале заменить условием ее неотрицательности, то функция будет выпукла вниз на этом интервале. Соответственно, если вторая производная неположительна на интервале, то функция выпукла вверх на этом интервале.
    Покажем, что расположение графика дважды дифференцируемой функции относительно касательной к этому графику также зависит от знака второй производной.
    Теорема 6. Пусть функция f имеет во всех точках x интервала (a,b) положительную (отрицательную) вторую производную f"(x) > 0 (соответственно f"(x) > 0). Тогда, какова бы ни была точка x₀ (a,b), все точки (x,f(x)), x (a,b) графика функции f лежат выше (соответственно ниже) касательной, проведенной к нему в точке (x₀,f(x₀)), кроме самой этой точки, которая лежит на касательной.
Если у функции f существует вторая производная в точке x₀, то в этой точке существует конечная первая производная, а следовательно, график функции имеет в точке (x₀,f(x₀)) наклонную касательную

Обозначим правую часть этого уравнения через L(x), тогда

f(x) - L(x)[ f(x) - f(x₀)] - f'(x₀)(x - x₀).

Применив к разности f(x) - f(x₀) теорему о среднем Лагранжа, получим

f(x) - L(x) = f'()(x - x₀) - f'(x₀)(x - x₀) = [f'() - f'(x₀)](x - x₀),

где a < x₀ < b, a < x < b а лежит между x₀ и x.
    Применив еще раз теорему Лагранжа, но уже к разности производных f'() - f'(x₀), будем иметь

где точка лежит между и x₀. Поскольку точка лежит между точками x и x₀, то точки и x расположены по одну сторону от точки x₀, и поэтому ( - x₀)(x - x₀) > 0. В силу этого знак разности f(x) - L(x) при xx₀ совпадает со знаком второй производной f"(). Следовательно, если на интервале (a,b) вторая производная положительна, то f(x) > L(x), т. е. график функции f лежит над касательной, а если вторая производная отрицательна, то f(x) < L(x), т. е. график функции лежит под касательной y = L(x), x (a,b), xx₀. 

    Определение 5. Пусть функция f дифференцируема при x = x₀ и пусть y = L(x) - уравнение наклонной касательной к графику функции f в точке (x₀,f(x₀)) (см. (15.18)). Если разность f(x) - L(x) меняет знак при переходе через точку x₀, то x₀ называется точкой перегиба функции f.
    Если x₀ - точка перегиба функции, то точка (x₀,f(x₀)) называется точкой перегиба графика функции f . В точке (x₀,f(x₀)) график функции f переходит с одной стороны наклонной касательной (15.18) на другую сторону (рис. 87).
    Пример. Рассмотрим функцию f(x) = x³. Поскольку f"(x) = 6x, то f"(x) < 0 для всех x < 0  и f"(x) > 0 для всех x > 0. Следовательно (теорема 5), функция f(x) = x³ выпукла вверх на бесконечном интервале (-,0) и выпукла вниз на (0,+) (см. рис. 82). Уравнение касательной к ее графику в точке (0,0) имеет вид y = 0. Поэтому поскольку при x < 0 выполняется неравенство f(x) < 0, а при x > 0 - неравенство f"(x) > 0, то точка x = 0 является точкой перегиба функции f(x) = x³.
    Теорема 7 (необходимое условие точки перегиба). Если в точке перегиба функции существует вторая производная, то она равна нулю.
    Действительно, пусть функция f имеет в точке x₀ вторую производную и, как и выше, y = L(x) - уравнение касательной к графику функции f в точке (x₀,f(x₀)), т. e.

L(x) f(x₀) + f'(x₀)(x - x₀).

Тогда в силу формулы Тейлора

f(x) - L(x) = f(x₀) + f'(x₀)(x - x₀) + f"(x₀)(x - x₀)²/2 + o((x - x₀)²) - L(x) =  f"(x₀)(x - x₀)²/2 + o((x - x₀)²), 
xx₀.

    Если бы  f"(x₀)0, то знак разности f(x) - L(x) в некоторой окрестности точки x₀ совпадал бы со знаком числа f"(x₀). В этом случае разность f(x) - L(x) не меняла бы знака в точке x₀ и, следовательно, эта точка не была бы точкой перегиба. Итак, если x₀ - точка перегиба функции f, то f"(x₀) = 0. 
    Теорема 8 (первое достаточное условие точек перегиба). Если функция f дифференцируема в точке x₀, дважды дифференцируема в некоторой проколотой окрестности этой точки и ее вторая производная меняет знак при переходе аргумента через точку x₀, то x₀ является точкой перегиба функции f.
    Действительно, запишем, как и выше, уравнение касательной
(15.18) к графику функции f в точке (x₀,f(x₀)) в виде y = L(x). При доказательстве теоремы 6 было показано (см. (15.19)), что

f(x) - L(x) = f"()( - x₀)(x - x₀),

где точки , и x лежат по одну сторону от точки x₀, и, следовательно, всегда

( - x₀)(x - x₀) > 0,    xx₀,

кроме того, когда точка x переходит с одной стороны от точки x₀ на другую, то то же происходит и с точкой . В силу этого разность f(x) - L(x), xx₀, имеет тот же знак, что и вторая производная f"(), и так как по условию эта производная в точке x₀ меняет знак, то меняет знак в этой точке и разность f(x) - L(x). Это и означает, что x₀ является точкой перегиба. 
    Теорема 9 (второе достаточное условие точек перегиба). Если в некоторой точке вторая производная функция равна нулю, а третья не равна нулю, то эта точка является точкой перегиба.
Пусть f"(x₀) = 0, f'"(x₀)  0. Согласно формуле Тейлора и в силу условия f"(x₀) = 0 имеем

f(x) = f(x₀) + f'(x₀)(x - x₀) +  f'"(x₀)(x - x₀)³/3! + o((x - x₀)³),      xx₀.

Отсюда, применив обозначение L(x) = f(x₀) + f'(x₀)(x - x₀) (y = L(x)) - уравнение касательной к графику функции f(x) в точке (x₀,f(x₀))), получим

f(x) - L(x) = f'"(x₀)(x - x₀)³/3! + o((x - x₀)³),      xx₀.

Отсюда следует, что в некоторой окрестности точки x₀ разность f(x) - L(x), т. е. разность ординат графика функции и касательной к нему, при xx₀ имеет тот же знак, что f'"(x₀)(x - x₀)³/3!, а следовательно, меняет его при переходе через точку x₀ (разность x - x₀ возводится в нечетную степень). Это и означает, что x₀ является точкой перегиба функции f. 

Локальные экстремумы функций  Оглавление  Асимптоты