Определение 3. Предел
Если положить
Пусть векторная функция r(t)
задана в некоторой окрестности точки t0;
тогда соотношение ![]() определено в соответствующей проколотой
окрестности точки t0.
определено в соответствующей проколотой
окрестности точки t0.
Определение 3. Предел ![]()
![]() (если он, конечно, существует) называется производной
векторной функции r(t) в точке t0
и обозначается r'(t0) или
(если он, конечно, существует) называется производной
векторной функции r(t) в точке t0
и обозначается r'(t0) или ![]() (t0)
(t0)
Если положить ![]() t = t - t0,
t = t - t0,
![]() r = r(t) - r(t0) = r(t0
+
r = r(t) - r(t0) = r(t0
+ ![]() t) - r(t0),
то
t) - r(t0),
то
|
(16.17) |
Пусть r(t) = (x(t), y(t), z(t)). Так как
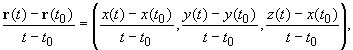
то в силу (16.9), (16.10) для того, чтобы векторная функция r(t) = (x(t), y(t), z(t)) имела производную в точке t0, необходимо и достаточно, чтобы ее координаты x(t), y(t), z(t) имели производные в точке t0, причем в этом случае
r'(t) = (x'(t0), y'(t0), z'(t0)). |
(16.18) |
Производную r'(t)
вектор-функции r(t) называют также скоростью
изменения вектора r(t)
относительно параметра t. В случае когда
длина вектора r(t) не меняется,
производная r'(t) называется
также и скоростью вращения вектора r(t),
а ее абсолютная величина - численным
значением скорости его вращения.
Замечание 1. По аналогии со
случаем скалярных функций векторную функцию ![]() (t), t
(t), t ![]() X, называют бесконечно
малой по сравнению со скалярной функцией
X, называют бесконечно
малой по сравнению со скалярной функцией ![]() (t), t
(t), t ![]() X, при t
X, при t![]() t0 и пишут
t0 и пишут ![]() (t) = o(
(t) = o(![]() (t)), t
(t)), t![]() t0,
если существует векторная функция
t0,
если существует векторная функция ![]() (t), определенная на том же
множестве X, что и функции
(t), определенная на том же
множестве X, что и функции ![]() (t),
(t),
![]() (t), такая, что в
некоторой окрестности точки t = t0
имеет место равенство
(t), такая, что в
некоторой окрестности точки t = t0
имеет место равенство ![]() (t) =
(t) = ![]() (t)
(t)![]() (t), t
(t), t ![]() X, и
X, и
![]()
![]() (t) = 0.
(t) = 0.
Как и для скалярных функций, если t0
![]() X, то
функция
X, то
функция ![]() (t) непрерывна в
точке t0, и потому
(t) непрерывна в
точке t0, и потому ![]() (t0)
= 0.
(t0)
= 0.
Замечание 2. Вектор-функция
аргумента t называется линейной, если
она имеет вид at + b,
где a и b - какие-либо два
фиксированных вектора.
После этих вводных замечаний можно
определить понятие дифференцируемости и
дифференциала вектор-функции.
Определение 4. Вектор-функция r(t),
заданная в некоторой окрестности точки t0,
называется дифференцируемой при t = t0,
если ее приращение ![]() r
= r(t0 +
r
= r(t0 + ![]() t) - r(t0) в точке t0
представимо в виде
t) - r(t0) в точке t0
представимо в виде
|
(16.19) |
При этом линейная вектор-функция a![]() t приращения
аргумента
t приращения
аргумента ![]() t
называется дифференциалом функции r(t)
в точке t0 и обозначается через dr,
т. е. dr = a
t
называется дифференциалом функции r(t)
в точке t0 и обозначается через dr,
т. е. dr = a![]() t.
t.
Таким образом,
|
(16.20) |
Здесь функция o(![]() t) определена при
t) определена при ![]() t = 0; в этой точке она равна
нулю:
t = 0; в этой точке она равна
нулю:
![]()
Следовательно, если представить эту функцию o(![]() t) в виде (см.
замечание 1) o(
t) в виде (см.
замечание 1) o(![]() t) =
t) = ![]() (
(![]() t)
t)![]() t, то функция
t, то функция
![]() (
(![]() t)
также будет определена при
t)
также будет определена при ![]() t = 0, а поэтому, как было отмечено
выше, в этом случае
t = 0, а поэтому, как было отмечено
выше, в этом случае ![]() (0) = 0.
Благодаря этому здесь предел
(0) = 0.
Благодаря этому здесь предел
|
(16.21) |
рассматривается не по проколотой, а по целой
окрестности точки ![]() t
= 0.
t
= 0.
Формулу (16.19) теперь можно записать в
виде
|
(16.22) |
Докажем несколько простых
утверждений о дифференцируемых векторных
функциях, аналогичных соответствующим
утверждениям для скалярных функций.
I. Если векторная функция r(t)
дифференцируема в некоторой точке, то она и
непрерывна в этой точке.
![]()
![]()
![]()
II. Если векторная функция r(t) дифференцируема в точке t0, то она имеет в этой точке производную и
r'(t) = a,
где вектор a определяется формулой (16.19).
![]()
![]()
![]()
Верным является и обратное
утверждение.
III. Векторная функция, имеющая в
некоторой точке производную, дифференцируема
в этой точке.
![]() Если
существует производная r'(t0)
=
Если
существует производная r'(t0)
= ![]() (
(![]() r/
r/![]() t)
и, следовательно, r'(t0) =
t)
и, следовательно, r'(t0) = ![]() r/
r/![]() t +
t + ![]() (
(![]() t),
t), ![]() t
t![]() 0, где
0, где
![]() , то
, то
![]() r = r'(t0)
+
r = r'(t0)
+ ![]() (
(![]() t)
t)![]() t.
t.
Полагая ![]() (0) = 0,
получим, что условие
(0) = 0,
получим, что условие ![]()
![]() (t) выполняется и без
ограничения
(t) выполняется и без
ограничения ![]() t
t![]() 0.
0.
Таким образом, имеет место (16.22) при a =
r'(t0), т. е. функция r(t)
дифференцируема в точке t0 и
dr(t0) = r'(t0)![]() t.
t. ![]()
По определению считается, что dt ![]()
![]() t. Поэтому (опуская для простоты
обозначения аргумента) имеем dr = r'dt,
или r' = dr/dt.
t. Поэтому (опуская для простоты
обозначения аргумента) имеем dr = r'dt,
или r' = dr/dt.
IV. Если t = t(![]() ) -
дифференцируемая в точке
) -
дифференцируемая в точке ![]() 0
числовая функция, а r(t) -
дифференцируемая в точке
0
числовая функция, а r(t) -
дифференцируемая в точке
t0 = t(![]() 0)
векторная функция, то сложная функция r(t(
0)
векторная функция, то сложная функция r(t(![]() )) дифференцируема
в точке
)) дифференцируема
в точке ![]() 0 и
0 и
![]()
или, короче
|
(16.23) |
![]() Из соотношения (16.22)
имеем при
Из соотношения (16.22)
имеем при ![]()
![]()
![]() 0
0
|
(16.24) |
По условию функция t = t(![]() ) дифференцируема в точке
) дифференцируема в точке ![]() 0, т. е. существует
конечный предел
0, т. е. существует
конечный предел
|
(16.25) |
Отсюда следует, что эта функция в рассматриваемой точке непрерывна:
![]()
![]() t = 0.
t = 0.
Отсюда и из условия (16.21) вытекает, что ![]()
![]() (
(![]() t) = 0.
t) = 0.
Из всего сказанного следует, что при ![]()
![]()
![]() 0 правая
часть равенства (16.24), а следовательно, и его левая
часть имеют конечные пределы. Это означает, что в
точке
0 правая
часть равенства (16.24), а следовательно, и его левая
часть имеют конечные пределы. Это означает, что в
точке ![]() 0 существует
производная
0 существует
производная ![]() и что
и что
![]()
Из формулы (16.23) аналогично случаю
скалярных функций вытекает инвариантность
записи дифференциала векторной функции: как для
зависимой переменной t, так и для
независимой ![]() имеем
имеем
dr = r'tdt,
dr = |
(16.26) |
т. е. чтобы из второй формулы получить первую,
надо подставить во вторую формулу ![]() и заметить, что
и заметить, что ![]() .
.
V. Для производных вектор-функций
имеют место формулы, аналогичные
соответствующим формулам для скалярных функций:
(r1 + r2)' =
r'1 + r'2,
(fr)' = f'r + fr',
(r1r2)' = r'1r2
+ r1r'2,
(r1 x r2)'
= r'1 x
r2 + r1 x
r'2.
Здесь все производные берутся в
одной и той же точке. Предполагается, что
производные, стоящие в правой части каждого
равенства, существуют, и утверждается, что в этом
случае существуют и производные, находящиеся в
левых частях равенств.
![]() Доказываются эти
формулы аналогично скалярному случаю. Докажем,
например, последнюю из них.
Доказываются эти
формулы аналогично скалярному случаю. Докажем,
например, последнюю из них.
Заметив, что r1(t0
+ ![]() t) = r1(t0)
+
t) = r1(t0)
+ ![]() r1, r2(t0
+
r1, r2(t0
+ ![]() t) = r2(t0)
+
t) = r2(t0)
+ ![]() r2,
получим
r2,
получим
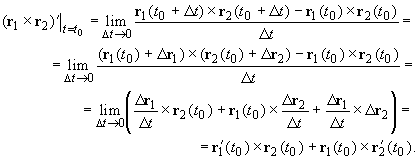
![]()
Для дальнейшего нам будет полезна
следующая
Лемма. Если вектор-функция r(t)
дифференцируема в точке t0 и все
векторы r(t) имеют одну и ту же
длину в некоторой окрестности точки t0,
то производная r'(t0)
ортогональна вектору r(t0):
![]() Действительно, если в
указанной окрестности |r(t)| = c,
где c - константа, то |r|2 = c2,
т. е. r2 = c.
Дифференцируя это равенство, получим 2rr' = 0,
что равносильно равенству (16.27).
Действительно, если в
указанной окрестности |r(t)| = c,
где c - константа, то |r|2 = c2,
т. е. r2 = c.
Дифференцируя это равенство, получим 2rr' = 0,
что равносильно равенству (16.27). ![]()
Утверждение леммы содержательно лишь
в случае, когда r'(t0) ![]() 0 (если r'(t0) = 0,
то условие (16.27), очевидно, выполняется и без
условия постоянства длины вектора r(t)).
В этом случае физический смысл формулы (16.27)
состоит в том, что у материальной точки,
движущейся по поверхности шара (r(t) -
радиус-вектор этой точки, t - время
движения, c - радиус указанного шара),
скорость v = dr/dt всегда
направлена при v
0 (если r'(t0) = 0,
то условие (16.27), очевидно, выполняется и без
условия постоянства длины вектора r(t)).
В этом случае физический смысл формулы (16.27)
состоит в том, что у материальной точки,
движущейся по поверхности шара (r(t) -
радиус-вектор этой точки, t - время
движения, c - радиус указанного шара),
скорость v = dr/dt всегда
направлена при v![]() 0 по касательной к поверхности шара,
т. е. перпендикулярно радиусу шара.
0 по касательной к поверхности шара,
т. е. перпендикулярно радиусу шара.
Производные высших порядков для
вектор-функции определяются по индукции: если у
вектор-функции r(t) в некоторой
окрестности точки t0 задана
производная r(n)(t)
порядка n, n = 0, 1, 2, ... (r(0)(t)![]() r(t)), то
производная порядка n + 1 в этой точке
(если эта производная, конечно, существует)
определяется по формуле
r(t)), то
производная порядка n + 1 в этой точке
(если эта производная, конечно, существует)
определяется по формуле
![]()
Если векторная функция имеет в
некоторой точке n производных, то говорят
также, что она в этой точке n раз
дифференцируема. Можно и для векторных функций
по аналогии со скалярными ввести понятие
дифференциалов высших порядков, но не будем на
этом останавливаться.
Если векторная функция r(t) = (x(t),
y(t), z(t)) n раз
дифференцируема в точке t = t0, то в
некоторой окрестности этой точки для функции r(t)
имеет место формула
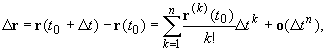
![]() t
t![]() 0.
0.
называемая по аналогии со скалярным случаем формулой
Тейлора (порядка n) функции r(t)
с остаточным членом в виде Пеано. Эта формула
непосредственно следует из разложений по
формуле Тейлора координат x(t), y(t),
z(t) векторной функции r(t).
Из всего сказанного видно, что
рассмотренные определения и утверждения для
векторных функций получаются перенесением
соответствующих определений и утверждений из
теории скалярных функций.
Замечание 3. Следует, однако,
иметь в виду, что не все, что справедливо для
скалярных функций, имеет прямой аналог в
векторном случае. Это относится, например, к
теореме Ролля, а следовательно, и к теореме
Лагранжа, частным случаем которой является
теорема Ролля.
В самом деле, рассмотрим
дифференцируемую векторную функцию r(t) = (cos
t, sin t), 0 < t < 2![]() (третья координата функции r(t) -
тождественный нуль). Поскольку r'(t) = (-sin t,
cos t), то |r'(t)| = (sin2 t + cos2
t)1/2 = 1 при любом t
(третья координата функции r(t) -
тождественный нуль). Поскольку r'(t) = (-sin t,
cos t), то |r'(t)| = (sin2 t + cos2
t)1/2 = 1 при любом t ![]() [0,2
[0,2![]() ],
и, следовательно, не существует такой точки
],
и, следовательно, не существует такой точки ![]() , для которой было бы r'(
, для которой было бы r'(![]() ) = 0, несмотря
на то, что r(0) = r(2
) = 0, несмотря
на то, что r(0) = r(2![]() ).
).
Для векторных функций вместо прямого
аналога теоремы Лагранжа можно доказать
нижеследующую теорему 1.
Ее формулировке и доказательству
предпошлем два замечания.
Замечание 4. Если вектор x
ненулевой и x0 - единичный
вектор в направлении вектора x, т. е. x0 = x/|x|,
то
|x| = xx0. |
(16.28) |
В самом деле, согласно определению скалярного произведения
xx0 = |x||x0|cos |
(16.29) |
Здесь по условию |x0| = 1, а ![]() = 0 и, следовательно, cos
= 0 и, следовательно, cos![]() = 1, т. е. равенство (16.29)
превращается в равенство (16.28).
= 1, т. е. равенство (16.29)
превращается в равенство (16.28).
Замечание 5. Для любых векторов x
и y имеет место неравенство
xy < |x||y|. |
(16.30) |
![]() Действительно,
Действительно,
xy < ||x||y|cos![]() | = |x||y||cos
| = |x||y||cos![]() | < |x||y|.
| < |x||y|.
![]()
Теорема 1. Если
вектор-функция r(t) непрерывна
на отрезке [a,b] и дифференцируема
внутри него, то существует такая точка ![]()
![]() (a,b), что
(a,b), что
|r(b) - r(a)|
< |r( |
(16.31) |
![]() Если r(a) = r(b),
то неравенство (16.31) справедливо при любом выборе
точки
Если r(a) = r(b),
то неравенство (16.31) справедливо при любом выборе
точки ![]()
![]() (a,b), так как его левая
часть обращается в нуль.
(a,b), так как его левая
часть обращается в нуль.
Пусть r(a) ![]() r(b) и,
следовательно, r(b) - r(a)
r(b) и,
следовательно, r(b) - r(a)
![]() 0. Если e -
единичный вектор в направлении вектора r(b) - r(a),
то согласно замечанию 4
0. Если e -
единичный вектор в направлении вектора r(b) - r(a),
то согласно замечанию 4
|r(b) - r(a)| = (r(b) - r(a))e = r(b)e - r(a)e,
т. е. получилась разность значений скалярной функции
f(t) |
(16.32) |
на концах отрезка [a,b]:
|r(b) - r(a)| = f(b) - f(a). |
(16.33) |
Из формулы (16.32) следует, что функция f
непрерывна на отрезке [a,b] и
дифференцируема во всех его внутренних точках,
ибо согласно условиям теоремы этими свойствами
обладает функция r(t). Поэтому в силу
формулы конечных приращений Лагранжа существует
такая точка ![]()
![]() (a,b), что f(b)
- f(a) = f'(
(a,b), что f(b)
- f(a) = f'(![]() )(b
- a). Но согласно правилу
дифференцирования скалярного произведения
имеем f'(t) = r(t)e,
вследствие чего
)(b
- a). Но согласно правилу
дифференцирования скалярного произведения
имеем f'(t) = r(t)e,
вследствие чего
f(b) - f(a) = r'( |
(16.34) |
Поскольку в силу неравенства (16.30) имеет место неравенство
r'( |
(16.35) |
то
![]()
Неравенство (16.31) доказано. ![]()