17.1. Понятие кривой

    Рассмотрим отображение некоторого отрезка [a,b] числовой прямой R в пространство R³, т. е. такое отображение, которое каждой точке t [a,b] ставит в соответствие точку M(t) пространства R³. Если в пространстве R³ задана прямоугольная декартова система координат x, y, z, то между точками пространства R³ и тройками чисел x, y, z имеется взаимно однозначное соответствие, а поэтому задание отображения M(t) R³ t [a,b], равносильно заданию трех числовых функций (называемых координатными) x(t), y(t), z(t),  где x(t), y(t), и z(t) являются координатами точки M(t).
    Отображение M(t) R³, t [a,b], называется непрерывным на отрезке [a,b], если на этом отрезке непрерывны все его координатные функции x(t), y(t), z(t).
    Определение 1. Непрерывное отображение отрезка в пространство называется кривой.
    Кривые будем обозначать большими греческими буквами Г, . Если M(t), a < t < b, - непрерывное отображение какого-либо отрезка [a,b] в пространство, т. е. кривая Г, то будем писать

или

где x(t), y(t), z(t), - координатные функции отображения M(t),   a < t < b.
    Координатные функции x(t), y(t), z(t),  отображения M(t), t [a,b], однозначно задают вектор-функцию r(t), координатами которой они являются:

    Эта вектор-функция называется векторным представлением кривой (17.1). Если начало вектора r(t) поместить в начало координат, то его концом будет точка M(t). При задании кривой Г ее векторным представлением (17.3) пишут

    Множество точек пространства R³, на которое отображение (17.1) отображает отрезок [a,b], называется носителем кривой Г.
    Иногда там, где это не может привести к недоразумению, носитель кривой называется также кривой.
    Если O - начало координат в пространстве R³, то конец радиус-вектора (t) при изменении параметра t на отрезке [a,b] пробегает носитель кривой Г. В дальнейшем, когда будут рассматриваться векторные представления (17.4) кривой Г, всегда будет предполагаться, что вектор r(t) является радиус-вектором с началом в начале координат, т. е. что r(t) = (t).
    Переменная t называется параметром на кривой Г. Всякая строго монотонная непрерывная на некотором отрезке [,] функция

отображающая отрезок [,] на отрезок [a,b], для которой, следовательно, в случае ее строгого возрастания выполняется условие

t() = a,     t() = b,

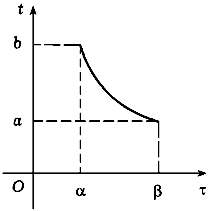
а в случае строгого убывания - условие

t() = b,     t() = a

(рис. 91),называется преобразованием параметра t кривой (17.1) (или, полнее, преобразованием параметра t к параметру ). Обратная к функции t = t() функция = (t) является, очевидно, преобразованием параметра для кривой {M(t()); < < }.

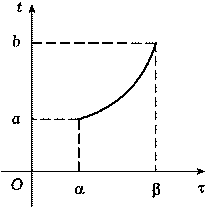Рис. 91

    При преобразовании параметра t = t() из равенства M(t) = M(t()); < < , следует, что исходная кривая и кривая, получающаяся из нее с помощью преобразования параметра, имеют один и тот же носитель.
    Если t = t(), < < , - преобразование параметра, то кривые {M(t); a < t < b} и{M(t()); < < } часто называют одной и той же кривой с разными параметризациями.
    Если координатные функции x(t), y(t), z(t) отображения (17.1) n раз дифференцируемы или n раз непрерывно дифференцируемы (т. е. имеют n непрерывных производных) на отрезке [a,b], то кривая Г называется n раз дифференцируемой или, соответственно, n раз непрерывно дифференцируемой кривой.
    Преобразованиями параметра n раз ( непрерывно) дифференцируемой кривой называются такие n раз (непрерывно) дифференцируемые строго монотонные функции (17.5), у которых во всех точках отрезка [,]  их производная не равна нулю:

t'()0,   [,]

Это условие нужно для того, чтобы обратная функция = (t), a < t < b, была также преобразованием параметра кривой M(t(), < < (см. формулы для производной обратной функции в п. 10.6).
    Для того чтобы кривая Г была n раз дифференцируема (соответственно n раз непрерывно дифференцируема,  = 1, 2, ...), необходимо и достаточно, чтобы ее векторное представление (17.2) было n раз дифференцируемо (соответственно n раз непрерывно дифференцируемо). Это следует из того, что непрерывность (дифференцируемость) векторной функции равносильна непрерывности (дифференцируемости) ее координат (п. 16.2).
    Точка носителя кривой Г, в которую при отображении (17.1) отображаются по крайней мере две разные точки отрезка [a,b], называется кратной точкой носителя этой кривой или точкой самопересечений кривой. Если кратная точка носителя кривой Г имеет в точности n прообразов при отображении M(t), a < t < b, то
эта точка называется n-кратной.
    Если носитель кривой Г не имеет кратных точек, т. е. отображение (17.1) взаимно однозначно отображает отрезок [a,b] в пространство R³, то кривая Г называется просто дугой.
   Точкой кривой (17.1) называется пара (M,t), где M = M(t) R³, a t [a,b]. Точка M R³ называется носителем точки (M,t).
    Носитель точки кривой там, где это не может привести к недоразумению, называется иногда также точкой кривой.
    Если M₀ = M(a), а M₁ = M(b), то точка (M₀,a) называется началом кривой Г, а точка (M₁,b) - ее концом (впрочем, иногда обе точки (M₀,a) и (M₁,b) называют концами кривой Г).
    Если носители начала и конца кривой Г совпадают: M(a) = M(b), то кривая Г называется замкнутой.
    Если у носителя замкнутой кривой нет других кратных точек, кроме носителя ее начала и конца, который является двукратной точкой, то кривая Г называется простым замкнутым контуром.
    Там, где это не может привести к недоразумениям (например, для простых дуг), точка (M,t) кривой Г часто обозначается M(t), т. е. тем же символом, что и носитель указанной точки.
    Если t₁ [a,b], t₂ [a,b], t₁ < t₂, то кривая {M(t); t₁ < t < t₂} называется частью кривой (17.1) или ее дугой

с началом в точке M(t₁) и концом в M(t₂).
    Если носитель кривой Г лежит в некоторой плоскости, то эта кривая называется плоской.
    Примеры.
    1. Рассмотрим две замкнутые плоские кривые:

x = cos t,      y = sin t,      0 < t < 2,

(17.6)

и

x = cos t,      y = sin t,      0 < t < 4.

(17.7)

    Их носителями является одна и та же окружность x² + y² = 1, но это две разные кривые: у кривой (17.6) параметр t изменяется от 0 до 2, и эта окружность проходится один раз, а у кривой (17.7) параметр t изменяется от 0 до 4, и та же окружность проходится два раза.
    Носитель кривой (17.6) имеет только одну кратную точку - носитель начала и конца этой кривой. У носителя кривой (17.7) все точки кратные.
    2. Непрерывная на некотором отрезке [a,b] функция y = f(x), a < x < b, задает плоскую кривую x = t, y = f(t), a < b, являющуюся, очевидно, простой дугой. Ее носителем является график функции f, а параметром - переменная x. В этом случае пишут

Г = { y = f(x); a < x < b}

и говорят, что кривая Г имеет явное представление - функцию f.
    Упорядоченность точек отрезка [a,b] порождает с помощью отображения M(t), a < t < b, упорядоченность точек на кривой Г = {M(t); a < t < b}. Если t₁ < t₂, то точка M(t₁) кривой Г называется точкой, предшествующей точке M(t₂) этой кривой. Этот порядок точек называется ориентацией кривой, а кривая, на которой задана ориентация, называется ориентированной кривой.
    Порядок точек на кривой

называется противоположным порядку точек кривой  Г = {M(t); a < t < b} ( противоположной ориентацией кривой), а сама кривая (17.8) - кривой, ориентированной противоположно к данной кривой Г. Для ориентированной кривой преобразованием параметра называются только строго возрастающие функции - они не меняют порядок точек, в то время как строго убывающие меняют их порядок на противоположный.
    Замечание 1. Задания кривой Г в виде M(t), (x(t), y(t), z(t)) и r(t), a < t < b, называют ее параметрическими заданиями, а саму кривую Г называют также параметрически заданной непрерывной кривой.
    Замечание 2. Если для плоской кривой Г существует такая функция F(x,y), что координаты всех точек (x,y) носителя кривой Г удовлетворяют условию

то говорят, что уравнение (17.9) является неявным заданием кривой Г.
    Следует иметь в виду, что, вообще говоря, множество всех точек, удовлетворяющих уравнению вида (17.9), не является носителем некоторой кривой в определенном выше смысле даже для достаточно "хороших" функций F(x,y). Например, множество точек, координаты которых удовлетворяют уравнению

(x² + y²)(x² + y² - 1) = 0,

представляет собой окружность x² + y² = 1 и точку (0,0).
    Замечание 3. В случае кривых, лежащих на плоскости, иногда бывает удобно их задавать в полярных координатах , ( - полярный радиус точки плоскости, а  - угол, образованный им с полярной осью), которые связаны с декартовыми координатами x,y соотношениями

В полярных координатах кривая задается уравнениями вида

С помощью формул (17.10) задание кривой уравнением (17.11) сразу сводится к ее параметрическому заданию

x = ()cos,    y = ()sin,    < < ,

где за параметр взят полярный угол .
    Замечание 4. Отметим еще, что сформулированное определение кривой не охватывает все то, что интуитивно естественно отнести к понятию кривой, например, прямую линию, гиперболу, параболу и т. п. Чтобы охватить определением и подобные "кривые", следует рассмотреть отображения в пространство не только отрезков, но и других промежутков числовой оси: интервалов и полуинтервалов.

Производная и дифференциал векторной функции   Оглавление   Касательная к кривой