16.1. Предел и непрерывность векторной функции
В этом параграфе будут изучаться
функции, значениями которых являются векторы, а
аргументами - числа. Такие функции называют вектор-функциями
или векторными функциями (числового
аргумента). Они обозначаются жирным шрифтом: r(t),
или с помощью черты над значениями функции: 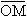 (t), t
(t), t  X, где X - некоторое
числовое множество.
X, где X - некоторое
числовое множество.
В этом определении в
зависимости от рассматриваемых задач под
векторами r(t) могут пониматься как
свободные векторы, так и векторы с закрепленными
началами. Если начала всех векторов закреплены в
одной и той же точке (обычно - начало
координат), то такие векторы называются радиус-векторами.
Если в трехмерном евклидовом
пространстве задана прямоугольная система
координат, то, как хорошо известно, каждому
вектору соответствует упорядоченная тройка
действительных чисел - его координат и,
наоборот, каждой упорядоченной тройке чисел
соответствует вектор, для которого числа,
входящие в эту тройку, являются его координатами.
Поэтому задание вектор-функции r(t), t
 X,
эквивалентно заданию трех скалярных, т. е.
числовых, функций x(t), y(t), z(t),
t
X,
эквивалентно заданию трех скалярных, т. е.
числовых, функций x(t), y(t), z(t),
t  X,
являющихся его координатами:
X,
являющихся его координатами:
r(t) = (x(t),
y(t), z(t)), t  X.
X.
Длина (абсолютная величина) всякого вектора a,
обозначается |a| скалярное произведение
векторов a и b - через ab
или (a,b), а векторное - через a x b или [a,b].
Определим понятия предела,
непрерывности, производной и дифференциала для
векторных функций.
Определение 1. Вектор a
называют пределом вектор-функции r(t),
t  X, при t
X, при t t0 (или в точке t =
t0) и пишут
t0 (или в точке t =
t0) и пишут
 r(t)
= a, r(t)
= a,
|
(16.1) |
если
 |r(t)
- a| = 0. |r(t)
- a| = 0.
|
(16.2) |
В этом определении |r(t) - a|
- числовая функция. Таким образом, понятие
предела векторной функции сводится к понятию
предела скалярной функции. Вспомнив определение
этого понятия, получим, что (16.1) означает, что
для любого  > 0
существет такое
> 0
существет такое  > 0,
что для всех
> 0,
что для всех
выполняется неравенство
|r(t) - a|
<  . . |
(16.4) |
Как и в случае скалярных функций,
будем предполагать, что t0 является
точкой прикосновения (конечной или бесконечно
удаленной) множества X. Если t0 -
конечная точка, то условие (16.3) можно записать в
виде
|t - t0| <  , t , t  X, X, |
(16.5) |
а если t0 - одна из бесконечно
удаленных точек 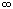 ,
+
,
+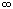 или -
или -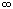 , то
соответственно в одном из следующих трех видов:
, то
соответственно в одном из следующих трех видов:
|t| > 1/ , t > 1/ , t > 1/ , t
< -1/ , t
< -1/ , , |
(16.6) |
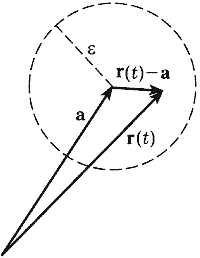
Рис. 90
|
и, конечно, всегда t  X.
X.
Если начало всех векторов r(t)
поместить в одну точку (например, в начало
координат), то условие (16.4) будет означать, что
концы всех векторов r(t) при t  X
X  U(t0,
U(t0, ) лежат в шаре радиуса
) лежат в шаре радиуса  с центром в конце
вектора a (рис. 90).
с центром в конце
вектора a (рис. 90).
Если r(t) = (x(t), y(t),
z(t)) и a = (a1,a2,a3),
то
|r(t) - a| =
{[x(t) - a1]2 + [x(t) - a2]2 + [x(t) - a3]2}1/2 |
(16.7) |
и, следовательно
|x(t) - a1|
< |r(t) - a|,
|y(t) - a2| < |r(t)
- a|,
|z(t) - a3| < |r(t)
- a|. |
(16.8) |
Поэтому предел
 r(t)
= a r(t)
= a
|
(16.9) |
векторной функции r(t) существует
в том и только том случае, когда существуют
пределы ее координат
 x(t) = a1, x(t) = a1,
 y(t) = a2, y(t) = a2,
 z(t) = a3. z(t) = a3.
|
(16.10) |
Действительно, в силу соотношений
(16.7) и (16.8) для того, чтобы выполнялось условие (16.2),
необходимо и достаточно, чтобы
 |x(t) - a1|
= 0,
|x(t) - a1|
= 0,  |y(t) - a2|
= 0,
|y(t) - a2|
= 0,  |z(t) - a3|
= 0.
|z(t) - a3|
= 0.
Аналогично случаю числовых функций,
если t0  X и на множестве X существует предел
X и на множестве X существует предел  r(t), то этот
предел равен значению функции r(t) в
точке t0:
r(t), то этот
предел равен значению функции r(t) в
точке t0:  r(t)
= r(t0).
r(t)
= r(t0).
Определение 2. Если t0 -
конечная точка и для функции r(t), t
 X, имеет
место равенство
X, имеет
место равенство
 r(t)
= r(t0), r(t)
= r(t0),
|
(16.11) |
то эта функция называется непрерывной в точке
t0.
Как и в случае скалярных функций,
условие (16.11) выполняется тогда и только тогда,
когда существует  r(t)
и t0
r(t)
и t0  X.
X.
Если положить 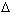 t = t - t0,
t = t - t0,
 r = r(t0
+
r = r(t0
+  t) - r(t0),
то условие (16.11) примет вид
t) - r(t0),
то условие (16.11) примет вид 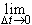
 r = 0.
r = 0.
Из эквивалентности условий (16.9) и (16.10)
следует, что векторная функция непрерывна в
некоторой точке тогда и только тогда, когда в
этой точке непрерывны все ее координатные
функции.
Отметим основные свойства пределов
векторных функций.
1o. Если  r(t) = a, то
r(t) = a, то  |r(t)| = |a|.
Это непосредственно следует из неравенства ||r - ||a|| < |r - a|.
|r(t)| = |a|.
Это непосредственно следует из неравенства ||r - ||a|| < |r - a|.
Геометрический смысл этого неравенства состоит
в том, что разность длин двух сторон треугольника
не превышает длины его третьей стороны.
2o.  [r1(t)
+ r2(t)] =
[r1(t)
+ r2(t)] =  r1(t) +
r1(t) + r2(t).
r2(t).
3o.  f(t)r1(t)
=
f(t)r1(t)
=  f(t)
f(t) r1(t) ( f(t) -
скалярная функция).
r1(t) ( f(t) -
скалярная функция).
4o.  r1(t)r2(t)
=
r1(t)r2(t)
=  r1(t)
r1(t) r2(t).
r2(t).
5o.  r1(t)
x r2(t) =
r1(t)
x r2(t) =  r1(t) x
r1(t) x r2(t).
r2(t).
В свойствах 2o-5o все
рассматриваемые функции определены на некотором
множестве x  R; предполагается, что все
пределы, входящие в правые части равенств,
существуют, и утверждается, что существуют
пределы, стоящие в левых частях, причем имеют
место написанные формулы. Все эти свойства
доказываются методом, аналогичным методу,
которым доказывались свойства пределов
скалярных функций в п. 6.7.
R; предполагается, что все
пределы, входящие в правые части равенств,
существуют, и утверждается, что существуют
пределы, стоящие в левых частях, причем имеют
место написанные формулы. Все эти свойства
доказываются методом, аналогичным методу,
которым доказывались свойства пределов
скалярных функций в п. 6.7.
 Докажем в качестве
примера свойство 5o. Заметим
предварительно, что для любых двух векторов p
и q справедливо неравенство
Докажем в качестве
примера свойство 5o. Заметим
предварительно, что для любых двух векторов p
и q справедливо неравенство
|p x
q| = |p||q|sin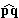 < |p||q|. < |p||q|. |
(16.12) |
Поэтому если p = p(t), q = q(t),
причем  |p(t)| =
0, а |q(t)| - ограниченная функция,
то в силу неравенства (16.12)
|p(t)| =
0, а |q(t)| - ограниченная функция,
то в силу неравенства (16.12)
 |p
x q| = 0. |p
x q| = 0.
|
(16.13) |
Пусть теперь  r1(t)
= a,
r1(t)
= a,  r2(t)
= b. Положим
r2(t)
= b. Положим
тогда, согласно (16.2),
Преобразуем произведение r1(t) x r1(t)
с помощью формул (16.14):
Здесь в силу (16.13)
 |a x
|a x 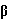 (t)| =
(t)| =  |
|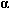 (t) x b|
=
(t) x b|
=  |
|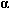 (t) x
(t) x 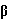 (t)| = 0,
(t)| = 0,
а так как
|a x 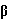 (t) +
(t) + 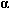 (t) x b
+
(t) x b
+ 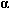 (t) x
(t) x 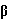 (t)| < |a x
(t)| < |a x 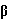 (t)| + |
(t)| + |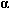 (t) x b| + |
(t) x b| + |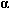 (t) x
(t) x 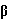 (t)|,
(t)|,
то  |a x
|a x
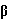 (t) +
(t) + 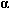 (t) x b
+
(t) x b
+ 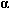 (t) x
(t) x 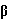 (t)| = 0.
(t)| = 0.
Отсюда в силу (16.16) имеем  |r1(t) x r1(t)
- a x b| = 0,
что согласно определению 1
(см. (16.2)) и доказывает свойство 5o.
|r1(t) x r1(t)
- a x b| = 0,
что согласно определению 1
(см. (16.2)) и доказывает свойство 5o. 
Из свойств пределов векторных функций
и определения их непрерывности следует, что
сумма, скалярное и векторное произведения
векторных функций, а также произведение
скалярных функций на векторные непрерывны в
некоторой точке, если в этой точке непрерывны все
слагаемые или соответственно сомножители.
Построение графиков
функций Оглавление Производная и дифференциал векторной
функции
