Будут изложены методы, с помощью которых можно вычислить, т. е. выразить через элементарные функции, интегралы от рациональных дробей.
Рассмотрим сначала элементарные дроби вида
n > 1, то
В этом параграфе будут
рассматриваться рациональные дроби, у которых в
числителе и знаменателе стоят многочлены с
действительными коэффициентами. Будет всегда
предполагаться, что коэффициент у старшего члена
многочлена, стоящего в знаменателе, равен 1
(этого, очевидно, всегда можно достичь, поделив
числитель и знаменатель дроби на указанный
коэффициент).
Будут изложены методы, с помощью
которых можно вычислить, т. е. выразить через
элементарные функции, интегралы от рациональных
дробей.
Рассмотрим сначала элементарные дроби
вида ![]() . Если
. Если
n > 1, то
|
(20.1) |
Если n = 1, то
|
(20.2) |
Вычислим теперь интеграл от элементарной дроби вида
![]() p2/4 - q < 0,
n = 1, 2, ...
p2/4 - q < 0,
n = 1, 2, ...
Заметив, что
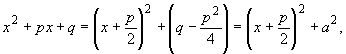
где a2 ![]() q - p2/4, и положив t = x + p/2,
будем иметь
q - p2/4, и положив t = x + p/2,
будем иметь
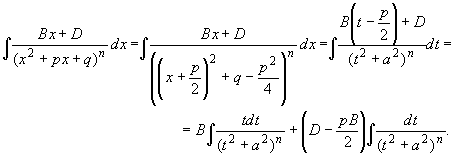
Таким образом, вычисление интеграла ![]() сводится к вычислению
интегралов, стоящих в правой части получившегося
равенства.
сводится к вычислению
интегралов, стоящих в правой части получившегося
равенства.
Если n = 1, то
|
(20.3) |
|
(20.4) |
Если же n > 1, то
|
(20.5) |
Для интеграла In ![]()
![]() , n > 1,
выведем с помощью интегрирования по частям
рекуррентную формулу, т. е. выразим In
через In+1:
, n > 1,
выведем с помощью интегрирования по частям
рекуррентную формулу, т. е. выразим In
через In+1:
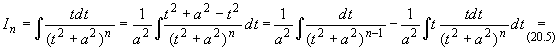
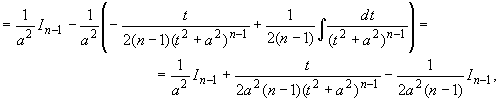
|
(20.6) |
Так как интеграл I1 уже вычислен (см.
(20.4)), по формуле (20.6) можно последовательно
вычислить I2, I3 и т. д.
Таким образом, интеграл от любой
элементарной дроби находится в явном виде и
является элементарной функцией.