21.2. Интегралы вида 

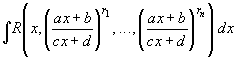
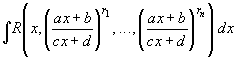
Рассмотрим интеграл .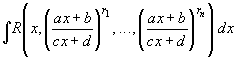

Будем предполагать, что числа r₁, ..., r_n рациональны и записаны с одним и тем же знаменателем:  r_i = p_i/m, m - натуральное число, p_i целые, i = 1, 2, ... n, и что определитель  не равен 0. Если бы = 0, то существовали бы такие числа , , что ² +²0 и  a +c = 0, b +d = 0, a тогда, например, при 0 имело бы место равенство

и, следовательно, функция 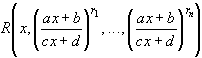 была бы просто рациональной функцией.
    Сделаем в рассматриваемом интеграле замену переменной

откуда

Здесь (t) - рациональная функция, поэтому '(t) - также рациональная функция. Поскольку

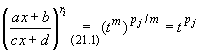dx = '(t)dt,   ,   j = 1, 2, ... n,

то

=

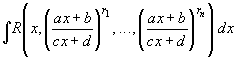где   - рациональная функция. Таким образом, замена переменной (21.1) сводит интеграл

к интегралу от рациональной функции. К рассмотренному типу интегралов относятся интегралы вида

,    a 0,

в частности интегралы .

    Пример. . Сделаем согласно формуле (21.1) замену переменной t² = x, t > 0, откуда dx = 2tdt и, следовательно,

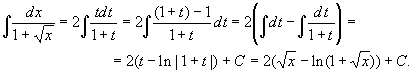
    К интегралам вида (21.3) иногда удается свести интегралы других типов, например, интегралы вида
dx, когда квадратный трехчлен x² + px + q имеет действительные корни. В самом деле, если x² + px + q = (x - a)(x - b), то

== = ,

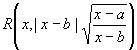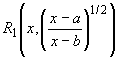где R₁ - рациональная функция. Поэтому

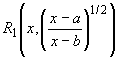dx = dx

и в правой части получился интеграл типа (21.3).

Рациональные функции от функций  Оглавление  Интегралы от дифференциального бинома