;
(21.4)
Рассмотрим интеграл вида
|
(21.4) |
его подынтегральное выражение называется дифференциальным
биномом. Будем рассматривать случаи, когда 
, 
и 
являются
рациональными, а a и b - произвольными
действительными числами. Сделаем в интеграле (21.4)
замену переменной
|
(21.5) |
тогда 
и ,
следовательно,
|
(21.6) |
Таким образом, интеграл (21.4) с помощью подстановки (21.5) сводится к интегралу вида
|
(21.7) |
где и 
- рациональные числа, = ( + 1)/ - 1.
Рассмотрим три случая.
1. - целое
число. Пусть = m/n,
где m и n > 0 - целые числа. Согласно
результатам п. 21.1
подстановка u = t1/n
сводит интеграл (21.7) к интегралу от рациональной
дроби.
2. - целое
число. Пусть теперь = m/n,
где m и n > 0 - целые числа. Тогда
согласно тому же п. 21.1 интеграл (21.7) приводится
к интегралу от рациональной функции с помощью
подстановки u = (a +bt)1/n.
3. + - целое число. Пусть, как
и выше, = m/n, где m
и n > 0 - целые числа. Имеем
= 
.
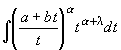Снова получился интеграл типа,
рассмотренного в п. 21.1: подстановка u = [(a +bt)/t]1/n
сводит его к интегралу от рациональной функции.
Итак, в трех случаях, когда , или +
являются целыми числами, интеграл (21.7) сводится к
интегралу от рациональных функций. Поэтому если
хотя бы одно из чисел , ( + 1)/ или ( + 1)/ + в первоначальном интеграле
(21.4) является целым числом, то этот интеграл
сводится к интегралу от рациональных функций и,
следовательно, выражается через элементарные
функции.
Русский математик П.Л. Чебышев показал, что ни в каком
другом случае рациональных показателей ,
и интеграл (21.4)
не выражается через элементарные функции.
.
