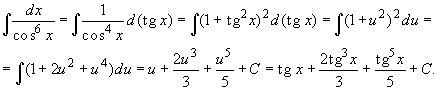Интеграл
сводится подстановкой
x = tg (x/2),
- |
(22.1) |
к интегралу от рациональной функции. Действительно,
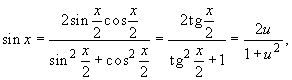
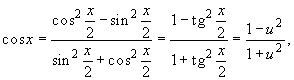
x = 2 arctg u, dx = 2du/(1 + u2),
поэтому
= 
,
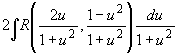т. е. получился интеграл от рациональной
функции.
При вычислении интегралов типа часто оказываются полезными
также и подстановки
u = sin x, u = cos x, u = tg x. |
(22.2) |
В ряде случаев при интегрировании с помощью этих подстановок требуется провести меньше вычислений, чем при интегрировании с помощью подстановки (22.1).
Примеры.
1. Применим
подстановку (22.1) для вычисления интеграла 
Имеем
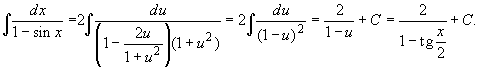
2. Для вычисления интеграла 
применим подстановку u = tg
x:
< x <