22.2. Интегралы 

В случае когда m и n - рациональные числа, интеграл подстановкой u = sin x или v = cos x сводится к интегралу от иррациональной функции, а именно к интегралу от дифференциального бинома (п. 21.3*).
    В самом деле, если, например, u = sin x, то

и, следовательно,

= ,

т. е. действительно получился интеграл от дифференциального бинома и, таким образом, выражается ли он через элементарные функции, зависит от того, какие при этом получились показатели степеней (см. п. 21.3*).
     В случае когда m и n - целые числа, интеграл относится к типу интегралов, рассмотренных в предыдущем пункте, и для его вычисления целесообразно использовать подстановки (22.2).
Например,

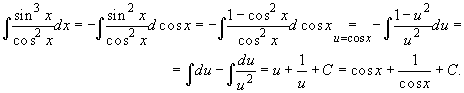
    Если m = 2k + 1 и n = 2l + 1 - нечетные числа, то полезна подстановка t = cos 2x:

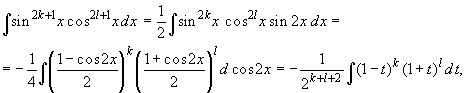
т. е. получился интеграл от рациональной дроби (k и l могут быть отрицательными).
    Если m и n - четные числа, то полезна подстановка u = tg x - см. пример 2 в п. 22.1.
    Если оба показателя m и n неотрицательные и четные, то, применив формулы sin² x = (1 - cos 2x)/2,   cos² x = (1 + cos 2x)/2, олучим интеграл того же типа, но с меньшими показателями, например,

    Отметим, что методами, аналогичными методам, описанным в этом пункте, берутся интегралы вида
sh^m x chⁿ x dx.

ИнтегралыОглавление Интегралы,,