, 
, 
, 
, 
, 
, 
, 
, 
, 
.К интегралам от трансцендентных функций, вычисляющимся с помощью интегрирования по частям, относится много разнообразных интегралов, например,
, , , , ,
, , , , .
Здесь везде n - целое неотрицательное
число. Для вычисления интегралов и следует их дважды
проинтегрировать по частям, в результате для
каждого из них получится линейное уравнение, из
которого они сразу находятся. Например,
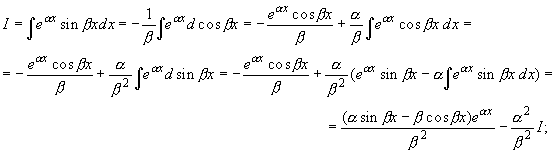
отсюда 
В интегралах , , после
однократного интегрирования по частям
получаются интегралы тех же типов, но с меньшими
показателями степени.
Рассмотрим пример:
xsin x dx
= -x dcos x =
-x cos x + cos x dx = -x cos
x + sin x + C.
В интегралах ,
, , , в
результате однократного интегрирования по
частям пропадает трансцендентная функция,
причем в первых двух получаются интегралы от
иррациональных функций, выражающиеся через
элементарные функции, а в трех последних -
интегралы от рациональных функций и,
следовательно, также выражающиеся через
элементарные функции. Например,
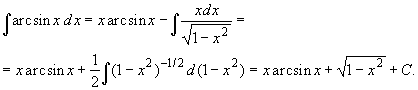
В заключение подчеркнем, что далеко
не всякий интеграл от элементарной функции
выражается через элементарные функции. Среди
таких интегралов встречаются интегралы, которые
находят большое применение в различных разделах
математики. К числу их относятся, например,
вероятностный интеграл 
,
интегральный логарифм 
,
интегральный синус 
.
,
,