23.2. Ограниченность интегрируемых функций

    Изучение определенного интеграла начнем с исследования необходимых, а затем и достаточных условий интегрируемости функций.
    Теорема1. Если функция интегрируема на некотором отрезке, то она ограничена на нем.
Пусть функция f интегрируема на отрезке [a,b] и = I .
    Зафиксируем какое-либо > 0, например = 1. Согласно определению 2 интеграла существует такое > 0, что для любой интегральной суммы , соответствующей разбиению мелкости || < , выполняется неравенство | - I| < 1 , а следовательно, и неравенство

т. е. множество {} значений интегральных сумм , || < , функции f ограничено.
    Допустим теперь, что существует функция f, интегрируемая на некотором отрезке [a,b], и неограниченная на этом отрезке. Возьмем произвольное разбиение отрезка [a,b]. Из того, что функция f неограниченна на отрезке [a,b], следует, что она неограниченна и по крайней мере на одном из отрезков разбиения . Пусть для определенности функция f неограниченна на отрезке [x₀,x₁]. Из ее неограниченности на этом отрезке следует, что для любого числа n на нем существует такая точка, обозначим ее , что

| f()| > n,     [x₀,x₁],     n = 1, 2, ...

Отсюда, очевидно, следует, что

Зафиксируем какие-либо точки _k в остальных отрезках разбиения :

 _k [x_k-1,x_k],      k = 2, 3, ..., .

Тогда сумма

будет иметь вполне определенное значение. Добавив к этой сумме слагаемое f()x₁ , получим интегральную сумму , причем в силу условия (23.3) и постоянства суммы (23.4) будем иметь

= [f()x₁ + ] = .

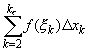а следовательно, для любого разбиения множество значений интегральных сумм неограниченно. Поэтому неограниченно и множество {}, || < (число > 0 было выбрано выше), что противоречит неравенству (23.2). 
    Замечание. Условие ограниченности функции, являясь необходимым условием интегрируемости функции по Риману, не является достаточным условием для этого. В самом деле, рассмотрим, например, функцию Дирихле

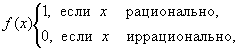
Каковы бы ни были отрезок [a,b] и его разбиение , выбрав все точки _k [x_k-1,x_k] рациональными, в силу условия , f(_k) = 1, получим

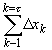= = b - a,

а выбрав точки _k иррациональными, в силу условия f(_k) = 0, k = 1, 2, ..., , будем иметь

=

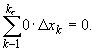
Поэтому интегральные суммы функции Дирихле заведомо не имеют предела при ||0.
    Тем самым функция Дирихле дает пример функции, ограниченной на любом отрезке, но неинтегрируемой на нем.

Определенный интеграл Римана  Оглавление Верхние и нижние суммы Дарбу